Метод наименьших квадратов

При проведении эксперимента часто измеряют пары величин х и у, причем одна из них является функцией другой величины, например, у = f(х). Затем найденные значения наносят в виде точек на координатную плоскость и пытаются найти кривую, соответствующую алгебраической функции у = f(х), которая проходила бы как можно ближе к точкам. Из теории вероятностей следует, что наилучшим приближением будет такая зависимость, для которой сумма квадратов расстояний по вертикали от каждой экспериментальной точки до кривой будет минимальной.

Ограничимся рассмотрением случая линейной зависимости y = kx + b. Линейная зависимость очень широко распространена в физике. И даже когда зависимость нелинейная, можно выбрать величины, откладываемые по осям, таким образом, чтобы график рассматриваемой зависимости являлся прямой линией. Например, график зависимости пути от времени при равноускоренном движении строят в осях S = f(t²), график зависимости частоты собственных колебаний струны от ее натяжения (F) – в осях ν = f(F^1/2), график зависимости энергетической светимости тела от его температуры (Т) – в осях R_e = f(T⁴).

Рассмотрим математическую сторону вопроса о нахождении наилучших значений углового коэффициента k и параметра b. При выводе предположим, что ошибки содержат только значения у_i (такое предположение часто оправдывается на практике), иначе анализ весьма усложнится. Отклонение экспериментального значения у_i от искомой линейной зависимости в i-м измерении, то есть при х = х_i, составит:

(11)

Наилучшие значения k и b выбираются таким образом, чтобы сумма квадратов этих отклонений по всем n измерениям

(12)

была минимальной (отсюда и название – метод наименьших квадратов). Для определения значений kиb, при которых величинаSминимальна, приравниваем к нулю частные производные отSпоkиb:

(13)

(14)

Искомые величины kиbполучаются решением системы уравнений:

(15)

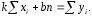(16)

(n– число измеренийx_i иy_i).

Второе уравнение показывает, что наилучшая прямая проходит через точку с координатами:

(17)

Из уравнений (15)-(16) находим угловой коэффициент kи параметрb:

(18)

(19)

Мера качества приближения – средние квадратичные отклонения величин kиb:

(20)

(21)

(22)

Очевидно, что ручная обработка результатов с помощью приведенных формул достаточно трудоемка. Однако применение компьютеров при обработке данных лабораторных исследований позволяет использовать этот достаточно мощный метод. В программах к некоторым лабораторным работам применение метода наименьших квадратов позволяет строить графические зависимости и находить искомые значения параметров с повышенной точностью.

Оформление отчетов по лабораторным работам

Отчет по лабораторной работе должен содержать следующие разделы:

1. Номер лабораторной работы.

2. Название работы.

3. Цель работы (из методических указаний).

4. Краткая теория, включая ответы на контрольные вопросы.

5. Схема и описание установки.

6. Экспериментальные результаты (форма таблицы и конкретный порядок выполнения работы устанавливаются преподавателем).

7. Результаты обработки с подробными примерами расчёта искомых величин и их погрешностей.

8. Графики (при необходимости).

9. Выводы.

Выводы должны соответствовать поставленной цели работы (например, если в цели работы указано – проверить выполнение закона, то в выводах дается объяснение, каким образом в данной работе подтверждён этот закон).