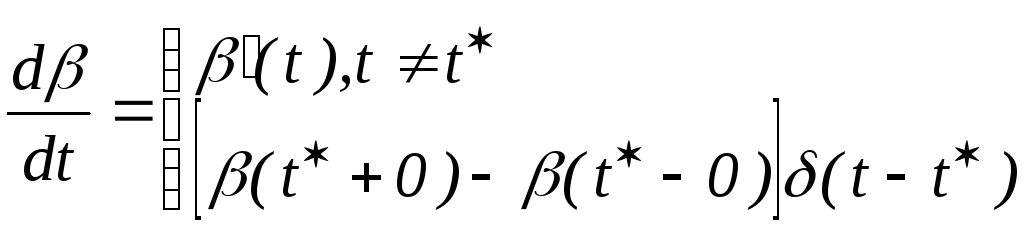Лекция 10 План лекции

1. Единичная ступенчатая функция.

2. Дельта - функция.

3. Два способа введения -функции.

4. Фильтрующее свойство -функции.

Некоторые специальные функции.

1. Единичная ступенчатая функция.

Единичной ступенчатой функцией (1(t)) называют следующую функцию:

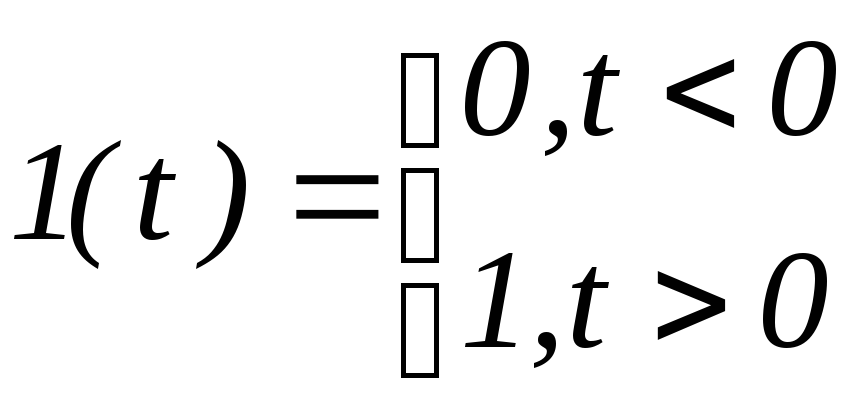(1)

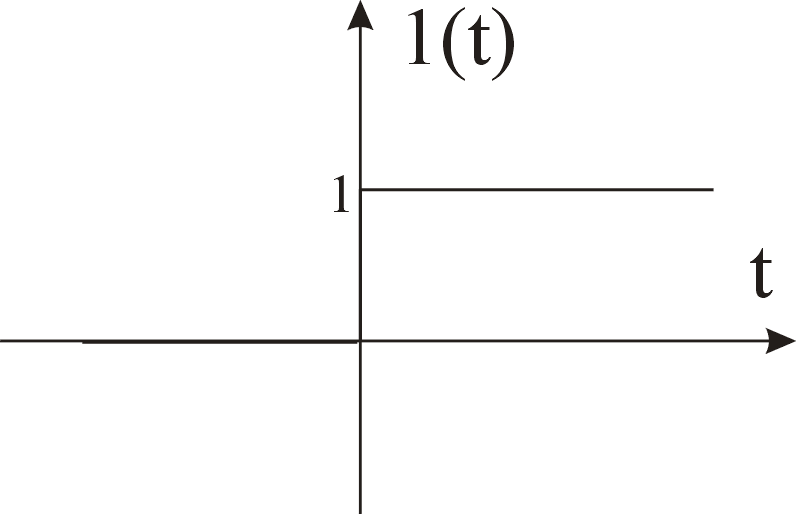рис. 1

Равенство (1) не определяет значение функции 1(t) в момент t=0. В большинстве случаев это обстоятельство не имеет никакой роли. При необходимости функцию 1(t) доопределяют одним из трех способов.

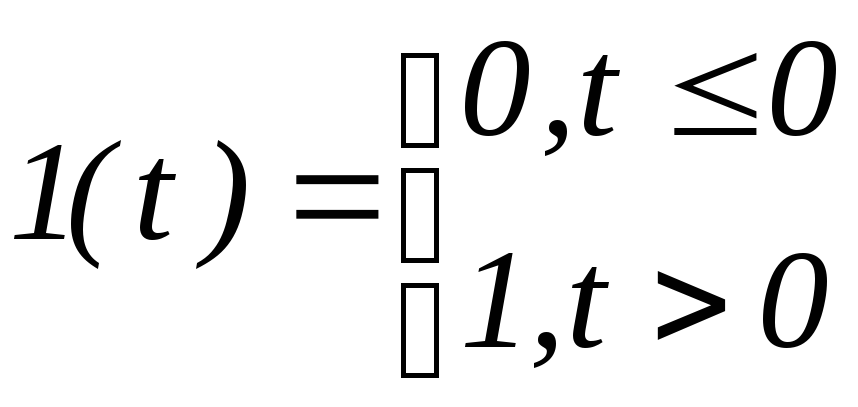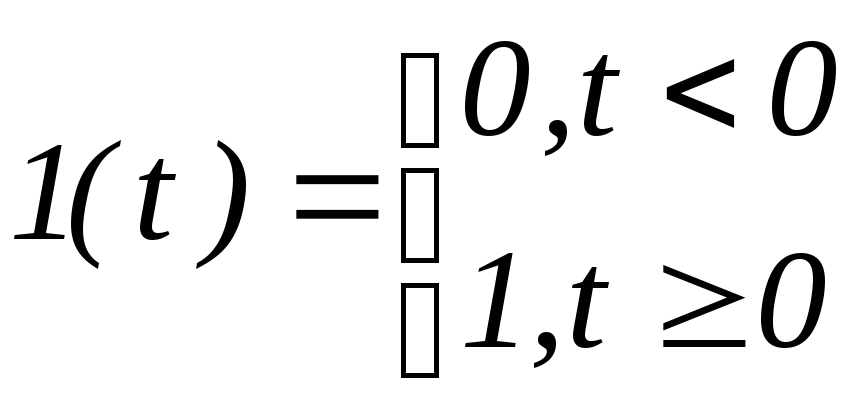1) 2)3)

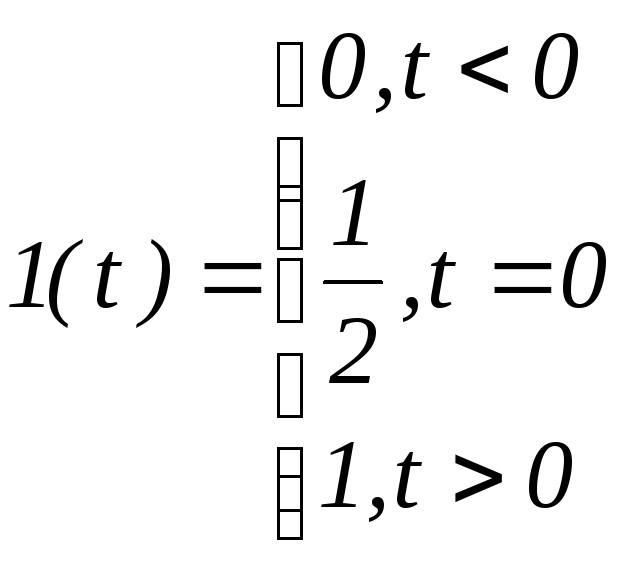
Запаздывающая единичная ступенчатая функция задается соотношением:

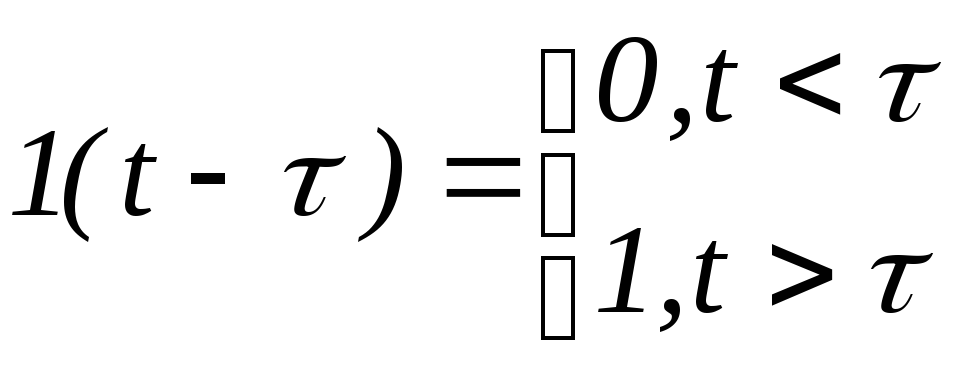
Название запаздывающая функция обосновано тем, что график функции получается из графика 1(t) путем смещения вправо на величину.

Функции вида - запаздывающие, т. к. они повторяют сигналf(t), но с запаздыванием на величину времени , т. е. со смещением графика функции вправо.

Р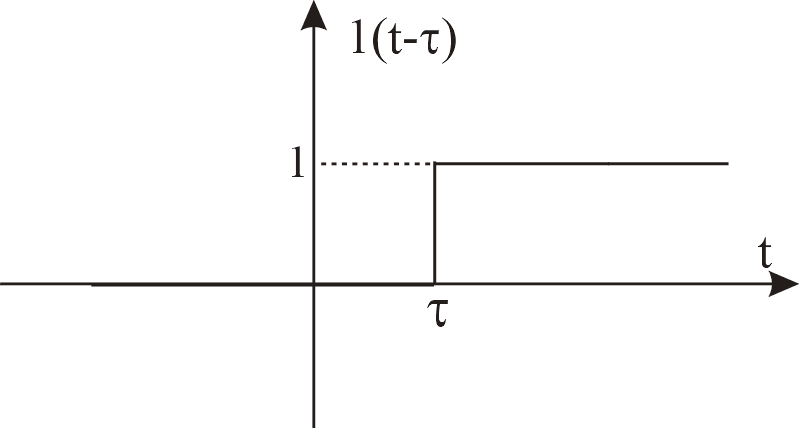ис. 2

2. Дельта функция.

Дельта функция () введена в математику известным физиком Дираком и поэтому часто называется функцией Дирака. Дельта функция не является функцией в обычном смысле слова, а относится к так называемым обобщенным функциям.

Существуют разные способы введения  - функции.

 - функцией будем называть функцию, удовлетворяющую следующему интегральному уравнению: (2)

Проанализируем уравнение (2).

Из (2) следует, что при t<0 (3)

Поскольку соотношение (3) справедливо для любого t<0, то это очевидно возможно лишь при условии (t)=0 при t<0.

Пусть t>0. Обозначим через  малое положительное число. Запишем равенство:

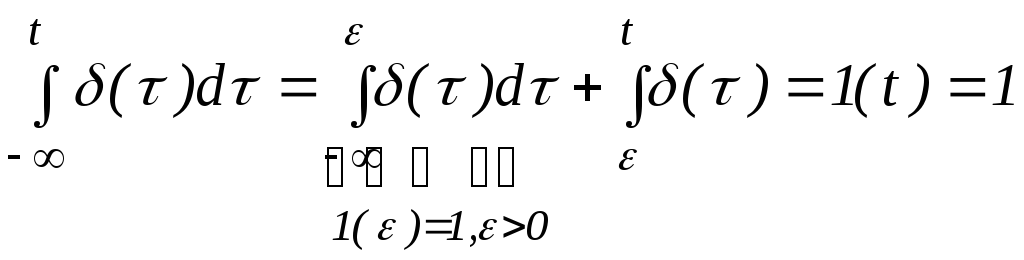(4)

Из (4) следует равенство:

(5)

Так как равенство (5) справедливо для любого t>, то это возможно только при условии (t)=0 при t>.  - cколь угодно малое положительное число, поэтому справедливо равенство: (t)=0 при t>0.

Для определения значения функции в момент времени t=0 в соответствии с (2) запишем

, где  - малое положительное число.

В соответствии с (2) .

(6)

Равенство (6) справедливо для любого сколь угодно малого положительного . Таким образом, площадь под кривой на бесконечно малом интервале интегрирования равняется положительному числу 1. Это возможно только при условии . Следовательно

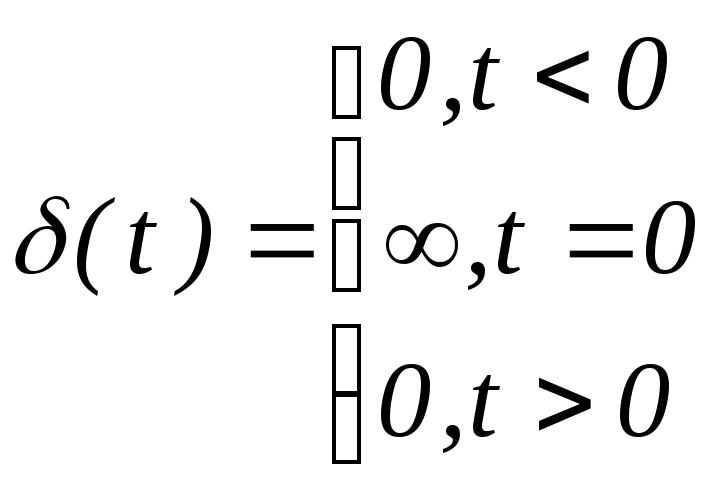(7)

К равенству (7) необходимо добавить соотношение (8),

которое непосредственно следует из равенства (2).

 - функцию обычно задают с помощью соотношений (7) и (8). Продифференцируем формально по tравенство (2).

На этом основании (t) рассматривают как производную единичной ступенчатой функции.

Соотношение между 1(t) и(t) пояснить с помощью следующих предельных переходов. Рассмотрим функцию. Покажем, что. Действительно

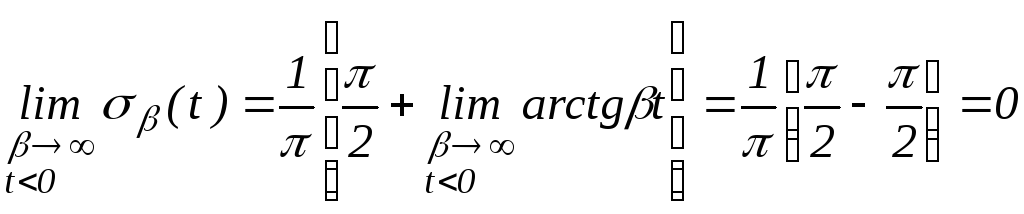
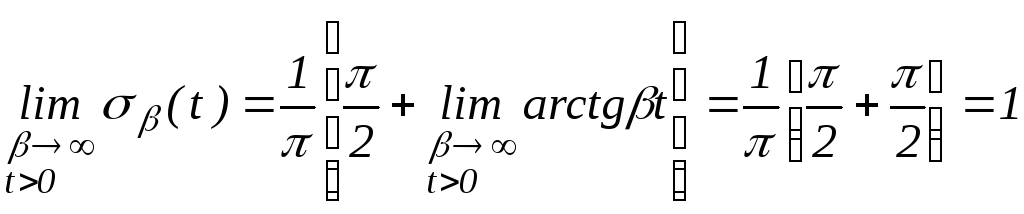
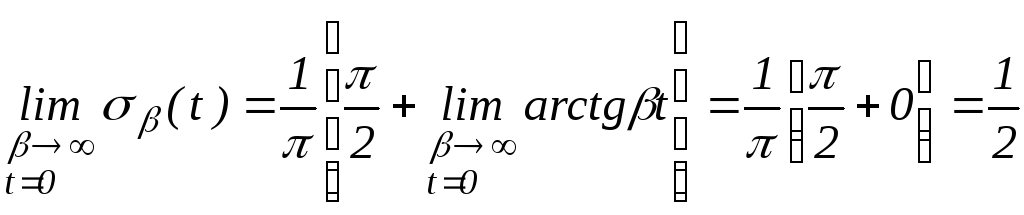
р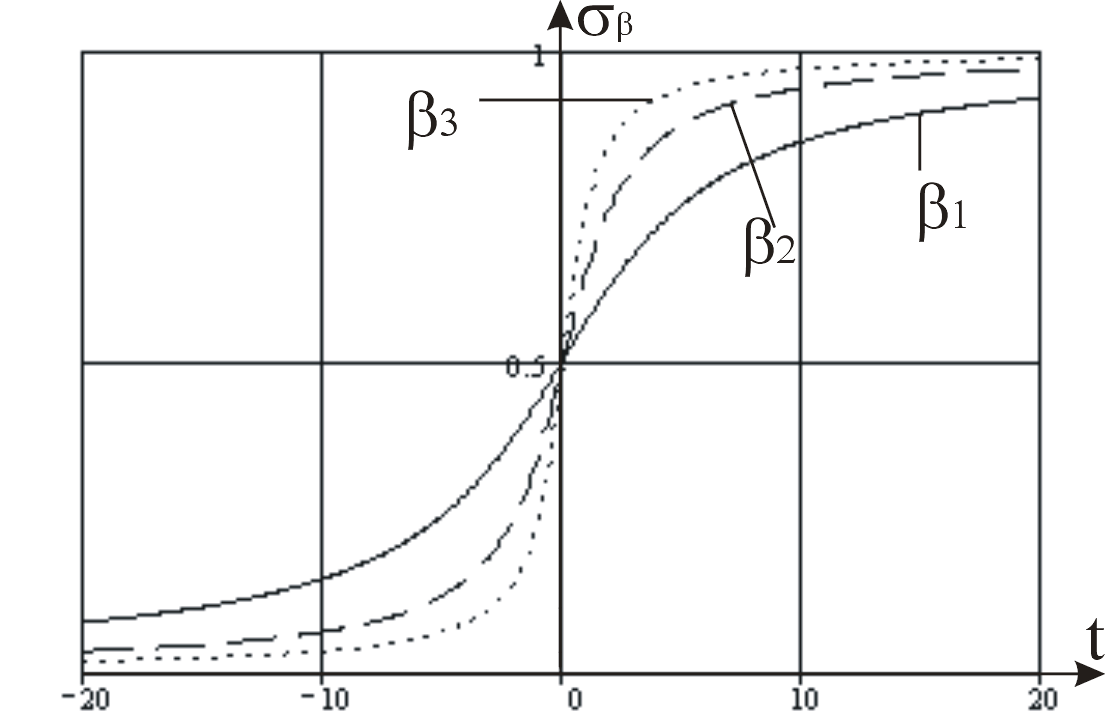ис. 3 ()

Найдем производную .

Покажем, что . Действительно

.

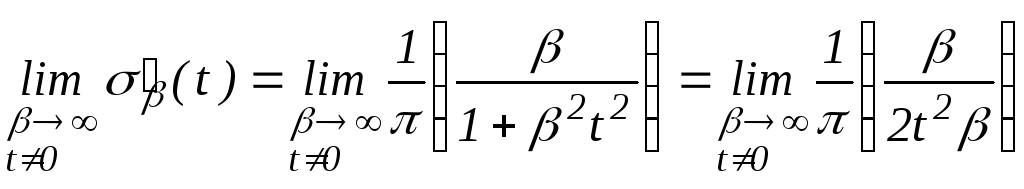
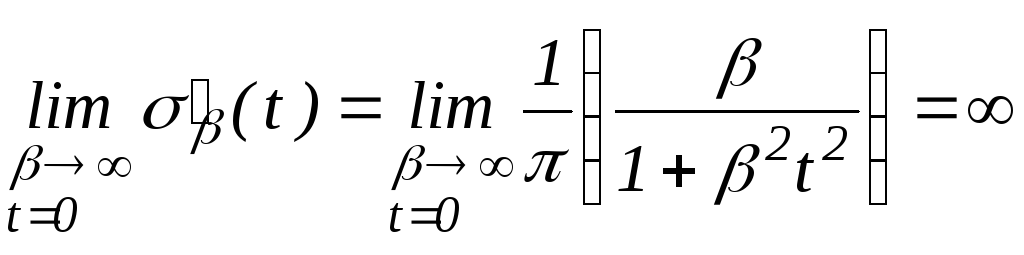
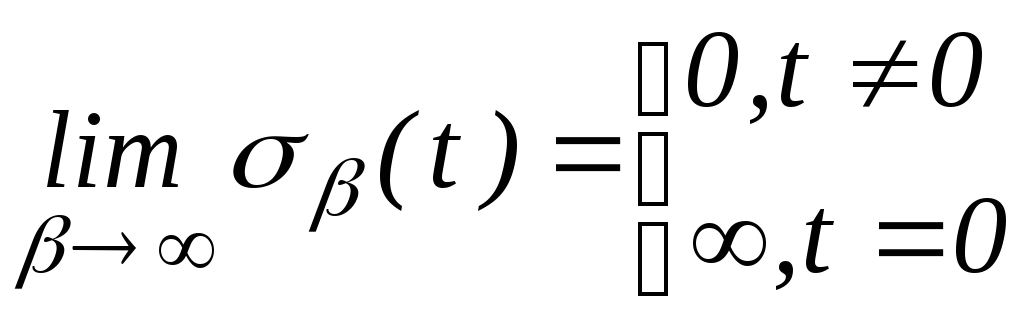
, ч. т. д.

На основании ,. Заключаем

.

Р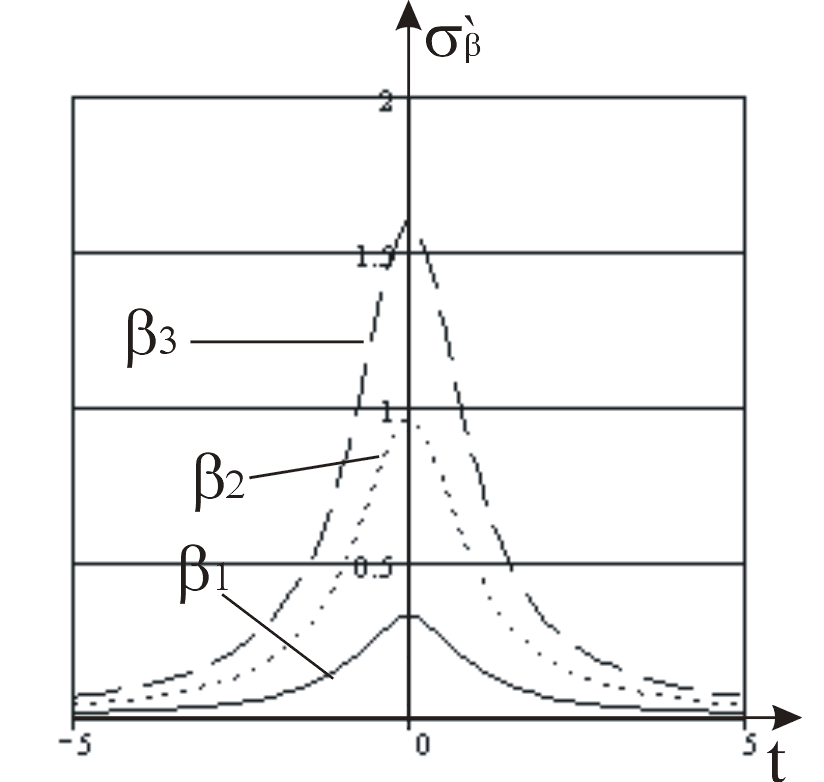ис. 4()

Запаздывающая - функция определяется соотношением

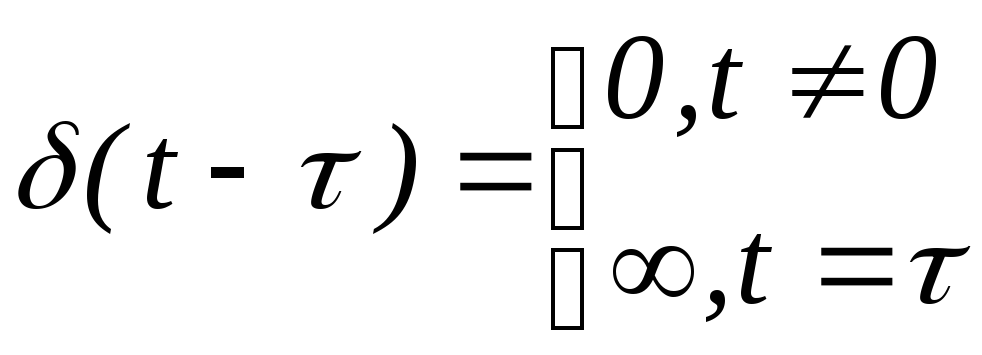
Рассмотрим интеграл , полагая, чтоf(t)непрерывна в точке. Принимая во внимание вид(t), имеем

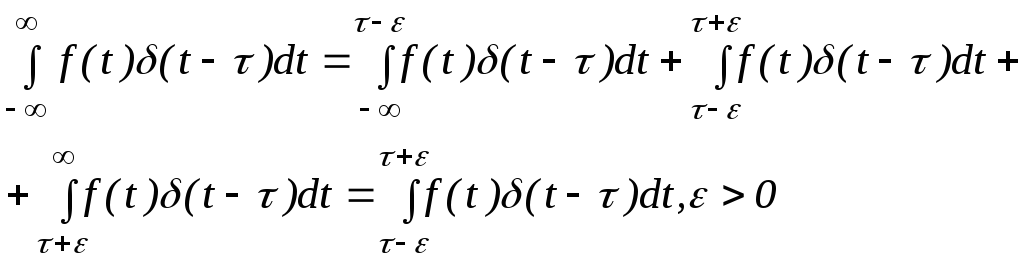(9)

.

Свойство, выраженное равенством называют фильтрующим свойством(t).

Введение - функции позволяет дифференцировать разрывные функции. Рассмотрим функцию, которая имеет в точкеразрыв первого рода.

при