Лекция 7 План лекции

1. Ряд Тейлора.

2. Ряд Лорана.

3. Типы особых точек.

4. Особые точки и вид ряда Лорана.

5. Понятие вычета.

Представление аналитических функций рядами.

1. Ряд Тейлора.

Теорема 10. Если функция f(z) аналитична в круге , то она в этом круге может быть представлена рядом Тейлора:

, где - коэффициент ряда разложения.

, где n=0, 1, 2…

В любой замкнутой области, принадлежащей этому открытому кругу, ряд Тейлора сходится равномерно.

Точка а – центр разложения, R – радиус сходимости.

2. Ряд Лорана.

Будем предполагать, что функция f(z) аналитична в кольце К: .

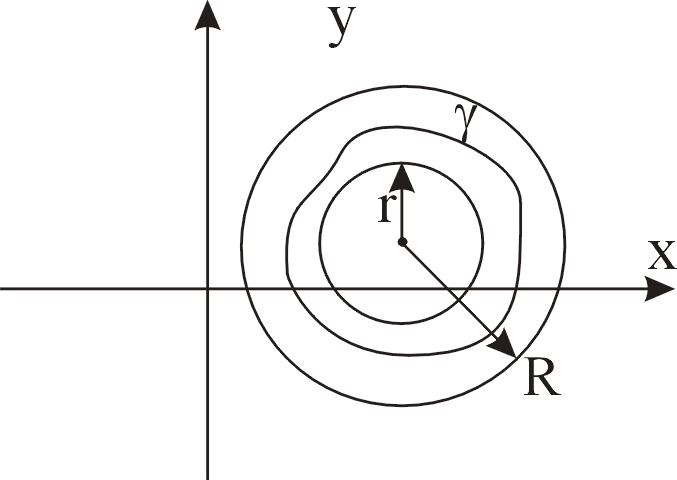
Рис. 1

Теорема 11. Если функция f(z) аналитична в кольце К, то она в этом кольце может быть представлена рядом Лорана:

, где

- любой замкнутый контур, лежащий целиком в кольце К и охватывающий точку а, которая является центром разложения.

Ряд Лорана можно получить, расширяя ряд Тейлора в область отрицательных значений n, n <0.

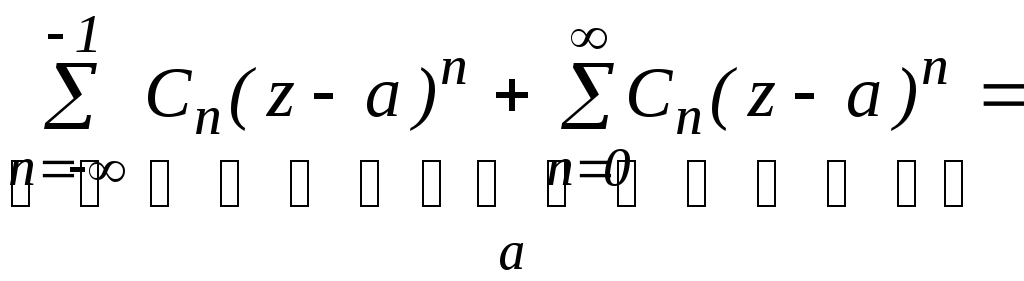
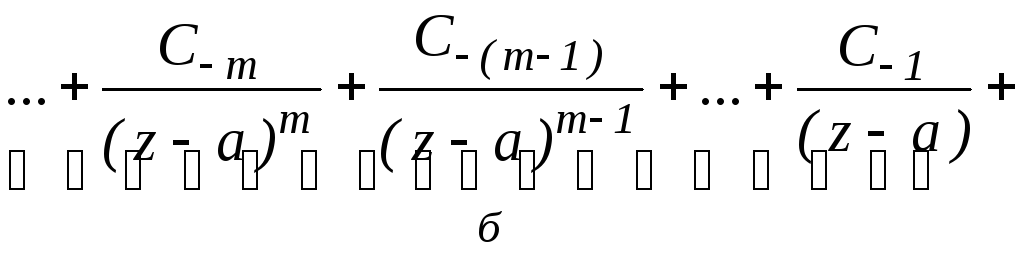
Сумма членов ряда Лорана, содержащих отрицательные степени называютсяглавной частью ряда Лорана. Сумма членов ряда Лорана, содержащих положительные степени называется правильной частью ряда Лорана.

Ряд Лорана (а) сходится в области, в которой сходятся ряды (б) и (в). Пусть ряд Тейлора сходится в круге , ряд (б) сходится вне круга

, тогда если r>R, то ряд Лорана расходится, если r<R, то сходится в кольце К.

Пример.

Рассмотрим разложение функции f(z).

. Выберем в качестве центра разложения точку z=0.

1) Функция f(z) аналитична в круге . В соответствии с теоремой 10 она может быть представлена рядом Тейлора:.

Р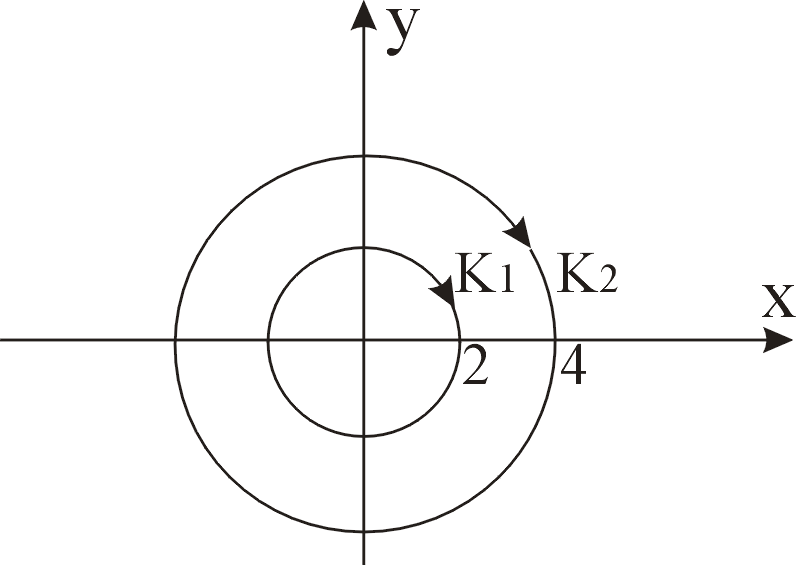ис. 2

2) Функция f(z) аналитична в кольце . По теореме 11 она может быть представлена рядом Лорана:

,

3) Функция f(z) аналитична в кольце . По теореме 11 она может быть представлена рядом Лорана:

,

ОСОБЫЕ ТОЧКИ И ВИД РЯДА ЛОРАНА.

Точка а называется изолированной особой точкой функции f(z), если найдется окрестность точки а, в которой функцияf(z) аналитична и аналитичность нарушается при переходе к самой точке.

Более точное определение:

Точка а называется изолированной особой точкой функции f(z), если найдется кольцо К, вида , в котором функцияf(z) аналитична и аналитичность не имеет места в самой точке.

Различают три типа изолированных особых точек:

1. изолированная особая точка а называется устранимой, если существует.

Пример.

z=0 – устранимая изолированная особая точка функции , т. к.

Название устранимая особая точка оправдывается тем, что особенность функции в этой точке можно устранить, если положить

2. изолированная особая точка а называется полюсом, если функцияf(z) неограниченно возрастает при.

Пример.

z=3 – полюс точка функции .

Каждый полюс а функции f(z) является нулем а функции .

Порядком полюса а функции f(z) называют порядок нуля а функции

Говорят, что точка а является нулем функции порядкаm, если .

Пример.

z=3 – полюс третьего порядка функции .

3. изолированная особая точка а называется существенно особой, если не существует .

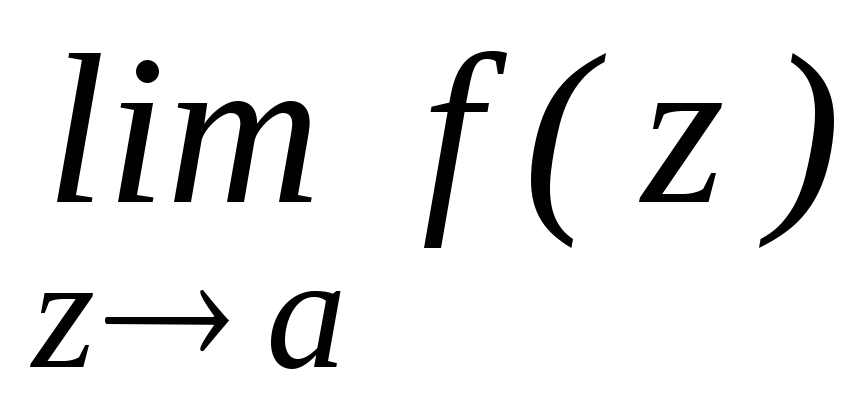Пример.

z=0 - существенно особая точка функции

рис. 1

По определению изолированной особой точки существует кольцо

К: , в котором функцияf(z) аналитична. Разложим функцию f(z) в этом кольце в ряд Лорана:

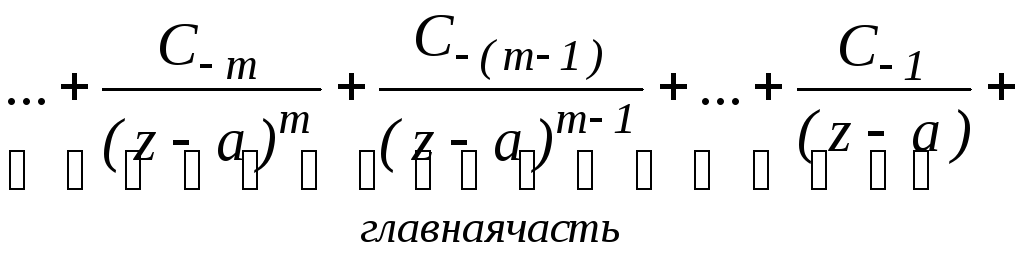
Сумма членов ряда Лорана, содержащих отрицательные степени называютсяглавной частью ряда Лорана. Сумма членов ряда Лорана, содержащих положительные степени называется правильной частью ряда Лорана.

Могут иметь место три случая:

1. ряд Лорана содержит только правильную часть

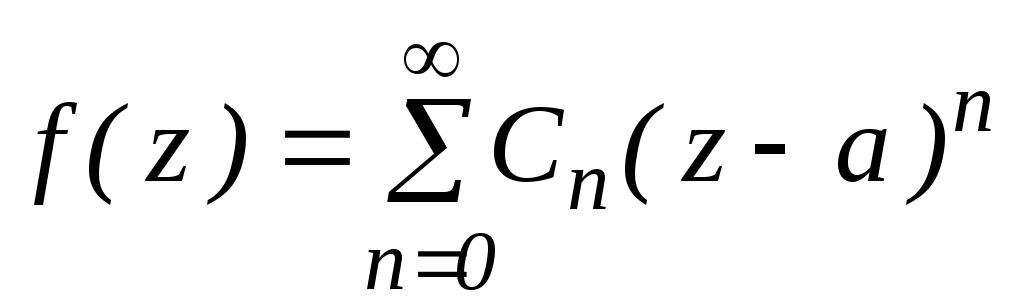
Тогда , т. е. точка а –устранимая особая точка.

2. ряд Лорана содержит конечную главную часть

Представим:

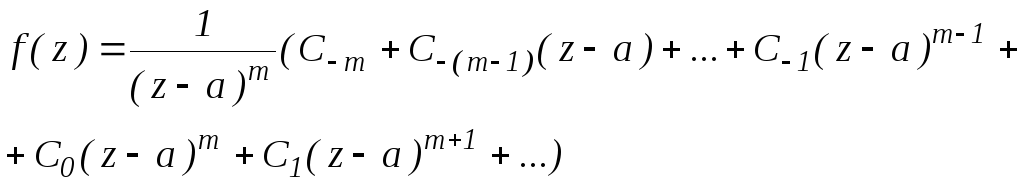
Можно видеть, что

Точка а – является полюсом функции f(z). В ТФКП, доказывается, что порядок полюса совпадает с числом членов в главной части ряда Лорана.

3. ряд Лорана содержит бесконечную главную часть

В ТФКП, доказывается, что точка а– является существенно особой точкой функции f(z).

Пусть точка а –изолированная особая точка функции f(z). По определению существует кольцо К: , в котором функцияf(z) аналитична. Разложим функцию f(z) в этом кольце в ряд Лорана по степеням . В этом разложении особую роль играет коэффициент,(коэффициент при сомножителе), который называетсявычетом функции f(z) в точке z=a и обозначается Res

ЛЕКЦИЯ 8

План лекции

1. Теорема о вычетах.

2. Основные формулы вычета в полюсе.

3. Примеры на применение теоремы о вычетах.

ТЕОРЕМА О ВЫЧЕТАХ.

Пусть точка а –изолированная особая точка функции f(z). По определению существует кольцо К: , в котором функцияf(z) аналитична. Разложим функцию f(z) в этом кольце в ряд Лорана: (1)

Обозначим замкнутый контур целиком лежащий в кольце К и охватывает точку а. Вычислим интеграл:

Рассмотрим интеграл . Выделим три случая:

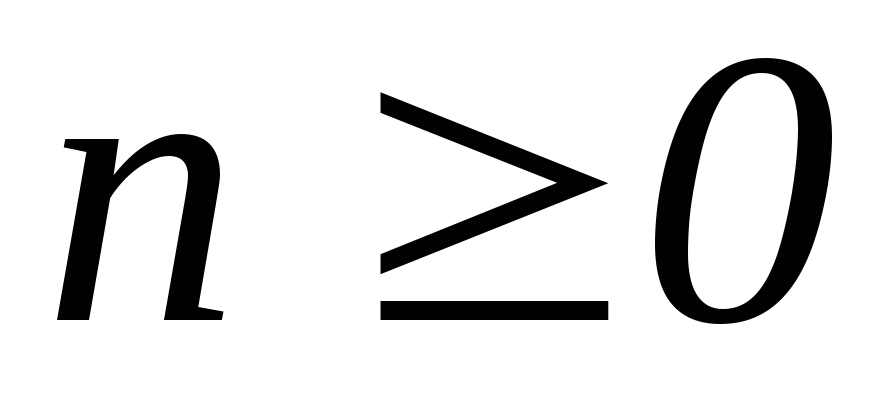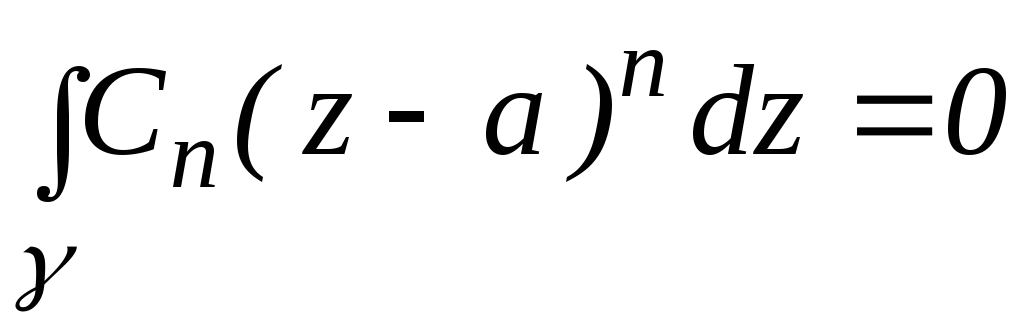1. , (по теореме 7)

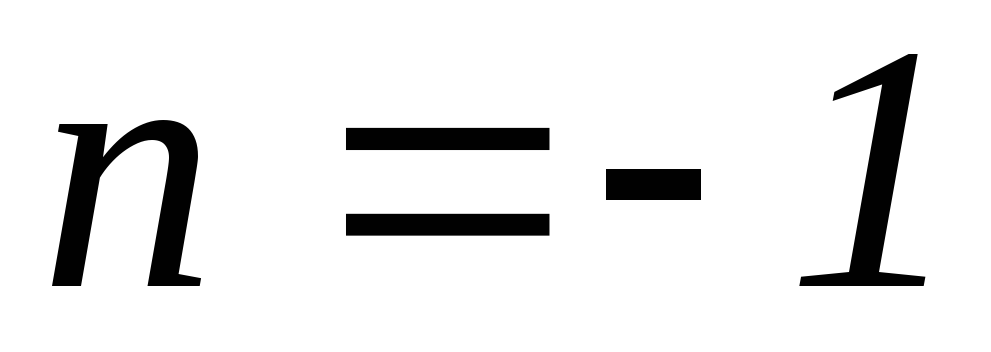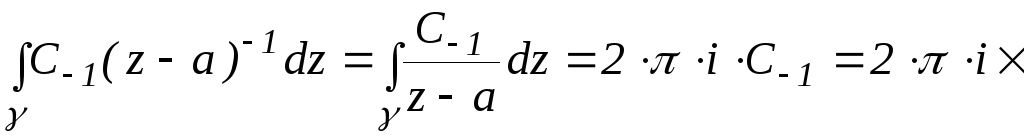
2. , Res.

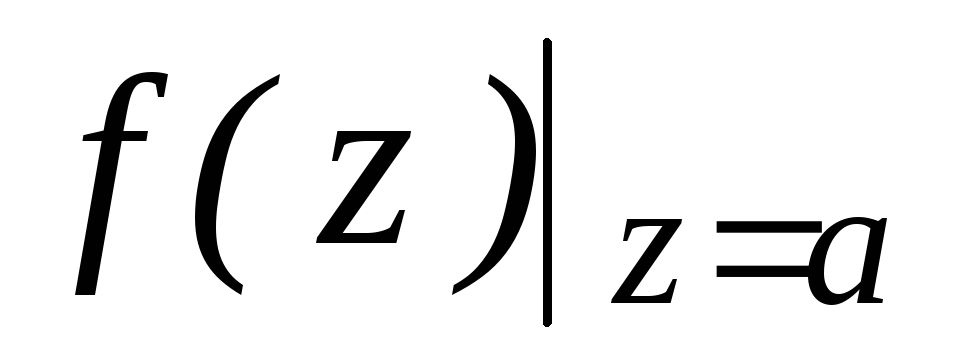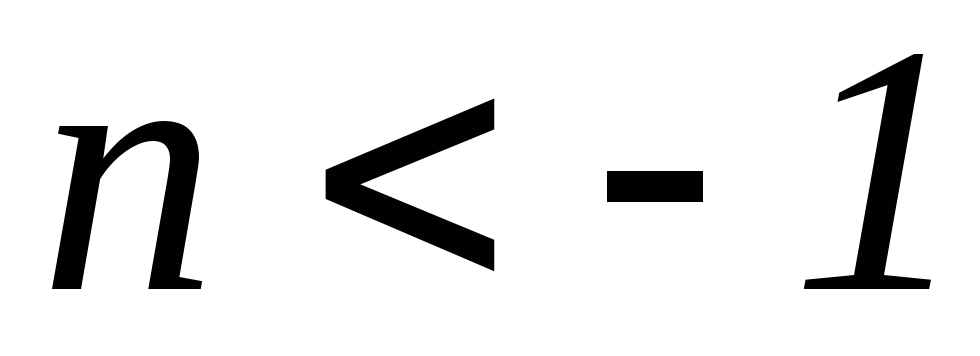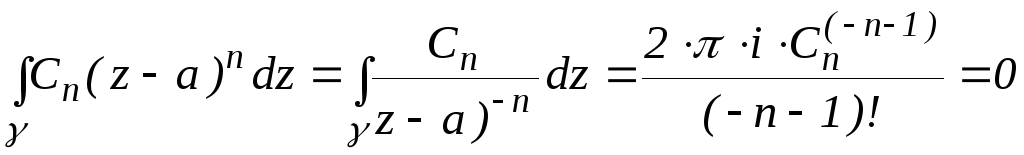3. , (по формуле Коши для высших производных)

Пояснение: формула Коши для высших производных

Заменим в формуле Коши на z, z на а

Получили равенство: Res(2)

Теорема 12.(теорема о вычетах)Если функцияf(z)аналитична в односвязной областиDза исключением конечного числа изолированных особых точеки непрерывна на границе c одластиD, то

Res

Доказательство:

В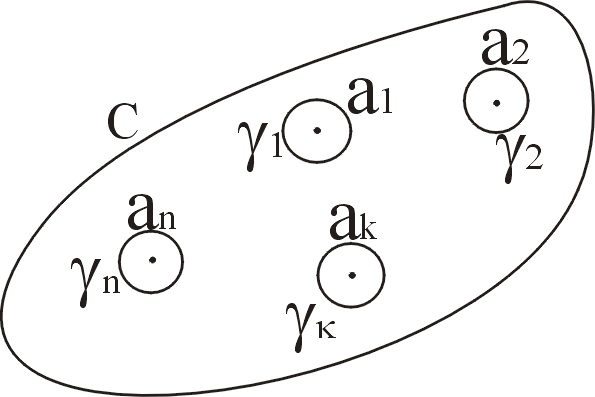ыделим особые точкииз области D с помощью замкнутых контуров . Контура выбираются таким образом, чтобы они не пересекались друг с другом и контуром с.

Рис. 1

Получим (n+1) связанную область, ограниченную с и (к=1, 2,…n), в которых функция f(z) аналитична. По теореме 9: (3).

В соответствии с равенством (2): 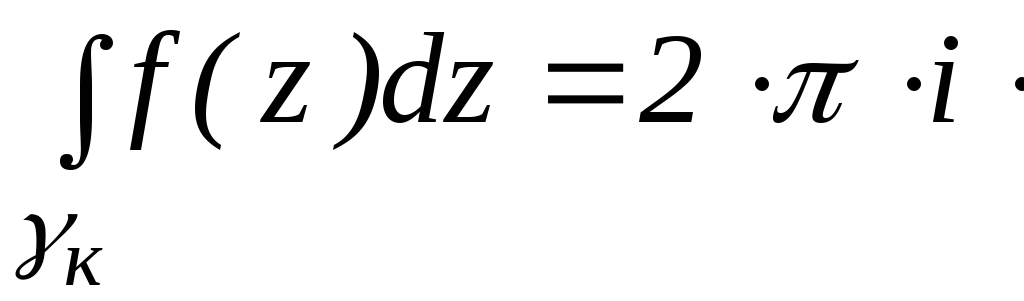Res (4)

Подставляя (4) в (3), получим: Res.

ОСНОВНЫЕ ФОРМУЛЫ ВЫЧЕТОВ В ПОЛЮСЕ.

1. Найдем вычет Res, полагая, что функция f(z) аналитична в точке а. Обозначим через с замкнутый контур, целиком лежащий в области аналитичности функции f(z) и охватывающий точку а. По теореме о вычетах:

Res

По формуле Коши:

Из сравнения полученных результатов следует Res

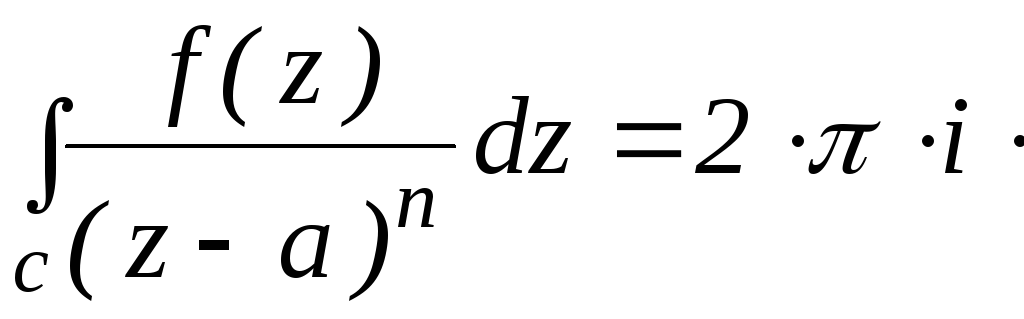2. Найдем Res , полагая, что функция f(z) аналитична в точке а. По теореме о вычетах: Res

С другой стороны по формуле Коши для производных:

Из сравнения полученных формул следует

Res

3. Общая формула вычета в полюсе первого порядка.

Пусть а – полюс первого порядка функции f(z). По определению существует кольцо К: , в котором функцияf(z) аналитична. Разложим функцию f(z) в этом кольце в ряд Лорана:

Перейдем к пределу при в последнем выражении:

Res

Res

4. Найдем Res, полагая, что

При выписанных условиях точка а является полюсом первого порядка функции . Воспользуемся полученным в предыдущем пунктевыражением.

Res

. Получим формулу

Resпри

5. Общая формула вычета в полюсе порядка m.

Пусть а – полюс порядка m функции f(z). Выпишем соответствующий этому полюсу ряд Лорана:

Продифференцируем последнее выражение (m-1) раз

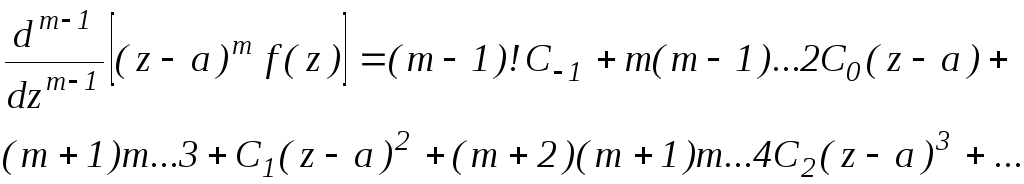
Перейдем к пределу

Res

Получим следующие формулы вычетов в полюсе

Res

Res

Res,

Res (Общая формула вычета в полюсе первого порядка)

Res(Общая формула вычета в полюсе порядка m)

Пример 1.

, с:

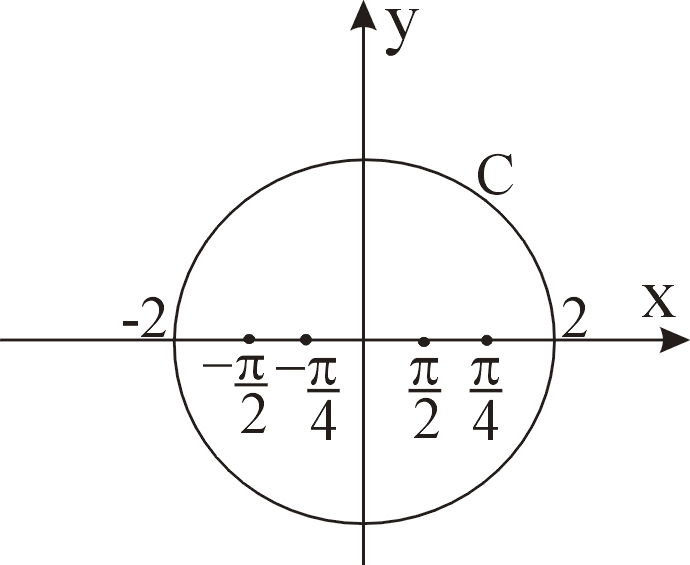рис. 1

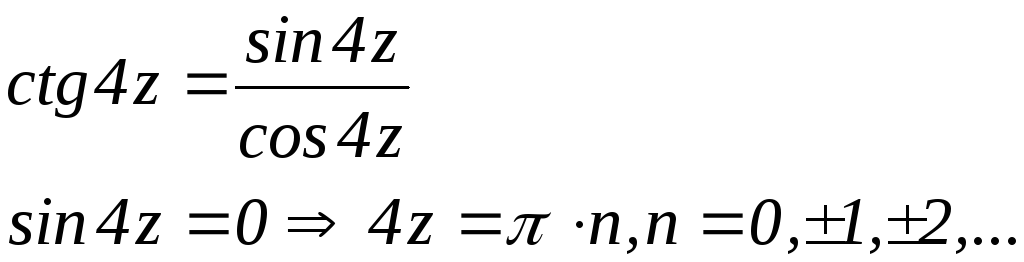
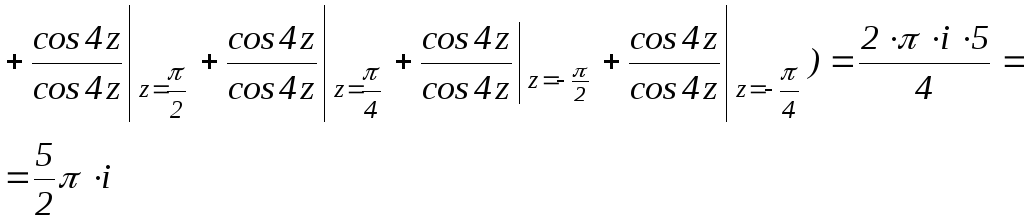
(3 формула вычета)

Пример 2.

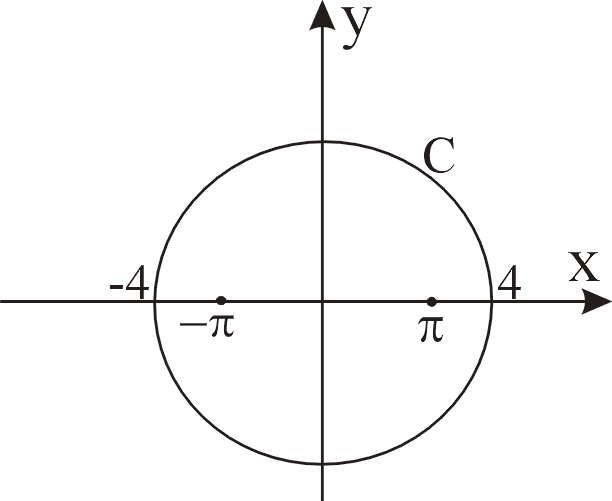, с:

рис. 2

- являются полюсами первого порядка.

Правило определения порядка полюса: нужно из порядка нуля знаменателя вычесть порядок нуля числителя.

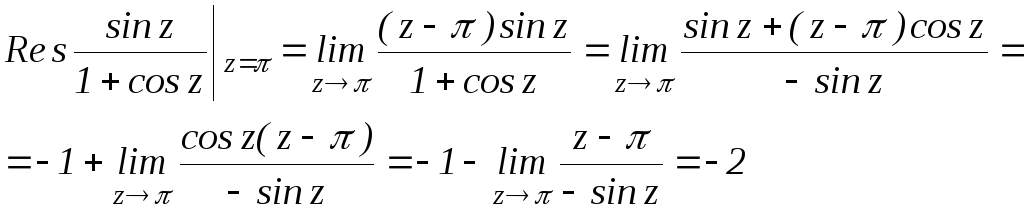
Аналогичным образом легко показать, что , поэтому