Лекция 3 План лекции

1. Показательная функция.

2. Логарифмическая функция.

3. Тригонометрические функции.

4. Гиперболические функции.

5. Обратные тригонометрические функции.

Элементарные функции комплексного переменного.

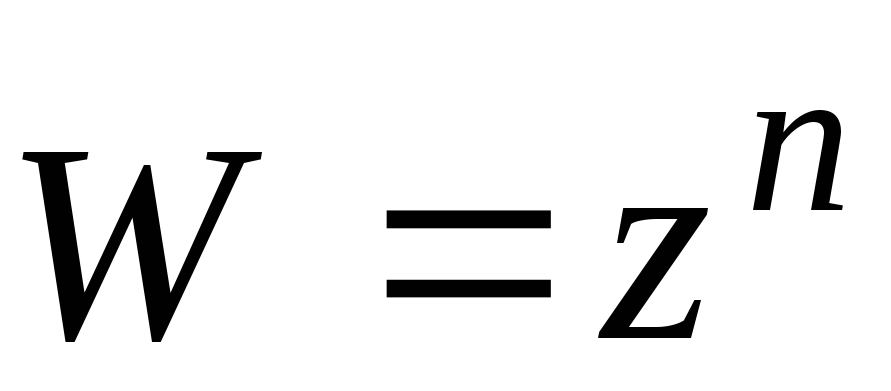1. -эта функция является аналитической на всей комплексной плоскости. По определению:

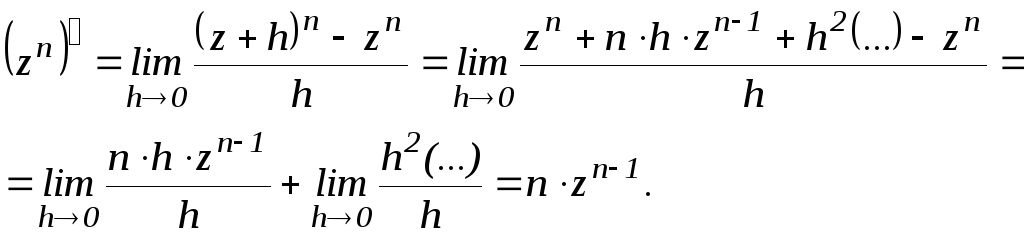
2. Показательная функция .

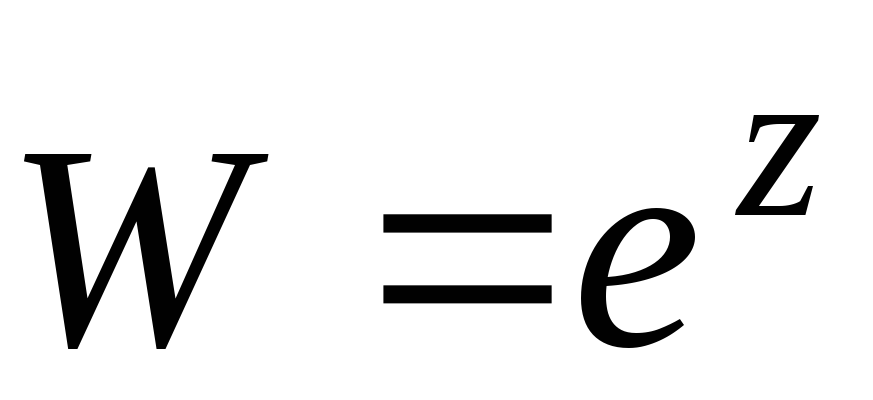Зададим ее равенством . Из равенства следует, что на множестве вещественных чисел показательная функция определяется обычным образом. Рассмотрим произведения:

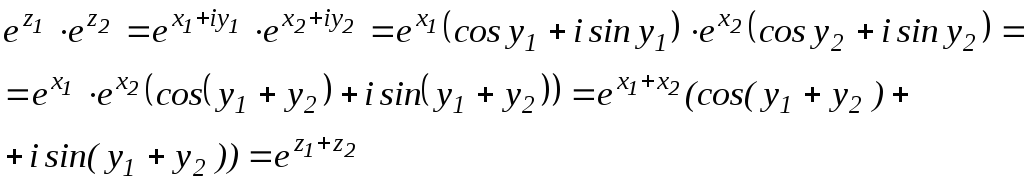При перемножении показательных функций их показатели складываются. Функция является аналитической функцией на всей комплексной плоскости. Проверим условия Коши –Римана:

, где ,

.

, .

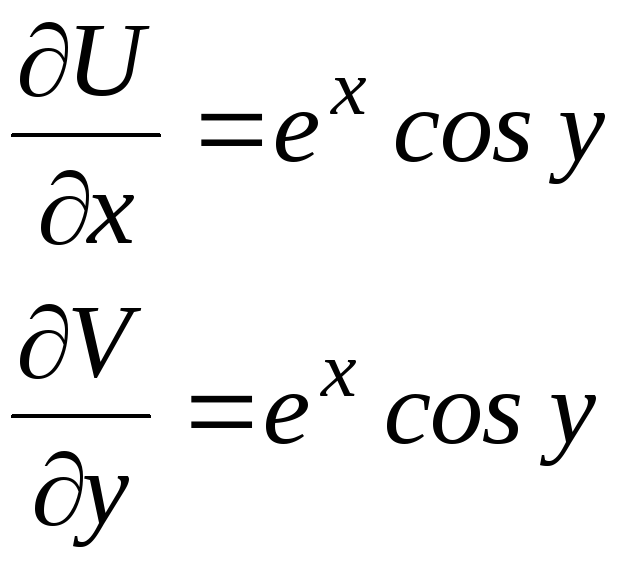
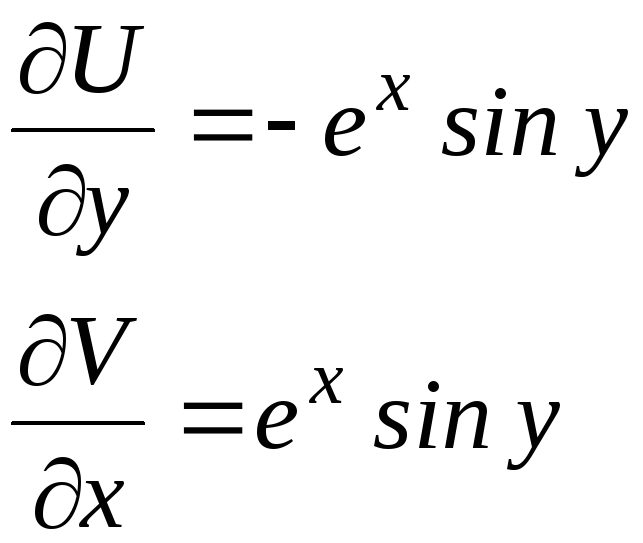
Условия Коши-Римана выполняются в каждой точке плоскости z. Воспользуемся .

.

Положим z=iy. Из определения следует: - формула Эйлера. С помощью формулы Эйлера любое комплексное число можно задать в показательной форме. В соответствии с тригонометрической формой записи:

- показательная форма записи комплексного числа.

Функция - является периодической функцией с чисто мнимым периодом 2i. Действительно:

При изучении показательных функций нет смысла рассматривать их на всей комплексной плоскости.Достаточно ограничиться рассмотрением в любой полосе шириной 2. Обычно ограничиваются рассмотрением в полосе

, которая называется основной (рис. 1).

Р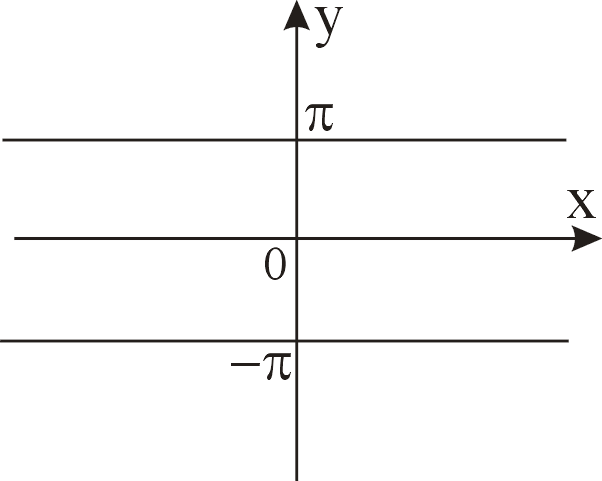ис. 1

3. Логарифмическая функция.

Число W называется логарифмом числа z и обозначается , если .

Пусть , а, тогда,

таким образом .

Аналогичным образом можно показать, что .

Таким образом ,,

,

Наряду с обозначением , используют, где- конкретное значение логарифма.

Пример.

Рис. 2

.

По формуле ,

4.Тригонометрические функции.

В соответствии с формулой Эйлера:

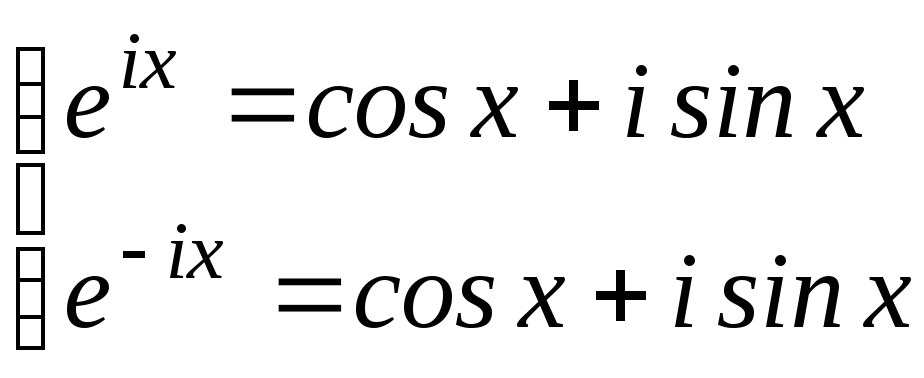(1)

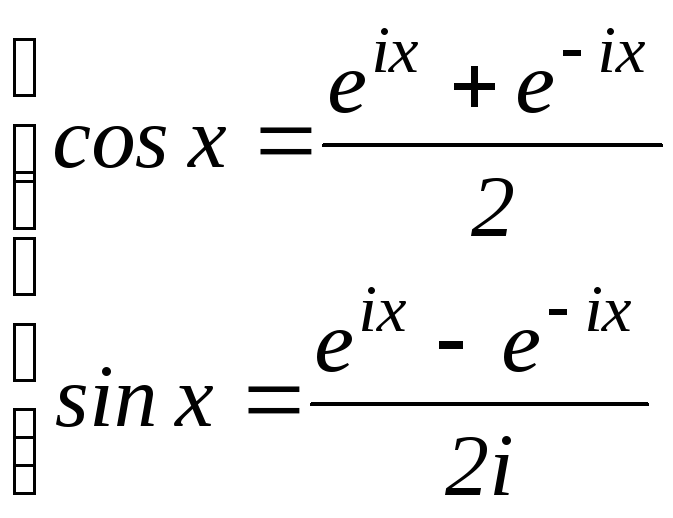(2)

Тригонометрические функции комплексного переменного по аналогии с (2) задаются как

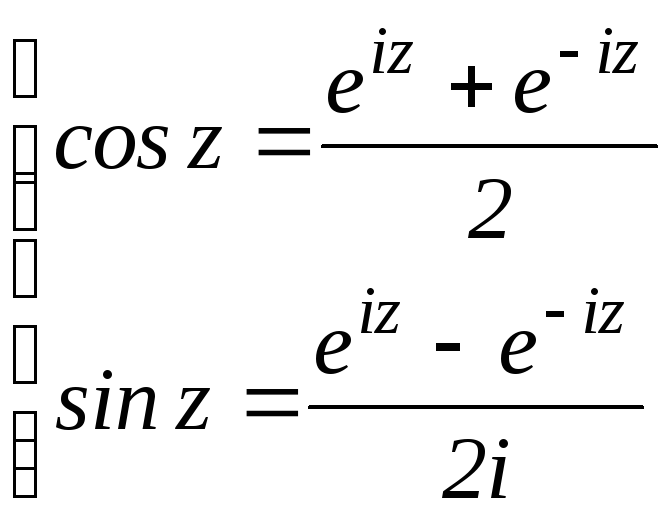(3)

Из сравнения (2) и (3) следует, что на множестве вещественных чисел соотношение (3) задает обычные тригонометрические функции.

Функции sin(z) и cos(z) – аналитические функции на всей комплексной плоскости, так как представляют собой линейную комбинацию показательных функций. При этом

. Аналогично .

sin(z) и сos(z) – тригонометрические функции периода 2, действительно:

.

Аналогично для sin(z).

Справедливы все известные тригонометрические тождества:

и т. д.

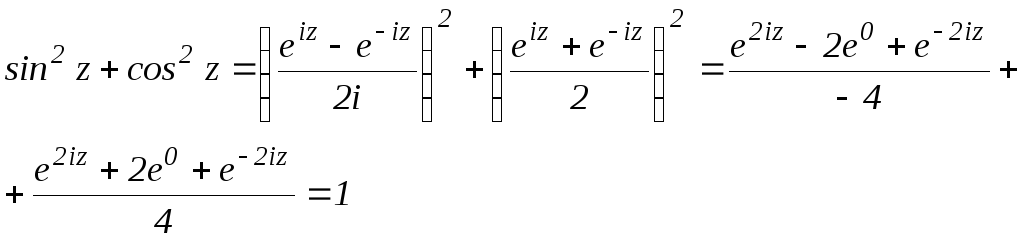
Определим, что в отличие от функции вещественного переменного функции cos(z) и sin(z) не ограничены по модулю.

5. Гиперболические функции.

Гиперболические функции по аналогии с функциями вещественного переменного определяются равенствами:

, .

Гиперболические функции являются аналитическими на всей комплексной плоскости.

6. Обратные тригонометрические функции.

По определению W=arccos(z), если cosW=z. Из этого следует, что

(1)

Умножим (1) на , имеем:(2)

Решая квадратное уравнение (2) найдем:

(корень алгебраический)

,

Аналогично можно показать, что .

ЛЕКЦИЯ 4

План лекции

1. Понятие контурного интеграла функции комплексного переменного.

2. Связь контурного интеграла с криволинейными интегралами функций вещественного переменного.

3. Свойства интегралов.

4. Теорема о независимости значения интеграла от пути интегрирования.

ПОНЯТИЕ КОНТУРНОГО ИНТЕГРАЛА ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО.

Пусть на некоторой плоскости z задан некоторый контур С, точками . Разобьем его наn (частей) дуг. На дуге произвольно выберем точку.

Р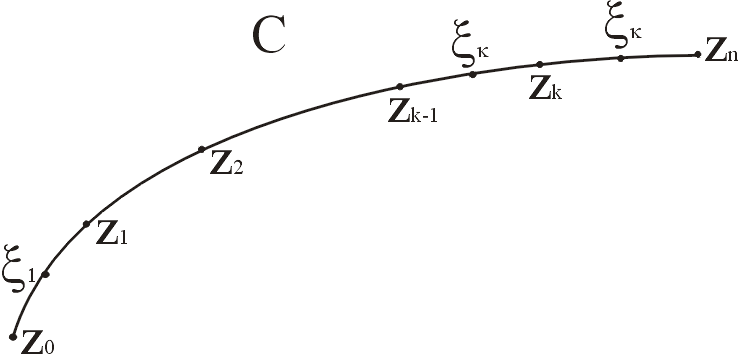ис. 1

Составим интегральную сумму: . Обозначим.