Свойства преобразований лапласа.

1.Линейность преобразований.

Теорема 1.

Если функция f₁(t) и f₂(t) являются оригиналами и имеют, соответственно, изображения F₁(s) и F₂(s), то преобразование Лапласа от соотношения

L[k₁ f₁(t) k₂ f₂(t)] = k₁F₁(s) k₂ F₂(s) ,

где k₁, k₂- некоторые константы.

Доказательство.

По определению преобразование Лапласа

L[k₁f₁(t)k₂ f₂(t)] =

k₁F₁(s) k₂ F₂(s).

Замечание.

Из данной теоремы следует, что преобразование Лапласа линейной комбинации оригиналов равно той же линейной комбинации их изображений.

L[] =- const.

2.Изображение производной.

Теорема 2.

Если функции f(t) и f'(t) функция f(t) имеет изображение F[s], то преобразование Лапласа производной этой функции равно:

L[f(t)] = s F[s] – f(0⁺)

f(0⁺) =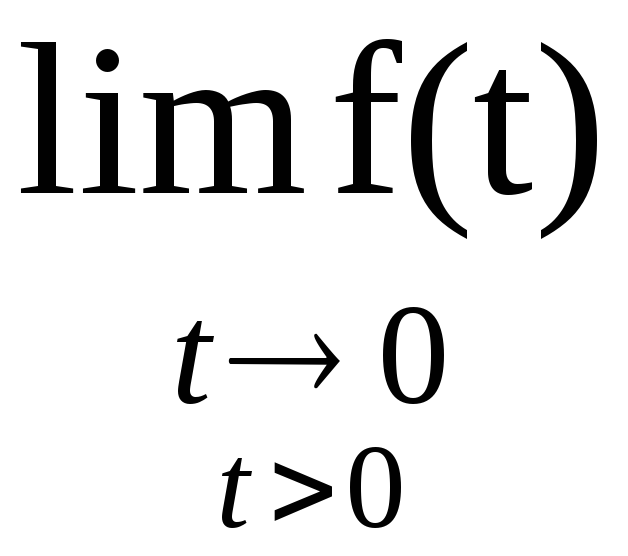

Теорема утверждает, что дифференцирование в вещественной области в комплексной области соответствует операции умножения изображения на s.

Доказательство.

По определению функция F[s] это:

F[s] =

] =

Покажем, что

при с > α.

Последовательное применение теоремы 2 позволяет распространить ее на производную любого порядка.

] =

Продолжая процесс, можно установить, что для n-ой производной:

3.Изображение интеграла.

Теорема 3.

Если функция f(t)-оригинал и имеет изображение F[s], то интеграл

также является оригиналом, причем

L[] = F(s)/s +

L[] = F(s)/s + /s.

Теорема утверждает, что интегрирование в вещественной области в комплексной области соответствует делению изображения на s (с точностью до const).

Доказательство. (2-ой части, которая приводит к формуле задания изображения).

По определению

F(s) =

L[

Покажем, что

при .

Теорема доказана.

4.Изменение масштаба.

Теорема 4.

Если функция f(t) оригинал и имеет изображение F(s), и «a» - некоторая положительная константа или положительная переменная независящая от t и s, то преобразование Лапласа:

L =

График функции отличается от графика функцииf(t) наличием масштаба по оси t.

Доказательство.

По определению

F(W) =

Положим, имеем

Введем , тогда

L = .

Пример.

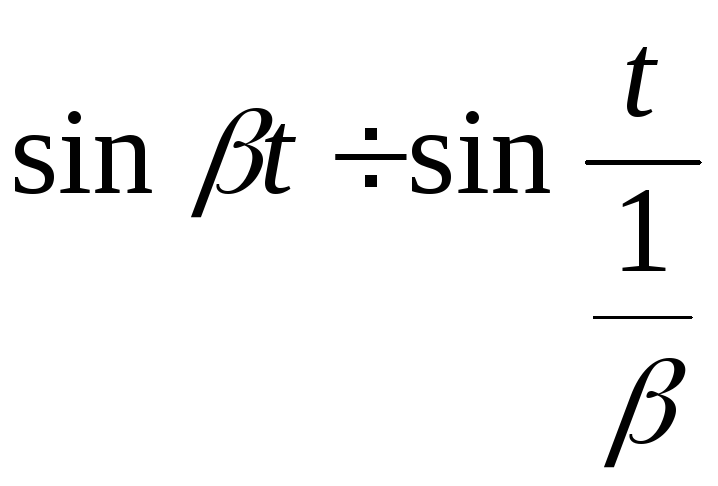
В соответствии с теоремой 4.

.

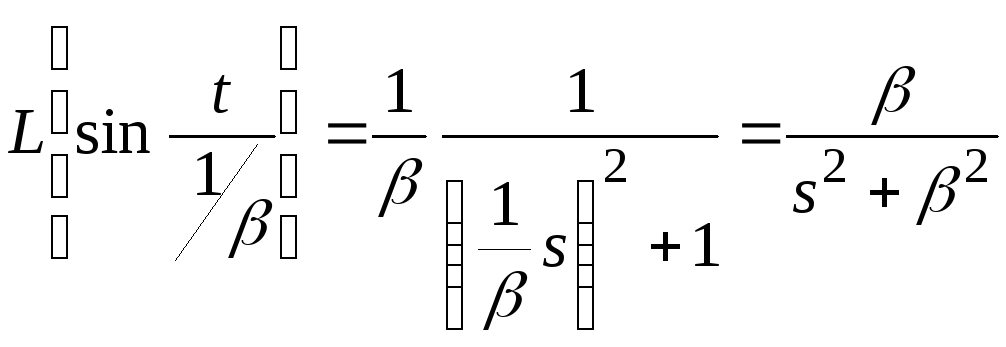5.Смещение в комплексной области.

Теорема 5.

Если функция f(t) оригинал и имеет изображение F(s), то

Доказательство.

По определению преобразование Лапласа

.

Пример 1.

Найти преобразование Лапласа.

по теореме 5

Пример 2.

Найти обратное преобразование Лапласа.

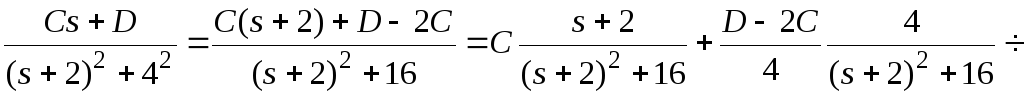
6. Теорема свертки.

Сверткой функции f₁(t) и f₂(t) называется функция

f(t) =

Операция свертки обладает коммутативностью, т. е.

=

Действительно,

=

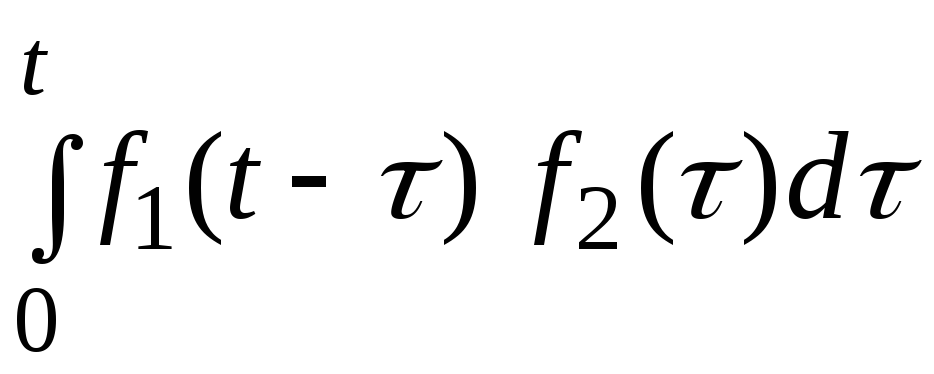Лекция 13

План лекции

1. Свертка функций. Теорема об изображении свертки функций.

2. Изображение запаздывающей функции.

3. Изображение -функции и ее производных.

4. Дифференцирование в комплексной области.

Теорема 6.

Если функции f₁(t) и f₂(t) являются оригиналами и имеют соответственно изображения F₁(s) и F₂(s), то

L[] = F₁(s)∙ F₂(s)

Теорема утверждает, что произведению изображений в вещественной области соответствует интеграл свертки.

Доказательство.

Обозначим F(s) = L[]

По определению

F(s) =

Верхний предел во внутреннем интеграле можно перенести из т. t в т. ∞, если подынтегральное выражение умножить на 1().

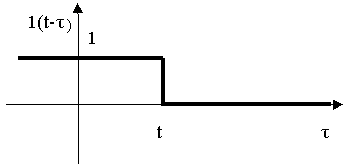
Рис. 1.

F(s) =

Изменим порядок интегрирования

F(s) =

Принимая во внимание вид функции 1(t-τ) как функции аргумента t, запишем

F(s) =

Для второго интеграла введем подстановку Отсюда следует, что

;

F(s) =

=

Рис. 2.

Замечание.

Может показаться на первый взгляд, что теорему свертки удобно использовать для вычисления обратного преобразования Лапласа. На самом деле это не так, интеграл свертки приводит к громоздким вычислениям.

7.Изображение запаздывающей функции.

Теорема 7.

Если функция f(t) является оригиналом и имеет изображение F(s), то преобразование Лапласа запаздывающей функции:

при условии

при t < τ . (*)

Доказательство.

По определению

F(s) =

Положим , тогда

F(s) =

Принимая во внимание соотношение приt < τ нижний предел можно перенести из т. τ в т.0. Получим

F(s) = отсюда следует, что

.

Замечание 1.

По условию теоремы функция f(t) является оригиналом, следовательно, может быть записана в виде: f(t)·1(t). Запаздывающий оригинал имеет вид:

, т. е. запаздывающий оригинал обязательно удовлетворяет условию (*).

Замечание 2.

При пользовании данной теоремой во избежание ошибок оригинал следует записывать в виде f(t)·1(t).

Пример 1.

Н

f(t)

айтиL[]

t

4

По теореме 7 найдем функцию f(t)·1(t)

f(t-4)·1(t-4) = t² 1(t-4) . Очевидно

f(t)·1(t) = (t + 4)² 1(t)

по теореме запаздывания

L[] =

Пример 2.

Н

айти

t

5

по теореме запаздывания

= (t – 5) 1(t – 5).

8.Предельный переход по второй независимой переменной.

Теорема 8.

Пусть а – переменная независящая от t и s. Если функция f(t,а) является оригиналом относительно переменной t и имеет изображение F(s,a), то при условии существования выписанных ниже пределов справедливо равенство:

Доказательство.

По определению

Перейдем к пределу

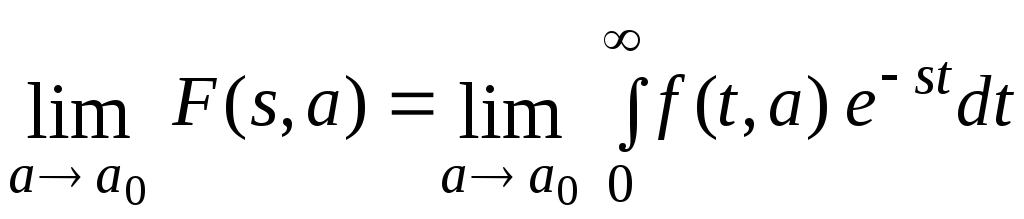
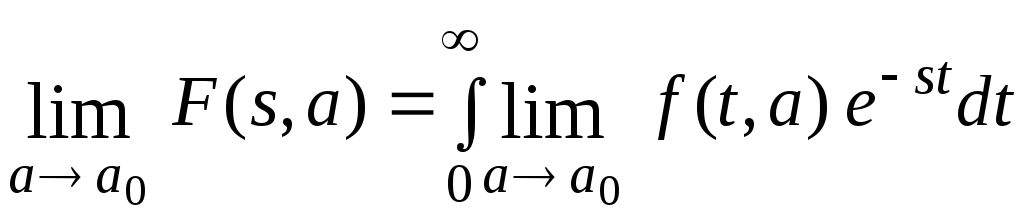
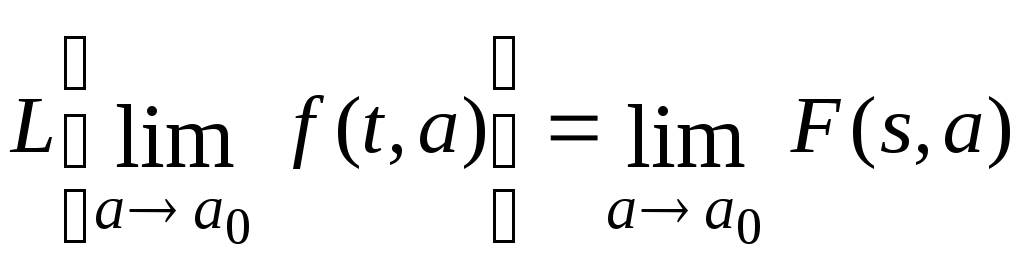
Используя эту теорему, найдем изображение δ - функции. Рассмотрим функцию f(t,a), изображенную на рисунке.

f(t,a)

1/a

t

a

Очевидно,

f(t,a) =

L[f(t,a)] =

L[f(t- τ)] = где

Рассмотрим предел

т.о.

В соответствии с теоремой 8:

L[δ(t)] =

Т. о. Получили L[δ(t)] = 1.

Для производной δ(t) справедливо соотношение

Это равенство формально может быть получено применением теоремы 2.

Для запаздывающей δ(t) справедливо соотношение

L[δ(t-τ)] =

L[ (в соответствии с теоремой 7).

9.Дифференцирование в комплексной области.

Теорема 9.

Если функция f(t) является оригиналом и имеет изображение F(s), то

L

Теорема утверждает, что дифференцирование изображений в вещественной области соответствует умножению оригинала на аргумент t.

Доказательство.

По определению

F(s) =

Продифференцируем равенство по s. Это возможно, т. к. F(s)- аналитическая функция в области Re s > .

F(s) =

Перейдем к дифференцированию под знаком интеграла, получим

F(s) = L

В соответствии с таблицей

По теореме 9

L[

L[

Аналогично

L[