начерт

82

2. k = Ô - построение линии k пересечения конической поверхности и плоскости подробно разобрано в примере 9.1.

3. K,N = ka: K1 =k1a1 ; K2a2; N1=k1a1; N2a2.

Точка K видна относительно Ï1, а точка N не видна (см. пример 9.1 и рис. 9.4). Поэтому прямая a видна относительно Ï1 левее точки K и не видна между точками K и N и на небольшом участке правее точки N. Граница видимости точек конической поверхности относительно Ï2 - контурные образующие t1и t2. Точки, лежащие на них и перед ними, относительно Ï2 видны, а остальные не видны. Следовательно, относительно Ï2 прямая видна правее точки N и не видна между точками K и N и на участке левее точки K.

Рис. 9.6

83

Отрезок прямой a между точками M и N находится внутри сферы и не виден. Видимость прямой a на других участках зависит от видимости точек M и N относительно той или иной ПП (относительно Ï1 M видна, N не видна, а относительно Ï2 видны и M, и N).

На рис. 9.7 при нахождении точек M и N пересечения горизонтали h с конической поверхностью вращения h заключали в плоскость Ï1, пересекающую поверхность по окружности m.

1.l, Ï1 l1 1.

2.g = Ô (g11, а g2- треугольник 122232, где 1, 2, 3 - точки пересечения плоскости с ребрами поверхности Ô).

3.M,N = g l.

Видимость прямой l на участках левее точки M и правее точки N определяется видимостью M и N относительно той или иной ПП, а между точками M и N прямая не видна.

цилиндрические поверхности и т. д. В общем случае поверхности 2-го порядка пересекаются между собой по пространственной кривой 4-го порядка.

Теорема Монжа: если две поверхности 2-го порядка описаны около третьей поверхности 2-го порядка или вписаны в неё, то линия их пересечения распадается на две кривые 2-го порядка, плоскости которых проходят через прямые, соединяющие точки пересечения линий касания.

На рис. 9.11 пересекаются коническая и цилиндрическая поверхности, описанные вокруг сферы. Сфера касается конической поверхности по окружности q, а цилиндрической поверхности - по окружности m. Окружности q и m пересекаются в точках A и B, определяющих прямую d. Поверхности пересекаются по двум эллипсам e1 и e2, плоскости которых проходят через прямую d.

86

Л Е К Ц И Я 10

ГЕОМЕТРИЧЕСКИЕ ТЕЛА 10.1. Общие замечания

Геометрическим телом называют замкнутую часть пространства, ограниченного отсеками поверхностей.

Геометрические тела делят на простейшие - тела, образованные одной поверхностью (шар, тор и т. д.) или ограниченные отсеком исходной поверхности и поверхностями (обычно плоскостями), образующими границы отсека исходной поверхности (цилиндр, конус, призма, пирамида т. д.), и сложные - тела, состоящие из нескольких простейших тел (рис. 10.7).

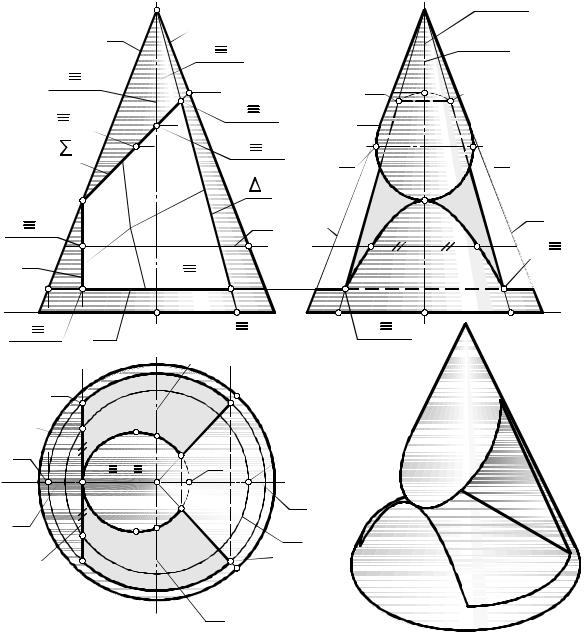
На рис. 10.1 дан КЧ простейших геометрических тел: шара - части пространства, ограниченного сферой; цилиндра вращения - части пространства, ограниченного отсеком цилиндрической поверхности вращения и двумя плоскостями уровня и ; конуса вращения - части пространства, ограниченного конической поверхностью вращения, плоскостью уровня Ã и вершиной T.

2T2

x

T1

Рис. 10.1 10.2. Построение изображений геометрических тел с вырезами

Особо важно для дальнейшего обучения научиться строить изображения простейших геометрических тел с вырезами на горизонтальную Ï1, фронтальную Ï2 и профильную Ï3 ПП (в разделе 10.2 Ï3 - профильная ПП). Для установления проекционной связи изображений на Ï1 и Ï3 тело связывают с системой координат Oxyz и проецируют её оси вместе с телом. Координатные плоскости Oxz, Oxy и Oyz задают параллельно плоскостям проекций и по возможности совпадающими с плоскостями симметрии тела, с его гранями, основанием и т. д. В этом случае проекционное соответствие между полями проекций Ï1 и Ï3 (см. рис. 10.3 - 10.6) устанавливает общая для этих полей координата Y.

87

ПРИМЕР 10.1. Заданы изображения пирамиды на Ï1 (вид сверху) и Ï2 (вид спереди) и основные проекции фронтально проецирующих плоскостей, образующих сквозной

сводится к построению горизонтальных и профильных проекций указанных линий пересечения по их известным фронтальным проекциям и условию их принадлежности пирамиде.

Ось z пространственной системы координат, устанавливающей проекционную связь изображений пирамиды на Ï1 и Ï3, совместили с высотой, проведенной из вершины T пирамиды на плоскость , начало системы отсчета точку O взяли в точке пересечения этой высоты с , а координатные плоскости Oxz и Oyz расположили параллельно Ï2 и Ï3 соответственно.

Для построения изображения пирамиды на Ï3 на свободном месте чертежа правее z2 провели z3 z2, с помощью линии связи

y3 отложили координату YA и получили точку A3, а затем от точки O3 по оси y3 вправо отложили координату YB и получили точку B3. YA и

T3 A3T3D3 .

Секущие плоскости Ã и пересекаются с пирамидальной поверхностью по ломаной [1, 2, 4, 6, 7, 5, 1], а между собой - по отрезку [4, 5].

90

обозначены k2 на рис. 10.4. Решение задачи сводится к построению горизонтальных и профильных проекций указанных линий пересечения по их фронтальным проекциям.

Виды конуса на Ï1 (окружность) и Ï3 (треугольник) располагают в проекционной связи с видом конуса на Ï2 . Положение проекций осей и начала отсчета системы координат, связанной с конусом, указаны на рисунке.

Плоскость пересекает поверхность конуса по эллипсу, который на Ï2 проецируется в отрезок [A2,L2], а на Ï1 и Ï3 в эллипсы. Для их построения использовали характерные точки A, G, N, B, L, C, S, Q и не обозначенные промежуточные точки, взятые между характерными точками. Точки A и L расположены на контурных относи-

жайшей и дальней точками эллипса, а на Ï3 - его самой правой и левой точками соответственно. B и C - общие точки эллипса и прямолинейных образующих, по которым плоскость пересекает коническую поверхность. Дуга эллипса BLC не существует, но строится и обводится тонкой линией.

Плоскость Ã пересекает коническую поверхность по дуге гиперболы KAF (точка A - её вершина, точки K и F - общие точки гиперболы и дуг окружности, по которым поверхность конуса пересекает плоскость Ô). Гипербола на Ï1 и Ï2 проецируется в отрезки прямых, а на Ï3 в натуральную величину, для построения которой кроме точек A, K и F используются промежуточные точки, фронтальные проекции которых расположены между A2 и K2 F2.

Уже отмечалось, что коническая поверхность пересекается плоскостью , проходящей через вершину T конуса, по отрезкам образующих ([B,D] и [C,E]), а плоскостью Ô, перпендикулярной оси j конуса, - по дугам окружностей (F,D и K,E), которые на Ï2 и Ï3 прое-