
начерт
.pdf
|
|
|
|
|
|
|
41 |
|
|
|
|
|
|
|
|
|
ПРИМЕР 5.1. Заданы точка M и плоскость |
(A,a) (рис. 5.4). |
|
||||||||||||
M, - найти расстояние от точки M до плоскости |
без преобразо- |
||||||||||||||
вания КЧ. |
|
|
|
|
|
l |
M l |
|
- из точки M строится |
||||||
|
Пояснения к решению: |
1. |
|
||||||||||||
перпендикуляр |
l |
к плоскости |
, для чего в |
задаются горизонталь |
|||||||||||
h (h1,h2) и фронталь f (f1,f2), а затем проводят |
l1 |
|
h1 |
l2 f2 . |
|||||||||||
2. |
K=l |
- ищется точка K |
пересечения l |
и |
(l |
заключалась в |
|||||||||
плоскость Ã Ï2 , |
строилась прямая t=Ã |
, а |
затем |
точка |
K=t |
l). |
|||||||||
3. |
M,K - |
определяется длина отрезка |
M,K |
(по правилу прямо- |
|||||||||||
угольного треугольника), равная искомому расстоянию |
M, . |
|
|||||||||||||
|
A2 |
12 |
|
h2 |
M2 |
|
t2 Ã2 l2 |
|
|
|
|
|
|
||
|
|
32 |
|
|
|
|
|
|
|
||||||
|
a2 |
2 |
f |
K2 |
|
B |
|
|
|
M2 |
|
K2 |
h2 |
|
|
|
2 |
2 |
42 |
|
|
|
|
|
|
|
|
|
|
|
|
|
a1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
21 |
f1 |
|
M1 |
|
|
|
M1 |
|
|
|
1 |
|
|
|
A1 |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
41 |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
M,K |
|
|
|
h1 |
|
|||
|
h1 |
|
|
|
|
|
|
|
|
|
K1 |
|
|||
|
11 |
|
K |
|
|
M,K |
|
|
|
|
|
||||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l1 |
|
D |
|
|
|
|
Рис. 5.5 |
|
|
||
|
|
|
|
31 |
|
|
|
|
|
|
|
|
|
||
|
|
Рис. 5.4 |
|
|
|
|
|
|
|
|
|
|
|||
|
ПРИМЕР 5.2. Заданы точка M и плоскость |
Ï1 (рис. 5.5). |
|
||||||||||||
M, |
- найти расстояние от точки M до плоскости . |
|
|
|
|
||||||||||
|
Пояснения к решению: |
1. |
h |
M |
h |
- так как |
Ï1 , |
то |
|||||||
перпендикуляр к является горизонталью h (h1 |
|
1). |
2. |
K=h |
|
||||||||||
- поскольку |
|
Ï1, то |
K1 =h1 |
|
1 , а |
K2 |
h2 . |
3. |
M, |
= M,K |
- |
||||
[M,K] h
h 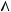 h
h 
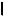 Ï1
Ï1 
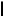 M,K
M,K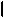 =
=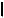 M1,K1
M1,K1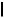 .
.
Таким образом, если плоскость проецирующая, то отрезок перпендикуляра, определяющий расстояние от точки до плоскости, строится сразу, так как он параллелен одной из ПП. Поэтому при нахождении расстояния от точки до плоскости общего положения часто применяют преобразование чертежа, решая 3ОЗПЧ и переводя плоскость в проецирующее положение (пример 5.3).
42
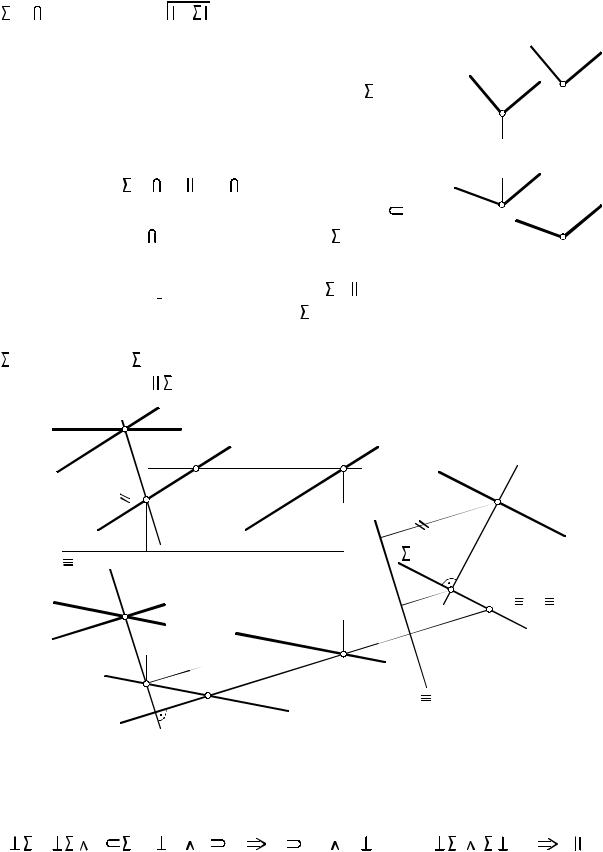
ПРИМЕР 5.3. Заданы точка M и плоскость 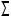 (a
(a  b) (рис. 5.6).
b) (рис. 5.6). 
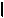 M,
M,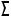
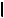 - используя способ введения новой ПП, найти расстояние от
- используя способ введения новой ПП, найти расстояние от
точки M до плоскости 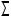 .
.
Прямая t на рис. 5.6 отношения к примеру 5.3 не имеет.
В основе решения примера 5.3 лежат 3ОЗПЧ и пример 5.2 (рис. 5.5).
Пояснения к решению: 1.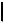 Ï3
Ï3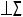
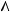 Ï3
Ï3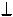 Ï1 - задав новую ПП Ï3
Ï1 - задав новую ПП Ï3
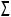 ,
,
плоскость |
делают проецирующей и строят её проекцию 3. |
Для |
|||||||||||||
этого задают h |
|
и оси проекций x1 2 |
(M1 ,M2) и x1 |
3 |
h1 , а затем, |
||||||||||
найдя проекции 13 |
и 33 точек 1 и 3 плоскости, проводят через 13 и 33 |
||||||||||||||
её проекцию |
|
3. |
2. |
l |
M l |
- строят проекции l1 и l3 |
перпен- |
||||||||
дикуляра l к плоскости |
, проходящего через точку M: |
а) |
l |
h |
|||||||||||
|
l h |
|
l1 M1 l1 h1; б) |
Ï3 l |
|
l Ï3 |
l3 |
M3 l3 |
3. |
||||||
3. K=l |
- строят проекции точки пересечения l и |
: K |
|
l |
K |
|
|||||||||
Ï3 |
K3 =l3 |
|
3 |
K1 |
l1 . Для получения K2 из K1 проводят линию |
||||||||||
связи (K1 ,K2) |
|
x1 |
2 |
и откладывают от x1 |
2 |
по линии связи расстоя- |
|||||||||
ние, равное расстоянию от точки K3 |
до оси x1 3. Через K2 и M2 про- |
||||||||||||||
ходит |
l2 . |
|
4. |
M, |
= M,K - |
искомое |
расстояние равно длине |
||||||||
|
l |
|
|
|
отрезка |
M,K : [M,K] |
l l |
Ï3 |
|
M,K = M3,K3 . |
|||||
|
2 |
|
M2 |
|
|
|
|
|
|
|
|
|
|
|
|
t2 |
|
|
|
12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b2 |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
22 |
|
|
K2 |
h2 |
|
|
|
l3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
a2 |
|
|
|
|
|
32 |
|
|
|
M3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
x1 2 |
l1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t1 |
|
|
|
|
|
h3 |
33 |
|
M,K |
|
|
|
|
|
|
M1 |
|
|
|
31 |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
a1 |
|
|
|
|
|
|
K3 |
|
3 |
|
|
|
|
|
|
h1 |
21 |
|
|
|
|
|
|
|
|
|
13 |
|
|
|
|
|
|
K1 |
b1 |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
x1 |
3 |
|
|
|
|
|
|
|
11 |
Рис. 5.6 |
|
|
|
|
|
|
|
43 |
|
|
|
|
|
|
|
|
|
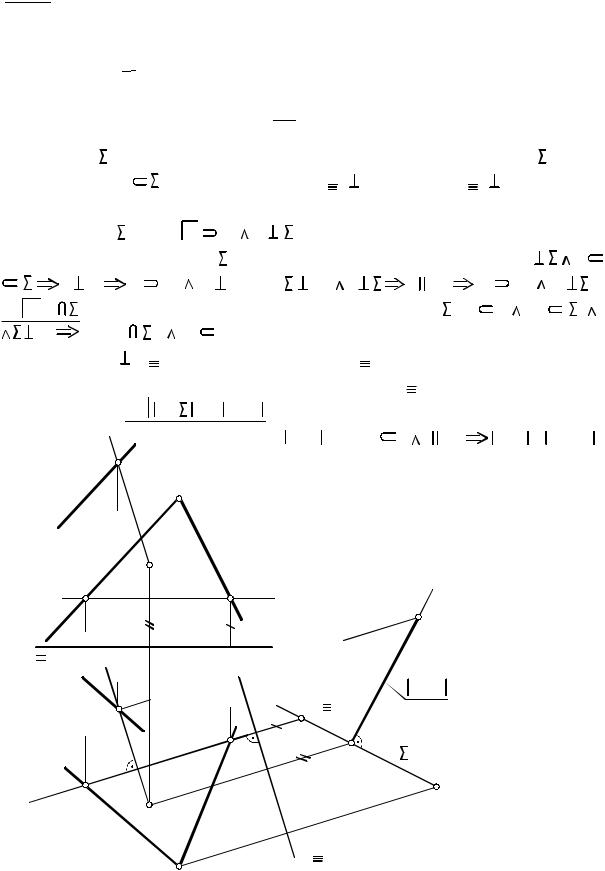
ПРИМЕР 5.4. |
Заданы параллельные прямая t и плоскость |
|||||||||||||||
(a b) (рис. 5.6). |
t, - найти расстояние от прямой до плоскости. |
|||||||||||||||
Для выполнения примера 5.4 |
достаточно |
d2 |
|
|
|
a2 |
b2 |
|||||||||
на прямой |
t |
взять произвольную точку M и |
|
|
|
|
|
|||||||||
найти расстояние от неё до плоскости |
с ис- |
|
|
|
|
g2 |
|
|||||||||
пользованием новой ПП, как в примере 5.3, или |
M2 |
|
|
|
|
|||||||||||
без преобразования КЧ, как в примере 5.1. |
|
|
|
|
|
g1 |
|
|||||||||
Для |
|
определения |
расстояния |
между |
d1 |
|
|
|
|
|||||||
плоскостями |
(a |
b) |
Ã(d |
g) (рис. 5.7) достаточ- |
|
|
|
|
b1 |
|||||||
но найти расстояние от какой-то точки M |
Ã, |
M1 |
|
|
a1 |
|||||||||||
|
|
|
||||||||||||||
например M = d |
g, |
до плоскости |
|
так, |
как |
|
|
|
|
|
|
|||||
это сделано в примерах 5.1 или 5.3. |
|
|
|
|
Рис. 5.7 |
|||||||||||
ПРИМЕР 5.5. Задана плоскость |
(a b) (рис. 5.8). Построить плос- |
|||||||||||||||
кость Ã, параллельную плоскости |
и удаленную от неё на 20 мм. |
|||||||||||||||
Для выполнения примера надо через какую-то точку плоскости |
||||||||||||||||
провести к |
|
отрезок перпендикуляра длиной 20 мм, а затем за- |
||||||||||||||
дать плоскость Ã |
, проходящую через конец отрезка. |
|
|
|
|
|
||||||||||
e2 |
K2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12 |
h |
2 |
2 |
|
|
|
|
|
|
|
|
t2 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
l3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
M2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
a2 |
|
|
|
|
b2 |
|
|
|
|
|
K |
3 |
|
à |
||
|
|
|
|
l2 |
|
|
|
|
|
|
|
|
|
|
3 |
|
x1 2 |
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
l |
1 |
|
|
|
|
|
|
|
M3 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
t1 |
|
|
|
|
|
|
|
|
|
|
1 |
3 |
2 |
h |
||
|
|
|
|
|
|
|
|
|
|
|
|
3 |
3 |
|||
|
K1 |
|
|
|
b1 |
|
|
|
|
|
|
|
|
|
||
e1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
h1 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
M1 |
|
|
|
|
1 |
|
x1 |
|
|
|
|
|
|
|
|
|
|
11 |
|
a1 |
|
|
3 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 5.8
Пояснения к решению: 1. Плоскость 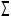 делают проецирующей, задав Ï3
делают проецирующей, задав Ï3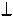 h, где h - произвольная горизонталь плоскости, и строят её проекцию
h, где h - произвольная горизонталь плоскости, и строят её проекцию 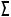 3, используя точки 1,M
3, используя точки 1,M
 . 2. Через точку M проводят
. 2. Через точку M проводят
l : l |
h ; l h l M l1 M1 l1 h1 и l |
Ï3 l Ï3 |
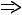 l3
l3  M 3
M 3  l3
l3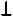
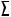 3. 3.Так как l
3. 3.Так как l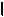
 Ï3, то от M3 по l3 отложили отрезок
Ï3, то от M3 по l3 отложили отрезок
44
длиной 20 мм и получили точку K3, а затем на l1 - точку K1 . Точку K2
нашли на линии связи, проведенной из |
K1 перпендикулярно оси |
|||
x1 2 , с использованием расстояния |
от |
точки K3 |
до |
оси x1 3 . |
4. Ã K Ã - в поле Ï3 провели Ã3 |
3, а в полях Ï1 и Ï2 плоскость |
|||
à задали пересекающимися прямыми t и e ( t a |
e |
h). |
||
5.3. Определение расстояния от точки до прямой линии
Расстояние от точки до прямой линии равно длине отрезка перпендикуляра, опущенного из этой точки на прямую.
Расстояние между параллельными прямыми равно длине отрезка перпендикуляра, опущенного из произвольной точки одной прямой на другую прямую. Поэтому для определения расстояния между параллельными прямыми достаточно на одной из них взять какую-то точку и решить ключевую задачу - найти расстояние от этой точки до второй прямой.
ПРИМЕР 5.6. Заданы точка M и прямая a Ï1 (рис. 5.9).
Ï1 (рис. 5.9). 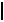
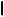 M,a
M,a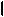 - найти расстояние от точки до прямой.
- найти расстояние от точки до прямой.
a2 |
|
h |
l2 |
K |
|
|
|
l2 |
K |
h |
|
|
|
|
|
2 |
|
|
|
|
2 |
|
|
|
|||||
|
|
2 |
|
|
|
|
2 |
|
|
|
|
|||
h2 |
M2 |
|
|
|
M2 |
|
x1 |
2 |
M2 |
|
|
|
|
|
K2 |
|
|
|
|
|
|
|
|
|
|||||
h1 |
|
M,K |
|
M1 |
|
|
M1 |
|
|
|
|
|||
M,K |
|
|
h1 |
|
M3 |
|
|
|||||||
|
|
|
|
l1 |
|
|
|
|
|
|
||||
|
M1 |
|
D |
|
|
|
|
|
|
|
|
|
||
|
|
|
h1 |
|
|
l1 |
|
|
|
|
M,K |
|||
K1 a1 |
|
|
K |
|
|
K |
|
|
|
|||||
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x1 3 |
K |
3 |
h |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
Рис. 5.9 |
|
|
Рис. 5.10 |
|
|
|
Рис. 5.11 |
|
|
|
||||
Пояснения к решению: 1. |
h |
M |
h |
a - так как |
a |
|
Ï1, то пер- |
|||||||
пендикуляр к a |
параллелен |
Ï1 . |
2. |
K=h |
a - |
K1 |
a1 K2=h2 |
|
a2. |
|||||
3. M,a = M,K = M1,K1 |
- поскольку [M,K] h h |
Ï1, то отрезок [M,K] |
||||||||||||
проецируется на |
Ï1 в натуральную величину. |
проецирующей, |
то |
|||||||||||
Таким |
образом, |
если |
прямая |
является |
||||||||||
перпендикуляр к ней параллелен одной из ПП и расстояние от точки до прямой ищется с использованием простейших свойств прямых частного положения.

|
|
|
45 |
|
|
|
|
|
|
|
|
ПРИМЕР 5.7. Заданы точка M и прямая h |
Ï1. |
M,h |
- найти |
||||||||
расстояние от точки M до прямой h |
без преобразования КЧ (рис. |
||||||||||
5.10) и с преобразованием КЧ (рис. 5.11). |
|
l |
M |
l |
h |
l |
h - |
||||
Пояснения к решению на рис. 5.10: |
1. |
||||||||||
так как l h h |
Ï1, то строят l1 |
M1 |
l1 |
h1 , ищут K1 = l1 |
h1 |
K2 |
h2 |
||||
и проводят l2 |
M2,K2. |
2. M,h = |
M,K |
- длина отрезка |
M,K |
прямой |
|||||
общего положения l |
найдена по правилу прямоугольного треуголь- |
||||||||||
ника ( M1K1D), построенного в поле Ï1. |
1. |
l |
M |
l |
h |
l |
h - |
||||
Пояснения к решению на рис. 5.11: |
|||||||||||
см. пояснения к рис. 5.10. 2. Чтобы отрезок [M,K] прямой общего положения проецировался на ПП в натуральную величину, надо чтобы эта ПП была параллельна отрезку и, следовательно, перпен-
дикулярна h: |
Ï3 |
h |
Ï3 Ï1 - проводят |
x1 2 |
(M1,M2) и |
x1 3 |
h1, |
строят M3 и |
K3 |
h3 |
и получают M3,K3 |
= M,K . |
|
|
|
ПРИМЕР 5.8. Заданы прямая a и точка |
M (рис. |
5.12). |
Без |
||||
преобразования КЧ найти расстояние от точки M до прямой a. |
|
||||||
Прямая b на рис. 5.12 отношения к примеру 5.8 не имеет. Пример выполнялся согласно такому ПА (первые два пункта
ПА нужны для получения отрезка, определяющего искомое расстояние):
1. |
M |
|
a (1ОМЗ) - горизонталью h |
M |
h |
a (h1 |
a1) и |
|||||
|
1 |
|
f |
|
|
|
фронталью f |
M |
f |
a |
(f2 a2 ) |
была |
|
2 |
2 |
|
|
|
задана плоскость |
, |
содержащая мно- |
||||
M,K |
|
|
|
|
|
|||||||
E |
|
|
|
K2 |
|
|
жество всех прямых, проходящих через |
|||||
h2 |
|
|
|
|
|
|
точку M перпендикулярно прямой a. |
|||||
|
|
|
|
22 |
|
2. K= |
a (1ГПЗ) - для нахожде- |
|||||
M2 |
|
b2 |
|
|
|
|||||||
|
|
|
|
ния точки K использованы построе- |
||||||||
|
|
|
|
|
|
|||||||
|
|
a |
2 |
à |
t |
|
ния: 1. à a à Ï2; 2. t=à |
; 3. K=t a. |
||||
|
|
|
2 |
2 |
|
Через точку K пересечения прямой a |
||||||
x1 2 |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
с плоскостью |
проходит определяю- |
|||||
h |
|
11 |
|
F |
|
f1 |
щий искомое расстояние отрезок [M,K] |
|||||
|
|
|
перпендикуляра, опущенного из точки |
|||||||||
|
|
|
|
|||||||||
b |
M1 |
|
|
K |
t |
M на прямую a. |
|
|
|
|
||
|
|
|
3. M,a = M,K (2ОМЗ) - длина отрез- |
|||||||||
|
|
|
|
|
1 |
1 |
||||||
|
|
a1 |
|
|
21 |
|
ка M,K = E,K2 |
найдена из треугольника |
||||
|
Рис. 5.12 |
|
|
K2 M2E, в котором |
E,M2 = K1,F . |
|
||||||
|
|
|
|
|
|
|
|
|
|
|||

|
|
|
|
46 |
|
|
|
|
|
|
ПРИМЕР 5.9. |
Заданы точка M и прямая a (рис. 5.13). |
M,a - |
||||||
используя способ введения новой ПП, найти расстояние от точки M |
|||||||||
до прямой a. |
|
|
|
|
|
|
|
|
|
|
Прямая b на рис. 5.13 отношения к примеру 5.9 не имеет. |
|
|||||||
|
|
22 |
a2 |
Цель введения новой ПП в |
|||||
|
K |
примере |
- сделать |
прямую a |
|||||
|
2 |
|
|
общего |
положения |
проецирую- |
|||
|
12 |
|
b2 |
||||||
|
M |
щей, чтобы несущий искомое |
|||||||
|
|
|
2 |
расстояние отрезок |
[M,K] перпен- |
||||
x1 |
|
|
|
||||||
2 |
|
M1 |
дикуляра, опущенного из точки M |
||||||
x1 |
11 |
|
на прямую a, проецировался на |
||||||
3 |
|
b1 |
ПП в натуральную величину. Для |
||||||
1 |
K1 |
|
этого на прямой |
a |
взяли произ- |
||||
|
|
вольные точки 1 |
и 2 и последова- |
||||||
3 |
21 |
|
|||||||
|
a3 |
|
тельно задали две новые ПП: |
||||||
|
|
a1 |
1. Ï3 a |
Ï3 Ï1 |
- прямая a стала |
||||
|
M3 |
|
|||||||
|
|
|
прямой уровня. |
|
|
|
|
||
|
K3 |
x3 4 |
2. Ï4 a |
Ï4 Ï3 - прямая a стала |
|||||
|
23 |
||||||||
|
|
|
проецирующей. |
|
|
|
Ï4 |
||
|
K4 a4 14 |
|
|
В итоге получили: a |
|||||
|
|
M4 |
[M,K] a [M,K] Ï4 |
|
M,K = M,a = |
||||
|
|
M,K |
|
= M4,K4 |
. Точка K3 найдена из |
||||
|
Рис. 5.13 |
|
условия |
[M3 ,K3 ] |
a3 |
(теорема о |
|||
|
|
проецировании прямого угла). |
|||||||
ПРИМЕР 5.10. Заданы прямые a 
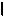 b (рис. 5.12 и 5.13). Найти расстояние между этими прямыми.
b (рис. 5.12 и 5.13). Найти расстояние между этими прямыми.
Для определения расстояния между параллельными прямыми a и b на прямой b берут произвольную точку M и находят расстояние от неё до прямой a без преобразования КЧ (см. пример 5.8 и рис. 5.12) или с использованием новой ПП (см. пример 5.9 и рис. 5.13).
5.4. Расстояние между скрещивающимися прямыми
Расстояние между скрещивающимися прямыми определяется длиной отрезка общего перпендикуляра, проведенного к обеим прямым. В учебном курсе это расстояние определяется с использованием способа введения новой ПП.
|
|
|
|
|
47 |
|
|
|
|
|
|
|
|
|
|
|
|
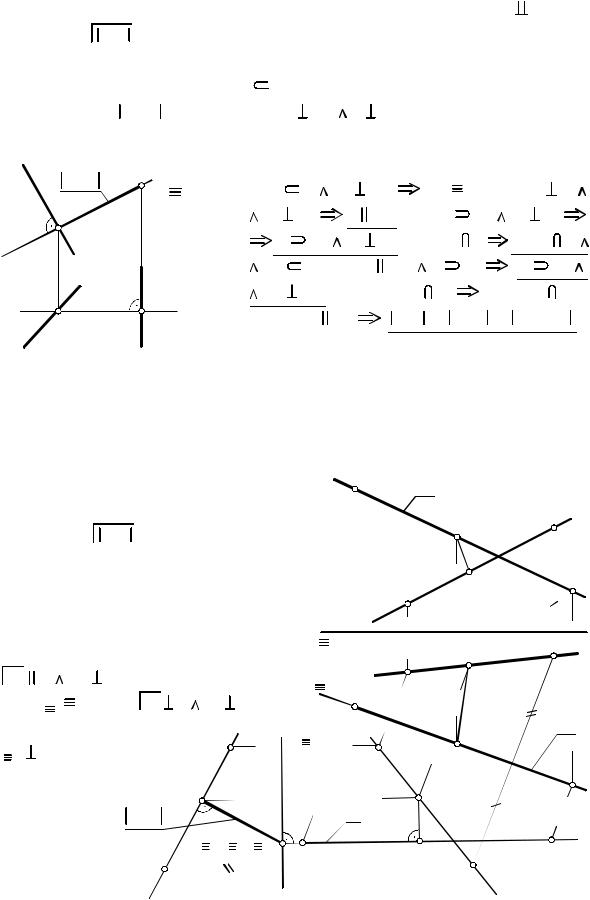
ПРИМЕР 5.11. |
Заданы скрещивающиеся прямые |
a |
Ï2 |
и b |
|||||||||||
(рис. 5.14). a,b - найти расстояние между этими прямыми. |
|
|
||||||||||||||
|
Пусть l - |
перпендикуляр к прямым a |
и b, пересекающий |
a в |
||||||||||||
точке M и b в точке K ([M,K] |
l). Тогда искомое расстояние равно |
|||||||||||||||
длине отрезка |
M,K . Поскольку a |
Ï2 |
l |
a, то перпендикуляр l к |
||||||||||||
прямой a и, следовательно, к b является фронталью |
|
|
|
|
|
|||||||||||
b2 |
M,K |
|
|
|
|
Пояснения к решению примера: |
||||||||||
a |
M |
2 |
1. M |
a |
a |
Ï |
2 |
M |
2 |
a |
2 |
. 2. l |
a |
|||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
||||
|
K2 |
|
|
|
a Ï2 |
l Ï2. 3. l M l b |
||||||||||
l2 |
|
|
|
l2 |
M2 |
l2 |
b2. 4. K=l |
b |
K2=l2 b2 |
|||||||
|
|
|
|
|||||||||||||
|
|
|
|
|
K1 |
b1. 5. l Ï2 |
l K |
|
|
l1 |
K1 |
|||||
|
|
|
l1 |
|
l1 |
a1 . 6. M = l a |
|
|
M1 = l1 |
a1 . |
||||||
b1 |
K1 |
M1 |
|
|
7. [M,K] |
Ï2 |
|
a,b |
= M,K |
= |
M2,K2 - |
|||||
|
a1 |
|
|
искомое расстояние определено. |
|
|||||||||||
|
|
|
|
|
||||||||||||
Рис. 5.14
Таким образом, для нахождения расстояния между скрещивающимися
прямыми одну из них целесообразно сделать проецирующей, чтобы отрезок перпендикуляра, определяющий искомое расстояние, был параллелен одной из ПП.
|
|
ПРИМЕР |
5.12. |
Заданы |
|
|
|
A2 |
a2 |
|
|
|||||||
скрещивающиеся прямые a и b |
|
|
|
|
|
M2 |
D2 |
|||||||||||
|
|
|
|
|
|
|
||||||||||||
(рис. 5.15). a,b |
- найти расстоя- |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
||||||||||
ние между этими прямыми. |
|
|
|
|
|
|
|
|
B2 |
|||||||||
|
|
Согласно приведенной выше |
|
|
|
|
|
|
|
K2 |
||||||||
рекомендации сначала прямую a |
|
x |
|
|
b2 |
C2 |
|
|
||||||||||
делают проецирующей, |
последо- |
|
|
2 |
|
|
|
|
|
|||||||||
вательно задавая две новые ПП: |
|
1 |
b1 |
|
|
|
|
|||||||||||
|
|
|
|
|
|
K |
D1 |
|||||||||||
1. Ï |
|
a |
Ï |
Ï |
|
(новая ось проек- |
x1 |
|
|
|
C1 |
|||||||
3 |
1 |
|
3 |
|
1 |
|
||||||||||||
|
x1 3 |
3 |
|
|
|
a Ï4 Ï3 |
|
A1 |
|
|
||||||||
ций |
|
a 1 ). 2. Ï4 |
|
|
|
|
|
|
|
a1 |
||||||||
(новая ось проекций |
|
x3 |
4 |
|
|
|
|
M1 |
||||||||||
x3 4 a3). |
|
|
|
|
|
|
C3 |
|
|
|
||||||||
|
|
|
|
K4 |
C4 |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
a3 |
K3 |
|
|
B1 |
|
|
|
|
|
|
|
M,K |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
D |
|
M4 |
a4 B4 A4 |
|
A |
3 |
|
|
M |
3 |
D3 |
B |
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
3 |
||||
|
|
|
|
|
|
b4 |
|
|
|
|
|
|
|
Рис. 5.15 |
b3 |
|
||

|
|
|
|
|
|
|
|
|
|
|
48 |
|
|
|
|
|
|
|
|
|
|
Для построения новых проекций прямых на каждой из них |
|||||||||||||||||
взяты две произвольные точки (A и B на a, |
C и D на b). |
|
|
||||||||||||||||
|
|
Дальнейшие рассуждения следующие: 1. a |
|
Ï4 |
[M,K] Ï4, где |
||||||||||||||
[M,K] - отрезок общего перпендикуляра к прямым a |
и b, несущий |
||||||||||||||||||
искомое расстояние (пусть M |
a, K |
b). 2. Так как [M,K] |
Ï4, то это |
||||||||||||||||
расстояние найдено: |
a,b |
= |
M,K |
= |
M4,K4 |
(M4 |
|
a4 |
[M4,K4] b4). |
||||||||||
3. K |
b |
K3 |
b3, K1 |
b1, K2 |
b2. 4. Проекция M3 |
|
точки M найдена на |
||||||||||||
a3 |
из условия [M3,K3] |
a3 (a |
Ï3 |
[M,K] |
a), а M1 |
|
и M2 - на a1 и a2 |
||||||||||||
соответственно. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
ПРИМЕР 5.13. |
Заданы скрещивающиеся прямые a и b (рис. |
||||||||||||||||
5.16). |
a,b |
|
- найти расстояние между этими прямыми. |
|
|
||||||||||||||
|
|
В |
примере |
b |
Ï2 , |
поэтому |
|
|
|
|
|
K3 |
b3 |
D3 |
|||||
проецирующей делают прямую b, |
|
|
x2 3 |
|
|
||||||||||||||
используя новую ПП |
Ï |
3 |
b (новая |
|
|
|
A3 |
M,K |
|
||||||||||
ось проекций x2 3 |
|
Для по- |
|
|
|
|
|
|
|
||||||||||
b2). |
|
|
|
|
|
a3 |
|
|
|||||||||||
строения проекций a3 и b3 на пря- |
A2 |
|
K2 |
|
|
M3 |
|||||||||||||
мых брали точки: A,B |
a и |
D |
b. |
|
|
|
|
|
|
|
B3 |
||||||||
Расстояние |
|
a,b |
равно длине от- |
|
D2 |
|
|
|
|
|
|||||||||
|
|
M |
|
|
|
|
|
||||||||||||
резка |
[M,K] |
([M,K] |
a |
|
[M,K] |
b, |
b2 |
2 |
B |
|
|
||||||||
|
a2 |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
M |
a, K |
b). Пояснения к решению : |
|
|
|
|
|
2 |
|
|
|||||||||
|
|
|
|
|
|
|
|
||||||||||||
1. В поле Ï3 - b |
Ï3 |
[M,K] |
b |
K3 |
|
a1 |
|
|
|
x1 |
2 |
||||||||
b3 |
[M,K] |
Ï3; [M,K] |
a |
[M,K] |
Ï3 |
|
A |
|
|
|
|
|
|||||||
|
[M3,K3] |
a3 |
M3,K3 |
= M,K . |
|
1 |
|
|
|
|
|
|
|
||||||
|
|
|
|
M1 |
|
B1 |
|
|
|||||||||||
2. В поле Ï2 - M2 |
a2; |
b |
Ï2 |
[M,K] |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
||||||||||||
b |
|
[M2,K2] |
b2. В поле Ï1 - M1 a1 |
|
|
|
|
|
|
|
|
||||||||
K1 |
b1. |
|
|
|
|
|
|
|
|
D1 |
|
K1 |
b1 |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 5.16 |
|
|
5.5. Определение натурального вида треугольника
Задача на определение натурального вида треугольника - ключевая задача для группы задач, в которую, в частности, входят задачи на определение натурального вида других плоских фигур, на построение биссектрисы угла между пересекающимися прямыми, центра окружности, вписанной в треугольник или описанной вокруг него, плоских фигур по заданным условиям.

49
В разделе 5.5 решение ключевой задачи осуществляется только с использованием способа введения новой ПП.
Плоская фигура проецируется на плоскость проекций в натуральную величину, если плоскость фигуры параллельна этой ПП.
Если плоская фигура расположена в проецирующей плоскости, то для определения натурального вида фигуры достаточно решить 4ОЗПЧ, используя одну новую ПП (рис. 3.19 и пояснения к нему).
Если плоская фигура расположена в плоскости общего положения 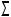 , то для того, чтобы плоскость
, то для того, чтобы плоскость 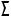 стала параллельна плоскости проекций (стала плоскостью уровня), надо последовательно задать
стала параллельна плоскости проекций (стала плоскостью уровня), надо последовательно задать
две новые ПП (сразу задать ПП параллельно плоскости |
|
|
|
нельзя, так |
|||||||||||||
как эта ПП не будет перпендикулярна ни Ï1, ни Ï2): |
|
|
|
|
|
|
|
|
|||||||||
|
1. Задают Ï3 |
перпендикулярно горизонтали h |
|
|
(новая |
ось |
|||||||||||
x1 |
3 h1 ) или фронтали f |
(новая ось x2 3 |
f2) плоскости |
, решая |
|||||||||||||
3ОЗПЧ и делая |
проецирующей. |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
2. Задают Ï4 |
Ï4 Ï3 |
(новая ось x3 |
4 |
3, где |
|
|
|
3 |
- основная |
|||||||
проекция плоскости |
), решая 4ОЗПЧ. |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
ПРИМЕР 5.14. Задан ABD (рис. 5.17), расположенный в плос- |
||||||||||||||||
кости общего положения |
. |
ABD |
- найти натуральный вид |
ABD. |
|||||||||||||
|
|
B2 |
|
|
|
A4 |
|
На 1-ом этапе в плос- |
|||||||||
|
|
|
|
ABD |
кости |
|
проводят |
гори- |
|||||||||
A2 |
h2 |
|
|
D4 |
|
|
зонталь h и задают Ï3 |
||||||||||
|
|
|
|
|
h |
Ï3 |
|
|
|
|
Ï3 |
Ï1 |
|||||
|
|
|
|
|
|
|
(новая |
ось |
проекций |
||||||||
|
D2 |
x |
4 |
|
|
|
x1 |
3 |
h |
1 |
). Найдя проек- |
||||||
|
3 |
|
|
|
|
|
|
|
|
A3, |
B3 и D3 , |
||||||
x1 |
|
|
|
|
|
|
ции точек |
|
|||||||||
2 |
|
|
|
|
|
получают |
|
основную |
|||||||||
|
D1 |
D3 |
|
|
|
проекцию |
|
|
3 |
|
плоскости |
||||||
|
h1 |
A3 |
B4 |
|
|
|
|||||||||||
|
|
|
( |
3 |
A |
, B |
3 |
, D ) . |
|
||||||||
|
|
|
|
|
|
|
|
3 |
|
|
|
|
3 |
|
|||
A1 |
|
|
|
|
|
|
|
На 2-ом этапе задают |
|||||||||
|
|
|
|
|
B3 |
Ï4 |
Ï4 |
) |
Ï3 |
(новая ось |
|||||||
|
|
|
|
|
|
x |
|
3 |
и определяют |
||||||||
|
B1 |
|
x1 |
|
|
|
3 4 |
|
|
|
|
|
вид |
тре- |
|||
|
|
3 |
|
|
натуральный |
|
|||||||||||
|
|
Рис. 5.17 |
|
угольника: |
|
|
ABD |
= |
|||||||||
=
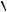 A4 B4D4
A4 B4D4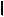 . На рис. 5.17 отмечены расстояния, откладываемые при построении проекций точки D.
. На рис. 5.17 отмечены расстояния, откладываемые при построении проекций точки D.

50
Л Е К Ц И Я 6
ПОВЕРХНОСТИ
6.1. Образование поверхности
В математике под поверхностью понимают непрерывное двухпараметрическое множество точек, координаты которых в декартовой системе координат связаны уравнением F(x,y,z)=0. Если F(x,y,z)=0 - многочлен n-ой степени, то он задает алгебраическую поверхность n-го порядка. С плоскостью такая поверхность может пересекаться по кривой порядка не выше n, а с прямой линией - не более чем в n точках.
В НГ используется преимущественно кинематический способ образования поверхности: поверхность образуется непрерывным перемещением некой линии, двигающейся в пространстве по определенному закону.
Линия, перемещаемая в пространстве и образующая при этом поверхность, называется образующей поверхности, а закон её перемещения - законом образования поверхности. Закон образования поверхности определяет единый для данной образующей способ её образования (получения) при движении и представляет собой совокупность условий, которым должна подчиняться образующая при формировании поверхности.
Все многообразие кинематических поверхностей определяется разнообразием форм образующих линий и законов образования поверхностей.
Внимание: используемые далее термины типа “образующая”, “образующие”, “эта образующая”, “проведем образующую” и т. п. относятся к различным положениям образующей.
Так как процесс перемещения образующей непрерывен, то для графических построений удобно рассматривать поверхность как непрерывную совокупность имеющих единый закон образования (получения) линий-образующих, называемую непрерывным каркасом этой поверхности. При этом образующую линию в каждом своем положении называют элементом каркаса или линией каркаса.
Пусть некая кинематическая поверхность 
 образуется непрерывным перемещением образующей a, ряд положений которой a1, a2, ..., ai, ... приведен на рис. 6.1. Линии a1, a2, ..., ai являются элементами каркаса этой поверхности.
образуется непрерывным перемещением образующей a, ряд положений которой a1, a2, ..., ai, ... приведен на рис. 6.1. Линии a1, a2, ..., ai являются элементами каркаса этой поверхности.
