
начерт
.pdf
71
7.4. Задание проецирующих поверхностей
Поверхность называется проецирующей относительно ПП, если она проецируется на эту ПП в линию, называемую основной проекцией поверхности. При ортогональном проецировании проецирующими могут быть только поверхности, несущие на себе каркас параллельных прямых: плоскость (см. лекцию 3), цилиндрическая и призматическая поверхности. Эти поверхности являются проецирующими на ПП, если их образующие перпендикулярны данной ПП. Основная проекция проецирующей поверхности обладает “собирательным” свойством - в неё проецируются все точки и линии проецирующей поверхности.
На рис. 7.18 проецирующая цилиндрическая поверхность задана элементарным чертежом, а на рис. 7.19 - основным. Образующая поверхности l Ï1, поэтому поверхность является проецирующей относительно Ï1 . Окружность Ô1 - основная проекция рассматривае-
Ï1, поэтому поверхность является проецирующей относительно Ï1 . Окружность Ô1 - основная проекция рассматривае-
мой поверхности - в Ô1 на Ï1 проецируются все точки и линии
поверхности: M  Ô
Ô M1
M1 Ô1; k, m1, m2
Ô1; k, m1, m2 Ô
Ô k1 , m11 , m21
k1 , m11 , m21 (
( )Ô1 .
)Ô1 .
На рис. 7.31 изображена прое-
цирующая на Ï2 призматическая |
|
поверхность |
{t(t,a)(ti t;ti a)}, |
a[A,B,D,A], так как |
t Ï2 . На Ï2 все |
точки и линии этой поверхности проецируются в её основную проек-
цию треугольник 2: M, a, g |
M2, |
a2, g2 ( ) 2. |
|
Заметим, что для задания проецирующих цилиндрической и призматической поверхностей достаточно было задать только их основные проекции Ô1 и 
 2 соответственно.
2 соответственно.
 B2
B2 t2
t2
M2
A2 

 2
2 a2
a2 g2
g2  D2
D2
t1 |
M1 |
|
g1 |
A1  B1
B1 a1
a1  D1
D1
Рис. 7.31

72
Л Е К Ц И Я 8
ГЛАВНЫЕ ПОЗИЦИОННЫЕ ЗАДАЧИ
В лекции 4 были рассмотрены две ГПЗ для прямых и плоскостей: 1ГПЗ - задача на пересечение линии и поверхности; 2ГПЗ - задача на пересечение двух поверхностей. В зависимости от вида пересекающихся ГО возможны три случая их расположения относительно плоскостей проекций, каждому из которых соответствует определенный алгоритм решения. В основу любого из этих алгоритмов положено условие - точка или линия пересечения принадлежат каждому из пересекающихся ГО.
8.1. Первый случай ГПЗ (ГПЗ-1)
В 1-м случае пересекаются проецирующие ГО, которыми при ортогональном проецировании могут быть прямая линия, плоскость, цилиндрическая и призматическая поверхности. Согласно алгоритму (лекция 4) в 1-м случае обе проекции точки или линии пересечения известны и их только обозначают.
На рис. 8.1 показано решение 1ГПЗ-1 с призматической поверхностью Ô Ï1 и прямой a
Ï1 и прямой a Ï2; на рис. 8.2 - 2ГПЗ-1 с цилиндрической поверхностью Ô
Ï2; на рис. 8.2 - 2ГПЗ-1 с цилиндрической поверхностью Ô Ï2 и плоскостью
Ï2 и плоскостью 
 Ï1, на рис. 8.3 - с цилиндрической Ô
Ï1, на рис. 8.3 - с цилиндрической Ô Ï2 и призматической
Ï2 и призматической 

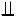 Ï1 поверхностями.
Ï1 поверхностями.
|
Ô2 |
|
k2 |
|
a2 N2 K2 |
Ô2 k2 |
|
|
|
|
|
|
|
|
a1 |
1 |
|
|
|
N1 |
|
|
|
|
k1 |
k1 |
|
1 |
|
K1 |
|
|
||
|
|
|
|
|
Ô1 |
|
|
|
|
Рис. 8.1 |
Рис. 8.2 |
Рис. 8.3 |
|
|
Пусть прямая a и поверхность Ô (рис. 8.1) пересекаются в точ- |
||||
ках K и N. Тогда K,N |
a и K,N Ô. Поэтому a2 K2 |
N2 |
(на Ï2 |
все |
точки прямой a проецируются в точку a2) и K1 =a1 |
Ô1 , |
N1=a1 |
Ô1 |
|
(в прямоугольник Ô1 - основную проекцию призматической поверхности проецируются на Ï1 все точки этой поверхности).

73
|
На рис. 8.2 k= |
Ô |
k |
k Ô. Но |
Ï1 Ô |
Ï2 k1 |
1 |
|
k2 ( )Ô2 (все точки плоскости проецируются на Ï1 |
в прямую |
1, |
||||
а |
все точки цилиндрической поверхности Ô проецируются на |
Ï2 |
|||||
в |
кривую Ô 2 ). Из |
тех |
же |
соображений на рис. 8.3 выделены |
|||
и обозначены проекции |
k1 и |
k2 линии пересечения поверхностей |
|||||
Ô и . |
|
|
|
|
|
|
|
8.2. Второй случай ГПЗ (ГПЗ-2)
Во 2-м случае один пересекающийся ГО является проецирующим, а второй непроецирующим. Алгоритм решения ГПЗ в этом случае:
1.Одна проекция точки или линии пересечения задана на чертеже.
2.Она принадлежит основной проекции проецирующего ГО и её только обозначают.
3.Неизвестная проекция точки или линии пересечения строится по её известной проекции из условия принадлежности точки или линии пересечения непроецирующему ГО.
|
|
На рис. 8.4 определены точки K и N |
||||||
|
|
пересечения кривой |
k и |
призматической |
||||
K |
k2 |
поверхности : |
K,N |
k |
и |
K,N |
. Так |
|
2 |
|
как |
Ï1, то все точки поверхности проеци- |
|||||
N2 |
|
|||||||
|
|
руются на Ï1 в треугольник |
1 - |
основную |
||||
|
|
проекцию призматической |
поверхности, и |
|||||
|
|
K1 =k1 |
1, N1 =k1 |
1 . K2 |
и N2 найдены на |
|||
|
|
k2 с использованием K1 , N1 |
и линий связи. |
|||||
N1 |
k1 |
В задаче надо решить вопрос види- |
||||||
мости |
линии |
k |
относительно Ï 2. На |
|||||
K1 |
|
участке между левым контурным ребром и |
||||||
1 |
|
точкой N кривая k не видна, поскольку не |
||||||
|
|
|||||||
Рис. 8.4 |
|
видна относительно Ï2 точка N. На участке |
||||||
|
|
между |
точками |
N и K кривая |
находится |
|||
внутри непрозрачной поверхности и также не видна. На участке
между точкой K и правым контурным ребром кривая видна, |
так как |
|||||||
относительно Ï2 |
точка K видна. |
K и N пересечния прямой a с |
||||||
На рис. 8.5 построены точки |
||||||||
отсеком |
конической |
поверхности |
вращения Ô{t(t,j;t |
j)(ti |
=t j)}. |
|||
K,N a |
a |
Ï2 |
a 2 |
K2 |
N2 . |
Проекции K1 и N1 находили |
||
по их известным проекциям |
K2 и |
N 2 |
из условия, что |
K,N |
Ô . |
|||

74
t2 |
F2 j2 |
||
R |
|
||
a2 Ê2 N2 E2 |
m2 |
||
a1 |
|||
|
|
||
t |
F1 E1 |
|
|
1 |
|
N1 |
|
|
|
||
j1 |
Ê1 |
m1 |
|
|
|
||
Рис. 8.5
Ô - поверхность вращения, поэтому K1 и N1 найдены с использованием окружности m
радиуса R, принадлежащей |
поверхнос- |
||
ти и |
проходящей |
через искомые точки: |
|
K1 =m1 |
a1 и N1 =m1 |
a1. |
|
Относительно |
Ï1 виден |
участок NK |
|
прямой, находящейся внутри поверхности - тончайшей оболочки. На участке EN прямая не видна: она находится ниже поверхности, поскольку точка E прямой ниже конкурирующей с ней точки F поверхности (см. в поле Ï2 на E2 и F2).
На рис. 8.6 построены точки K и N пересечения цилиндрической поверхности Ô{t(t, m)(ti 
 m; ti
m; ti 
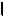 t)} с прямой a. Так как a
t)} с прямой a. Так как a Ï2, то K2 и N2 известны: K2
Ï2, то K2 и N2 известны: K2 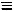 N2
N2 a2. K1 и N1 найдены по их известным проекциям K2 и N2 из условия, что K,N
a2. K1 и N1 найдены по их известным проекциям K2 и N2 из условия, что K,N Ô , с использованием прямолинейных образующих t1 и t2 (поверхность Ô - линейчатая). Образующие построены по данному закону образования, начиная с проведения t21
Ô , с использованием прямолинейных образующих t1 и t2 (поверхность Ô - линейчатая). Образующие построены по данному закону образования, начиная с проведения t21  t22 через a2 параллельно t2.
t22 через a2 параллельно t2.
Прямая a пересекает цилиндрическую поверхность в её нижней части (см. в поле Ï2 на a 2 ). Поэтому относительно Ï 1 через отверстие (окружность m) виден небольшой отрезок прямой за точкой N.
m2
t2
t22 t12
t12
a2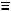 N2
N2 K2
K2
a1
t21 K1
N1
t11 |
t1 |
m1
Рис. 8.6

|
|
75 |
Далее приводятся несколько примеров решения 2ГПЗ-2. |
||
ПРИМЕР 8.1. |
Построить линию пересечения k сферы |
|
Ô{m(m,j;Cm |
j)(mi =m |
j)} и цилиндрической поверхности вращения |
{t(t,j1 ;t |
j1 )(ti =t |
j1)}, показав построение её характерных точек. |
Определить видимость линии k и взаимную видимость контурных линий пересекающихся поверхностей (рис. 8.7).
72 |
82 |
j2 j21 |
12 |
||
q2 |
42 |
|
A |
M2 |
|
m2 2 |
|
|
|
|
k2 |
c2 |
|
|
q1 |
|
|
m1 |
|
|
Cq |
j |
1 |
|
|
|
1 |
|
|
|
8 |
1 |
61 |
|
|
|
1 |
|
1 |
|
|
A1 |
|
|
|
|
1 |
71 |
41 |
|
|
j1 |
|
|
|
|
|
||
c1
M1
Рис. 8.7
t2

 22
22
52
32

 1
1 k1
k1
21
Проекция k1 линии k из-
вестна: k=Ô





 Ï1 (t
Ï1 (t Ï1)
Ï1)
 k1
k1

 1 (в окружность
1 (в окружность 
 1 на Ï1 проецируются все точки поверхности
1 на Ï1 проецируются все точки поверхности 
 ).
).
Проекцию k2 приближенно проводят через фронтальные проекции некоторого числа точек линии k. Каждую из этих проекций строят так: на k1 берут горизонтальную проекцию точки и ищут её фронтальную проекцию из условия принадлежности точки сфере - с помощью окружности q. ГА построения фронтальной проекции M2 произвольной точки M k :
k :
51 t1 |
1. |
M1 |
k1 . |
|
2. |
q1 |
M1, Cq1 j1. |
|
3. |
A1 |
=q1 m1. |
31 |
4. |
A2 |
m2. |
|
5. |
q2 |
A2 , q2 j2 . |
|
6. |
M2 |
q2 . |
Характерные точки линии пересечения - точки, расположенные на контурных линиях пересекающихся поверхностей; “крайние” точки кривой - самая верхняя, самая левая и т. п.; точки, определяющие оси кривой, и т. д. В задаче на рис. 8.7 точки 1, 2, 3 расположены на контурных линиях сферы, причем точка 3 - самая нижняя точка кривой; самая левая 4 и правая 5 точки кривой лежат
76
на контурных образующих цилиндрической поверхности; 6 - самая верхняя точка кривой (проекция 62 на рис. 8.7 не обозначена). Проекции 12, 22 найдены на меридиане, а 32 - на экваторе сферы; проекции 42, 52, 62 построены подобно проекции M2.
Количество точек, используемых для построения k2 , должно быть таким, чтобы по ним можно было однозначно определить и с достаточной степенью точности вычертить эту проекцию.
Границей видимости точек поверхности относительно ПП являются крайние относительно этой ПП контурные линии поверхности. Поэтому видимость линии пересечения поверхностей может меняться только в точках этой линии, расположенных на крайних относительно рассматриваемой ПП контурных линиях одной из поверхностей. Границей видимости точек сферы относительно Ï2 является её меридиан m - при взгляде на Ï2 видны все точки линии k, лежащие перед меридианом (точки 1, 4, M, 3, 5, 2). Видимость точек цилиндрической поверхности относительно Ï2 меняется на крайних её образующих, проходящих через точки 4 и 5, - при взгляде на Ï2 видны все точки линии k, лежащие в передней части поверхности (точки 4, M, 3, 5). В результате относительно Ï2 видимыми будут те точки линии k, которые одновременно видны и для сферы, и для цилиндрической поверхности - точки 4, M, 3, 5.
В учебном курсе принята модель: поверхности при пересечении образуют единую фигуру и друг в друга не проникают. Так левая контурная образующая цилиндрической поверхности существует только до точки 4, в которой она пересекает сферу, правая - до точки 5, а меридиан m сферы не существует между точками 1 и 2. Проекции несуществующих контурных линий на чертеже либо не наносят, либо вычерчивают тонкой сплошной линией.
Определяя взаимную видимость контурных линий пересекающихся поверхностей, удобно использовать конкурирующие точки. Пусть надо определить: относительно Ï2 видна левая образующая цилиндрической поверхности от точки 7 до точки 4 или меридиан m сферы от точки 8 до точки 1, где 7 и 8 - конкурирующие точки контурной образующей цилиндрической поверхности и меридиана сферы. Ответ: точка 7 цилиндрической поверхности ближе к наблюдателю точки 8 сферы (см. на 71 и 81 на рис. 8.7), поэтому относительно Ï2 видна часть контурных образующих цилиндрической поверхности, а часть меридиана сферы не видна.

77
На рис. 8.8 построена линия пересечения k цилиндрической
поверхности Ô{l(e,l)(li e;li
e;li
 l)} с призматической
l)} с призматической 
 {t(a,t)(ti
{t(a,t)(ti  a;ti
a;ti 
 t)},
t)},
a[A,B,D,A]. |
|
B2 |
l22 |
|
|
e2 |
|
H2 |
R2 |
|
|
|
i |
4 |
|||
|
|
|
N2 |
l2 |
l2 |
|
22 |
M2 |
|
|
|
12 |
|
l2 l12 |
|||
|
|
E2 F2 |
C2 Q2 |
32 k2 |
2 a2 |
|
l |
3 |
A |
t L G |
D |
2 |
t1 |
P T 4 |
||||
|
|
2 |
2 |
2 |
2 |
2 |
|
2 |
2 |
2 |
2 |
|
|
|
|
t1 |
|
|
|
|
|
31 |
41 |
|
|
|
l1 |
|
E1 |
|
|
C1 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|||
11 |
l1i |
|
M1 |
|
N1 |
|
|
|
|
|
|
|
|
|
L1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R1 |
P1 |
|
|
|
|
|
||
e1 |
|
|
H1 |
|
|
|
|
|
|
|||
3 |
2 |
|
G |
|
|
|
T |
|
|
l41 |
|
|
l1 |
l1 |
|
|
|
|
|
|
|
|
|
||
|
|
|
1 |
|
|
|
1 |
|
|
|
|
|
|
21 |
|
|
1 |
1 |
|
|
|
|
l11 |
|
|
|
|
|
M1 |
N1 |
|
|
|
|
|
|
|
|
|
|
|
F1 |
|
|
Q1 |
t11 |
|
|
|
|
|
|
|
|
A1 |
|
B1 |
a1 |
D1 |
|
|
|
|
|
|
|
|
Рис. 8.8 |
|
|
|
|
|
|
|
|
|
Грань AD призматической поверхности |
пересекает цилинд- |
|||||||||||
рическую поверхность |
Ô по отрезкам двух образующих (грань AD |
|||||||||||
параллельна образующим поверхности |
Ô ), а грани BA и BD - по |
|||||||||||
дугам эллипсов, имеющих общие точки с отрезками образующих на
ребрах t и t1 |
поверхности . |
|
|
Призматическая поверхность |
Ï2 (t Ï2). Поэтому все её точ- |
||
ки проецируются на Ï2 в треугольник |
2 |
a2 и проекция k2 линии k |
|
известна: k2 |
2 (k2 - ломаная H2A2D2R2). |
Для построения проекции |
|

78
k1 ищут горизонтальные проекции нужного числа точек линии k, используя для этого их фронтальные проекции и образующие li ци-
линдрической поверхности. Например, проекция |
M1 произвольной |
||||
точки M k |
найдена согласно следующему алгоритму: |
||||
1. |
M2 |
k2. |
4. |
1 1 |
e1. |
2. |
l2i |
M2; l2i l2. |
5. |
l1i |
11; l1i l1 . |
3. |
12 = l2 e2. |
6. M1 |
l 1i . |
||
Проекцией M2 на цилиндрической поверхности в общем случае задаются две точки - собственно точка M(M1,M2) и точка M1(M11,M2). Точка M li, а точка M1
li, а точка M1 l4, причем l2i
l4, причем l2i  l42. На образующих li и l4 еще расположены точки N и N1 второго эллипса.
l42. На образующих li и l4 еще расположены точки N и N1 второго эллипса.
Характерные точки линии k - точки L, G, P и T, расположенные на ребрах t и t1 призматической поверхности, и точки H, E, F, R, Q и C, принадлежащие контурным образующим цилиндрической поверхности. Проекции E1 , C1 , F1 , Q1 , H1 , R1 найдены на горизонтальных проекциях l1, l11 и l21 этих образующих по известным фронтальным проекциям точек с помощью линий связи. Проекции L1, G1, P1, T1 построены аналогично проекции M1 (см. приведенный выше алгоритм её определения). Точки H, E, F, R, Q и C принадлежат эллипсам, а точки L, G, P и T - общие точки эллипсов и отрезков [L,P] и [G,T] (по этим отрезкам цилиндрическая поверхность пересекается гранью AD призматической поверхности).
В результате пересечения не будут существовать ребра призматической поверхности t между точками L, G и t1 - между точками P, T; контурные относительно Ï1 образующие цилиндрической поверхности l между точками E, C и l1 между точками F, Q и контурная относительно Ï2 образующая этой поверхности l2 между точками H, R.
Относительно Ï1 видны все точки призматической поверхности, расположенные в верхних гранях BA и BD, то есть целиком видны обе дуги эллипсов и не видны отрезки образующих [L,P] и [G,T]. У цилиндрической поверхности относительно Ï1 видны все её точки, лежащие выше контурных относительно Ï1 образующих l и l1, то есть только части дуг эллипсов FM1HME и QN1RNC, и не видны дуги эллипсов GF, LE и TQ, CR, а также отрезки указанных образующих. Окончательная видимость линии k относительно Ï1 совпадает с видимостью линии k на цилиндрической поверхности.

79
Для определения видимости контурных линий пересекающихся поверхностей на одном из участков использованы конкурирующие относительно Ï1 точки 3 образующей l цилиндрической поверхности и 4 ребра t1 призматической поверхности. Так как точка 3 выше точки 4 (см. на 32 и 42), то на рассматриваемом участке видна до точки C образующая l и не видно до точки P ребро t1 . В данном примере вопрос видимости контурных линий решался ещё для трех аналогичных участков фигуры, полученной в результате пересечения поверхностей.
Л Е К Ц И Я 9
ГЛАВНЫЕ ПОЗИЦИОННЫЕ ЗАДАЧИ (продолжение)
9.1. Конические сечения
При пересечении конической поверхности плоскостью в зависимости от их взаимного положения линией пересечения может быть та или иная кривая второго порядка. На рис. 9.1 - 9.3 это демонстрируется на примере пересечения плоскостью конической поверхности вращения.
 2
2
1 |
2 |
1 |
|
|
Ã1
Ã2
Рис. 9.1 |
Рис. 9.2 |
Рис. 9.3 |
Если плоскость пересекает все образующие конической |
||
поверхности, не пересекает её вторую полость и < |
(рис. 9.1), то |
|
в сечении получают эллипс (Ã1 ) или его частный случай - окружность (Ã2). Если плоскость параллельна одной образующей конической поверхности, не пересекает её вторую полость и  =
=  (рис. 9.2), то в сечении получают параболу (
(рис. 9.2), то в сечении получают параболу (  1 ) или её частный случай -
1 ) или её частный случай -

80
пару совпадающих прямых ( 2). Если плоскость параллельна двум образующим конической поверхности, пересекает обе её полости и
2). Если плоскость параллельна двум образующим конической поверхности, пересекает обе её полости и  >
> (рис.9.3), то в сечении получают гиперболу (
(рис.9.3), то в сечении получают гиперболу ( 1 ) или её частный случай - пару пересекающихся прямых (
1 ) или её частный случай - пару пересекающихся прямых ( 2) (рис. 9.3).
2) (рис. 9.3).
ПРИМЕР 9.1. Построить линию пересечения k конической поверхности Ô{t(T,m)(ti T;ti
T;ti m)} и плоскости
m)} и плоскости  (рис. 9.4).
(рис. 9.4).
Линия k в примере является эллипсом, поскольку плоскость  пересекает все образующие конической поверхности и не пересекала бы её вторую полость при наличии таковой.
пересекает все образующие конической поверхности и не пересекала бы её вторую полость при наличии таковой.
|
|
Проекция k2 |
линии k известна: k |
|
Ï2 |
k2 |
|
2. Проекцию |
||||||||
k |
|
приближенно |
проводят через |
проекции |
Mi |
ряда |
|
точек |
Mi |
k. |
||||||
1 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
M1i |
|
определяют по проекциям M2i |
k2 и условию Mi Ô согласно ГА: |
|||||||||||||
|
|
|
|
|
|
2 |
|
T2 |
|
1. |
M2i |
|
k2. |
|
|
|
|
|
|
|
|
k2 |
t2 |
t21 |
|
2. ti |
M i ,T . |
|
|||||
|
|
|
|
i |
|
|
|
|||||||||
|
|
|
|
M2 |
|
|
|
|
|
|
2 |
|
2 |
2 |
|
|
|
|
|
2 |
22 |
|
12 |
|
|
3. |
A2 =t2i |
m2. |
|
|
|||
t |
i |
|
|
|
|
|
4. |
A1 |
m1. |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
3 |
4 |
|
|
5. t1i |
|
T1,A1. |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
2 |
2 |
|
|
|
|
|
|
|
|
|
A2 |
m2 |
|
t3 |
t4 |
|
|
|
6. M1i |
|
t1i . |
|
|
|
|||
|
|
|
|
|
2 |
2 |
|
|
|
Так строят нужное число |
||||||
|
|
|
|
|
|
|
|
|
|
|||||||
m1 |
|
|
k1 |
|
4 |
|
произвольных точек линии k1 . |
|||||||||
|
|
|
|
41 |
|
|
Характерными |
точками |
||||||||
|
|
|
|
|
|
t1 |
|
|
||||||||
|
|
t11 |
t12 |
21 |
|
11 |
|
|
линии пересечения являются |
|||||||
|
|
|
|
T1 |
точки 1 и 2, расположенные |
|||||||||||
|
|
|
|
M1i |
|
|
на контурных относительно Ï2 |
|||||||||
|
|
|
|
|
|
|
|
t3 |
образующих t1 |
и t2 |
коничес- |
|||||
A1 |
i |
|
|
31 |
|
1 |
кой поверхности (1 также са- |
|||||||||
|
|
|
|
|||||||||||||
t1 |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
мая верхняя и правая точка |
|||||||
|
|
|
|
Рис. 9.4 |
|
|
линии k, а 2 - самая нижняя |
|||||||||
|
|
|
|
|
|
и левая), и точки 3 и 4, ле- |
||||||||||
|
|
|
|
|
|
|
|
|
||||||||
жащие на контурных относительно Ï1 |
образующих t3 и t4. Точки 3 |
|||||||||||||||
и 4 искали так: по известным проекциям |
t13 |
и t 41 |
строили их |
|||||||||||||
проекции t32 и t42 |
и находили 32=t23 |
k2; 31 |
t13; 42=t42 |
|
k2; 41 |
t41 |
(в |
|||||||||
примере t23 |
t42 и 32 |
42). |
|
|
|
|
|
|
|
|
|
|
||||
