
начерт
.pdf
61
ПРИМЕР 7.1. Задана призматическая поверхность
Ô{l(l,a)(li 
 a, li
a, li l)}, a[A,B,D,E] (рис. 7.5). 1. Построить проекции произ-
l)}, a[A,B,D,E] (рис. 7.5). 1. Построить проекции произ-
вольной точки M Ô . 2. Построить проекцию N2 точки N
Ô . 2. Построить проекцию N2 точки N  Ô по известной проекции N1 . 3. Определить, принадлежит ли поверхности Ô заданная точка F.
Ô по известной проекции N1 . 3. Определить, принадлежит ли поверхности Ô заданная точка F.
|
l2 |
i |
|
|
l2 |
A |
M2 |
|
2 |
|
|
|
12 |
N2 |
|
B2 |
|
|
2 |
|
|
a2 |
2 |
|
D2 |
|
|
|
|
|
a1 |
D1 |
|
|
|
|
B1 |
21 |
|
N1 |
|
|
11 |
|
A1 |
M1 |
l1i |
l1
Рис. 7.5
Произвольную точку M строят с помощью произвольной образую-
|
|
|
щей li |
: |
|
|
|
|
|
|
|
|
|
|
|
|
||
l12 |
|
|
1. li |
l |
|
li |
a |
. |
4. li |
l |
2 |
li |
1 . |
|||||
|
l22 |
|
|
|
1 |
1 |
|
|
1 |
1 |
|
|
2 |
|
2 |
2 |
||
F2 |
|
2. 11 =l1i a1. |
|
|
5. |
M1 |
|
|
l1i. |
|
||||||||
3 |
|
|
3. |
1 |
2 |
|
a |
2 |
. |
|
|
6. |
M |
|
|
li. |
|
|
2 |
E2 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
2 |
|
||
|
|
|
Проекцию N2 точки N находят |
|||||||||||||||
|
|
|
с использованием образующей l 1 , |
|||||||||||||||
31 |
E1 |
|
проходящей через точку N: |
|
|
|
|
|||||||||||
|
1. l11 |
l1 |
|
l11 |
N1. |
4. |
l12 l2 l12 22. |
|||||||||||
l11 |
|
|
|
|||||||||||||||
|
l2 |
2. 21 =l11 |
|
a1. |
|
|
5. |
N |
2 |
|
|
l1. |
|
|||||
F |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
||
|
1 |
|
3. |
22 |
a2. |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
Для |
определения |
принадлежности |
|||||||||||||
точки F поверхности Ô делается попытка построить образующую l2 , проходящую через точку F:
1. l22 l2 l22 F2. 2. 32=l22 a2. |
3. 31 a1. |
4. l12 l1 l12 31. |
Вывод: F1  l21
l21  F
F l2
l2  F
F Ô.
Ô.
7.1.3. Коническая и пирамидальная поверхности
Формула конической поверхности имеет вид:
Ô{l(a,S)(li  a, li
a, li  S)}. Если a кривая линия, то формула определяет коническую поверхность, если a ломаная линия, то пирамидальную (в обоих случаях a и S не лежат в одной плоскости), если a прямая линия, то плоскость. Точку S называют вершиной поверхности.
S)}. Если a кривая линия, то формула определяет коническую поверхность, если a ломаная линия, то пирамидальную (в обоих случаях a и S не лежат в одной плоскости), если a прямая линия, то плоскость. Точку S называют вершиной поверхности.
На рис. 7.6 приведен элементарный чертеж конической поверхности, на рис. 7.8 - пирамидальной поверхности (направляющая a - треугольник ABDA), на рис. 7.7 - основной чертеж отсека конической поверхности, а на рис. 7.9 - отсека пирамидальной поверхности.

62
|
|
S2 |
|
|
l23 |
S2 |
|
a2 |
a2 |
|
|
||||
|
|
l21 |
|
||||
|
|
|
|
|
l2 |
||
|
|
|
|
|
|
2 |
|
|
|
S1 |
|
|
l42 |
S1 |
|
|
|
|
|
|
l12 |
||
|
|
|
|
|
|
||
a1 |
|
a1 |
|
l11 |
|
||
|
|
Рис. 7.6 |
|
|
Рис. 7.7 |
|
|
|
|
S 2 |
|
M2 |
|
S 2 |
|
|
|
|
|
|
|
||
A2 |
|
|
A2 |
|
|
|
|
a |
|
B2 |
|
12 |
B2 |
|
|
2 |
D 2 |
l2i |
D2 |
||||
|
|
a2 |
|||||
|
|
|
|||||
|
|
D1 |
li |
11 |
|
D1 |
|
A1 |
|
|
1 |
M |
|
||
|
|
|
|
|
|||
|
|
A1 |
|
1 |
|
||
|
|
S 1 |
|
|
S 1 |
||
a 1 |
|
a 1 |
|
B1 |
|||
|
|
B1 |
|
|
|
||
|
|
Рис. 7.8 |
|
|
Рис. 7.9 |
|
|
На элементарных чертежах поверхностей заданы элементы их определителей. Контурными линиями отсека конической поверхности (рис. 7.7) являются: линия обреза кривая a, вершина S, образующие l1 и l2, а также образующие l3 и l4 - линии касания поверхности проецирующими лучами, перпендикулярными Ï2 и Ï1 соответственно. Контурные линии отсека пирамидальной поверхности - линия обреза ломаная a, точка S и ребра поверхности AS, BS и DS.
Коническая и пирамидальная поверхности в общем случае имеют две полости, простирающиеся в бесконечность от вершины S в обе стороны. На рис. 7.7 и 7.9 показано только по одной “нижней” полости поверхностей.

63
На рис. 7.9 задана произвольная точка M пирамидальной поверхности, для чего строилась её произвольная образующая li:
1. li |
S |
1 |
|
li |
a |
1 |
. |
4. |
li |
|
S |
2 |
,1 . |
|||
|
|
1 |
|
|
1 |
|
|
|
2 |
|
2 |
|||||
2. |
11 |
=l1i |
|
|
a1. |
|
|
|
5. |
M1 |
l1i . |
|||||
3. |
1 |
2 |
a |
2 |
. |
|
|
|
6. |
M |
2 |
li. |
||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|||||
7.1.4. Поверхности Каталана
Поверхности Каталана - это линейчатые поверхности с двумя на- правляющими и плоскостью параллелизма: Ô{t(b,d,Ã)(ti
 b, ti
b, ti d, ti
d, ti
 Ã)}. Все образующие этих поверхностей пересекают обе направляющие
Ã)}. Все образующие этих поверхностей пересекают обе направляющие
ипараллельны плоскости параллелизма.
Взависимости от формы направляющих образуются различные поверхности: если направляющие скрещивающиеся прямые, то поверхность называется гиперболический параболоид (косая плоскость); если одна направляющая кривая линия, а вторая прямая, то поверхность называется коноид; если обе направляющие кривые линие, то поверхность называют цилиндроидом. Элементарные чертежи гиперболического параболоида, коноида и цилиндроида показаны соответственно на рис. 7.10 - 7.12.
b2 |
d2 |
b2 |
d2 |
b2 |
d2 |
b1 |
d1 |
b1 |
d1 |
b1 |
d1 |
Ã1 |
|
Ã1 |
|
Ã1 |
|
|
Рис. 7.10 |
|
Рис. 7.11 |
|
Рис. 7.12 |
|
На рис. 7.13 приведен основной чертеж отсека гиперболичес- |
||||
кого параболоида Ô{t(a, b, |
Ï2)(ti a b; ti |
)}, границами которо- |
|||
го являются линии a, b и образующие t1 и t2, проходящие соответственно через точки A, B a. Для получения чертежа сначала строят
a. Для получения чертежа сначала строят
достаточно плотный дискретный |
каркас образующих ti , включая |
||
образующие t1 A и t2 |
B. В результате определяют отрезки линий |
||
обреза отсека: [A,B] |
a, [D,E] |
b, [A,D] t1, [B,E] |
t2, и получают |
возможность провести проекцию |
p2 параболы p |
как огибающую |
|

проекций t2 образующих t i. Парабола p - линия касания поверхности гиперболического параболоида проецирующими лучами, перпендикулярными Ï2 .
64
B2 |
|
ð |
2 |
|
D2 |
|
|
|
|
|
|
ti |
|
|
|
|
b2 |
2 |
|
|
|
|
|
a2 |
|
2 |
E2 |
|
|
|
A2 |
t |
|
|
|
|
t1 2 |
|
1 |
||
|
A1 |
2 |
|
|
|
1 |
|
|
|
t1 |
|
ti |
|
|
|
|
D1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
a1 |
|
|
|
|
b1 |
|
|
t12 |
|
|
|
B1 |
|
|
E1 |
Рис. 7.13 |
|
|
|
|
|
||
7.2. Поверхности вращения
7.2.1. Образование поверхностей вращения
Поверхность вращения Ô образуется при вращении вокруг неподвижной оси j какой-то образующей линии a:
Ô{a(a,j)(ai =a |
j)} (рис. 7.14). |
m3 |
j |
||
При вращении линии a вокруг j точки |
|||||
|
|
||||
образующей a вращаются вокруг оси j по |
|
|
|||
окружностям, называемым параллелями. |
|
k1 |
|||
Так, при вращении точки Ki |
a образуется |
|
m1 |
||
параллель mi. Плоскости параллелей пер- k |
Mi |
||||
пендикулярны оси вращения. Поэтому на Ki |
|
||||
ПП, перпендикулярную оси, параллели |
|
mi |
|||
проецируются в окружности, а на другую a |
|
||||
ПП - в отрезки прямых. В этой связи точку |
|
|
|||
M на поверхности вращения в общем |
|
|
|||
случае строят |
с помощью |
окружности |
|
|
|
(параллели) mi |
согласно ПА (рис. 7.14): |
|
m2 |
||
 . mi
. mi  Ô.
Ô.
 . M
. M  mi.
mi.
Параллель m1 наименьшего радиуса называют горлом, а наибольшего - экватором (m2). Параллель m3- граница или линия обреза отсека. Плоская кривая, расположенная в плоскости, проходящей через ось вращения, называется меридианом поверхности (кривая a,

65
контурные кривые k и k 1 ). Меридиан, лежащий в плоскости, параллельной ПП, называют главным. При задании поверхности вращения элементарным чертежом удобно, чтобы её образующая являлась главным меридианом.
7.2.2. Поверхность вращения общего вида
Поверхность вращения общего вида образуется при вращении вокруг оси произвольной кривой k. Формула поверхности:Ô{k(k,j)(ki=k j)}. На рис. 7.15 задан элементарный чертеж поверхности вращения общего вида, а на рис. 7.17 - основной чертеж отсека этой поверхности с границами m1 и m2. На основном чертеже главные мериди-
j)}. На рис. 7.15 задан элементарный чертеж поверхности вращения общего вида, а на рис. 7.17 - основной чертеж отсека этой поверхности с границами m1 и m2. На основном чертеже главные мериди-
j2
|
j2 |
|
j2 |
|
|
m1 |
|
|
|
|
|
|
|
k2 |
|
k2 |
q2 |
|
k2 |
2 |
|
|
m23 |
||||
|
|
12 |
M2 |
|
m42 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
k2 |
k1 |
|
|
|
|
m2 |
m11 |
|
|
|
|
2 |
|
|
|
j1 |
k1 |
M1 |
|
m21 |
m31 |
|
|
|
|
k |
||
|
|
|
|
|
1 |
|
Рис. 7.15 |
11 |
j1 Cq1 q |
|
|
k11 |
|
|
|
1 |
4 |
|||
|
|
|
|
j1 |
||
|
|
|
|
|
m1 |
|
|
|
|
Рис. 7.16 |
|
|
Рис. 7.17 |
аны k и k1 |
являются линиями касания поверхности проецирующими |
|||||
лучами, перпендикулярными Ï2, а горло m 3 и экватор m4 - пер-
пендикулярными Ï1 |
(проекции m23 |
и m42 обычно не показывают, так |
как относительно Ï |
m3 и m4 не являются контурными линиями). |
|
2 |
|
|
На рис. 7.16 решается ОПЗ: определяют, принадлежит ли рас- |
||
сматриваемой поверхности точка |
M(M1 ,M2 ). Для этого делается |
|
попытка |
построить |
параллель q поверхности, на которой может |
||||||||||||||||||||
располагаться точка M: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
1. q M |
,Cq |
j |
. |
2. 1 |
1 |
=q |
1 |
k . |
3. 1 |
2 |
k . |
4. |
q |
2 |
1 |
2 |
, q |
2 |
j |
2 |
. |
|
1 |
1 |
1 |
1 |
|
|
|
1 |
|
2 |
|
|
|
|
|
|
|||||||
Вывод: M1 q1
q1  M2
M2 q2
q2  M
M  q; M
q; M  q
q  q
q Ô
Ô  M
M  Ô .
Ô .

66
7.2.3. Линейчатые поверхности вращения
Линейчатая поверхность вращения |
образуется при враще- |
|||
нии вокруг оси j прямой l: Ô{l(l,j)(li =l |
j)}. Если |
l j, то образуется |
||
цилиндрическая поверхность вращения, |
если l |
j - коническая по- |
||
верхность вращения, если l |
j - |
однополостный гиперболоид |
||
вращения.
На рис. 7.18 приведен элементарный чертеж цилиндрической поверхности вращения, на рис. 7.19 - основной чертеж отсека этой
поверхности, ограниченного окружностями m1 |
и m2 (l1 и l2 |
- линии ка- |
|||||||
сания поверхности проецирующими лучами, |
перпендикулярными Ï2). |
||||||||
j2 |
|
|
|
j2 |
|
m21 |
|
|
j2 |
l2 |
1 |
M2 |
|
l2 |
|
l2 |
|||
|
|
l2 |
|
|
|
|
|||
|
|
|
|
|
|
l2 |
|
|
|
|
|
k2 |
|
|
|
m22 |
|
|
|
|
|
|
|
|
Ô m1 |
m2 |
k |
|
|
|
|
l11 |
j |
|
1 |
1 |
1 |
1 |
|
|
|
1 |
|
|
|
l1 |
|
||
j1 |
|
|
|
|
2 |
|
|
||
l1 |
|
|
|
|
|
j1 |
|||
|
|
|
|
l1 |
|
|
|||
|
|
|
M1 |
|
l1 |
|
|
|
|
Рис. 7.18 |
|
Рис. 7.19 |
|
|
Рис. 7.20 |
||||
Чертежи конической поверхности вращения и примеры решения ОПЗ - см. разделы 6.3.1 и 6.3.2, рис. 6.5 и 6.7.
Однополостный гиперболоид вращения можно получить также вращением гиперболы вокруг её мнимой оси. Эта поверхность широко используется в инженерной практике: телевизионная башня известного ученого и инженера Шухова В.Г. на Шаболовке, сооруженная из каркасов однополостных гиперболоидов, градирни (трубы) ТЭЦ имеют такую форму и т. д.
На рис. 7.20 представлен элементарный чертеж однополостного гиперболоида вращения - заданы скрещивающиеся прямые l (образующая) и j (ось вращения). На рис. 7.21 приведен основной чертеж отсека рассматриваемой поверхности, образованный вращением отрезка [A,B] образующей l. Линиями обреза отсека являются окружности m1 и m2 , проходящие через точки A и B соответственно.

|
|
|
|
67 |
|
|
|
|
|
Ветви g1 |
и g2 гиперболы на чертеже |
|
B2 |
j2 |
m22 |
|
|||
- |
линии |
касания поверхности |
|
|
|
|
|
||
проецирующими лучами, перпенди- |
|
|
|
m23 |
|
||||
кулярными |
Ï2 , а горло m - перпен- |
|
|
|
|
||||
|
|
|
m2i |
|
|||||
дикулярными Ï1 . |
|
|
|
|
|
||||
g22 |
Для построения проекций g21 и |
g |
1 |
|
g |
2 |
|||
ветвей гиперболы строят доста- |
2 |
|
2 |
||||||
|
|
|
|||||||
точно плотный каркас |
параллелей |
|
|
m21 |
A2 |
|
|||
mi |
Ô (включая m1 , m2, m3), которые |
|
|
|
|||||
на Ï1 проецируются в окружности, а |
|
2 |
1 |
l2 |
|
||||
на Ï2 - в отрезки прямых. Проекции |
|
m1 |
m1 |
|
i |
||||
g21 |
и g22 проводят через крайние ле- |
g11 |
|
|
A1 m1 |
||||
вые и правые точки отрезков m2i . |
|
|
|
g21 |
|||||
|
|
7.2.4. Торы |
|
|
|
|
|
|
|
|
Поверхность тора Ô получает- |
|
|
|
|
|
|||
ся при вращении окружности m или |
|
|
j1 |
|
|
||||
её дуги вокруг оси j, причем |
|
|
|
|
|||||
|
B1 |
|
|
||||||
образующая окружность m и ось j |
l1 |
|
|
m13 |
|||||
расположены в одной плоскости: |
|
|
|||||||
Ô{m(m,j; m,j |
Ã)(mi =m |
j)}. |
|
|
|
|
|
||
|
Если окружность |
m и ось j не |
|
|
Рис. 7.21 |
|
|
||
имеют общих точек, то тор называ- |
|
|
|
|
|||||
|
|
|
|
|
|||||
ют открытым или кольцом; если окружность m и ось j |
касаются |
||||||||
(m j), то образуется закрытый тор с одной конической точкой; если ось j пересекает окружность m (m
j), то образуется закрытый тор с одной конической точкой; если ось j пересекает окружность m (m
 j), то образуется закрытый тор с двумя коническими точками, называемый также пересекающимся тором. Элементарные чертежи перечисленных торов изображены
j), то образуется закрытый тор с двумя коническими точками, называемый также пересекающимся тором. Элементарные чертежи перечисленных торов изображены
соответственно на рис. 7.22 - 7.24.
j2 j2 j2
m2 |
m2 |
m2 |
m1 |
m1 |
m1 |
j1 |
j1 |
j1 |
|
Рис. 7.22 |
Рис. 7.23 |
Рис. 7.24 |

68
На рис. 7.25 представлен основной чертеж открытого тора, а на рис. 7.26 - пересекающегося. Контурными линиями открытого
тора относительно Ï1 |
являются окружности q1 экватора и q2 |
горла, |
а относительно Ï - |
образующие окружности m и m1 , а |
также |
2 |
|
|
окружности (параллели) q3 и q4, получаемые при вращении верхней и нижней точек образующей окружности m. Контурными линиями пересекающегося тора являются аналогичные линии.
1 |
q23 |
j2 |
j2 |
q2 |
m2 |
|
|
m2 |
|
|
|
|
M2 |
|
q21 |
|
|
|
m2 |
q42 |
|
|
|
|
|
|
q22 |
|
|
q11 |
|
|
|
|
|
|
|
m1 |
m1 |
|
|
j1 |
M1 |
|
m11 |
|
q21 |
j1 |
|
|
|
|
q1 |
|
|
|
|
|
|
|
|
|
q13 q41 |
|
Рис. 7.25 |
|
|
Рис. 7.26 |
|
Частным случаем пересекающегося тора, у которого центр Cm образующей окружности расположен на оси вращения, является сфера. Формулу сферы часто записывают так: Ô{m(m,j;Cm  j)(mi =m
j)(mi =m j)}.
j)}.
На рис. 7.27 и 7.28 показаны её соответственно элементарный и основной чертежи. На элементарном чертеже задана образующая m - главный меридиан и ось j. Контурными линиями сферы на её основном чертеже являются окружность g экватора относительно Ï1 и уже упомянутая окружность m главного меридиана относительно Ï2.
На рис. 7.26 - 7.28 показано построение произвольной точки M, принадлежащей соответствующей поверхности Ô, для чего использовались проекции q1 и q2 произвольной окружности q Ô.
Ô.

|
|
69 |
|
|
|
q 2 |
|
q 2 |
|
m2 |
12 |
m2 |
1 |
2 |
|
M2 |
|
M2 |
|
|
j2 |
g2 |
j2 |
|
|
|
|
|
m1 |
M1 |
g1 |
|
M1 |
|
11 |
1 |
||
|
|
|
|
|
||
m1 |
j1 |
C m1 |
q1 |
|
j1 C m1 |
q1 |
|
|
|
|
|
||
|
Рис. 7.27 |
|
|
Рис. 7.28 |
|
|
|
|
|
7.3. Винтовые поверхности |
|
|
|
В курсе рассматривают только линейчатые винтовые |
||||||
поверхности - геликоиды, формула которых имеет вид: |
|
|||||
Ô {t(k,j, |
)(ti |
k, ti j, ti |
j = )}, где t - образующая, прямая ли- |
|||
ния; k - цилиндрическая винтовая линия; j - прямая, ось винтовой линии; - постоянный угол наклона образующей ti к оси j.
- постоянный угол наклона образующей ti к оси j.
Если  = 90
= 90 , то геликоид называется прямым, если
, то геликоид называется прямым, если  = 90
= 90 , то наклонным (косым). Формулу прямого геликоида можно записать так: Ô {t(k,j)(ti
, то наклонным (косым). Формулу прямого геликоида можно записать так: Ô {t(k,j)(ti k, ti
k, ti j, ti
j, ti  j)}. Если при вращении точки вокруг оси по часовой стрелке, точка удаляется от наблюдателя, то винтовая линия и геликоид являются правыми, а если приближается, то левыми.
j)}. Если при вращении точки вокруг оси по часовой стрелке, точка удаляется от наблюдателя, то винтовая линия и геликоид являются правыми, а если приближается, то левыми.
На рис. 7.29 приведен элементарный чертеж прямого геликоида, а на рис. 7.30 - наклонного. На чертежах для наглядности построены проекции нескольких образующих, а также заданы направление вращения и проекции точки A, определяющие направление винтовой линии (на рис. 7.29 линия правая, на рис. 7.30 - левая).
Для построения образующих наклонного геликоида принимают, что любая его образующая ti параллельна соответ-
ствующей образующей li |
вспомогательной конической поверхнос- |
ти вращения { l (l, j; l |
j)(l = li j)}, у которой все образующие |

70
t22 |
|
|
|
|
A2 |
1 |
|
|
|
j2 |
|
|
|
|
t2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
j2 |
|
|
|
k2 |
|
|
|
k2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ti |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
22 |
|
t1 |
|
|
l |
|
t2 |
|
l2i |
|
2 |
|
|
2 |
|
2 |
|
|
|
A2 |
|
|
|
|
|
|
|
|
|
|
k1 |
|
|
|
|
12 |
|
|
|
|
|
|
|
11 21 |
|
|
|
|
|
|
|
|
|
ti |
li |
|
|
|
|
|
|
|
1 |
1 |
A |
j1 |
|
1 |
2 |
A 1 |
j |
1 |
|
1 |
|
l1 |
t1 t1 |
|
|
|||
|
|
|
|
|
|
|||
t11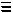 t21
t21
k 1
Рис. 7.29 |
Рис. 7.30 |
наклонены к оси вращения под тем же углом  . Поскольку геликоид и коническая поверхность имеют общую ось j, перпендикулярную Ï1, то горизонтальные проекции образующих поверхностей совпадают: t1i
. Поскольку геликоид и коническая поверхность имеют общую ось j, перпендикулярную Ï1, то горизонтальные проекции образующих поверхностей совпадают: t1i l1i. Задав проекции t1i
l1i. Задав проекции t1i  l1i , строят проекцию l2i образующей конической поверхности, проходящей через её точку 1 и
l1i , строят проекцию l2i образующей конической поверхности, проходящей через её точку 1 и
вершину, а затем через проекцию 22 точки 2 винтовой линии k проводят t2i 
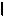 l2i .
l2i .
Винтовые поверхности широко используются в технике: винты, сверла, пружины, конструкции винтовых аппарелей и лестниц и многое другое изготовлено с использованием этих поверхностей.
