начерт

31

уровня. Если плоскость перпендикулярна Ï1, то перпендикуляр к ней является горизонталью h (на рис. 4.3 плоскость Ï1 h11), а если плоскость перпендикулярна Ï2, то фронталью f.

При решении задачи на перпендикулярность двух плоскостей дополнительно используют признак их перпендикулярности: две плоскости взаимно перпендикулярны, если одна из них проходит

проведены l1 h1 l2 f2 ).

равна A,B, строится прямоугольный треугольник A2B2F, катет [B2,F] которого есть разность Y координат Y точек A и B. Откладывая Y от точки K по линии связи (B2,B1), получают два решения B1 и B11.

4.4. Главные позиционные задачи для прямой и плоскости

4.4.1. Общие замечания

К позиционным задачам относятся задачи на принадлежность (принадлежность одних ГО другим - принадлежность точки линии, точки и линии поверхности и т. д.), на взаимное пересечение (пересечение линии и линии, линии и поверхности, поверхности и поверхности) и на взаимный порядок (на размещение ГО в пространстве и расположение одних ГО относительно других).

Главное содержание раздела позиционных задач составляют задачи на взаимное пересечение, называемые поэтому главными позиционными задачами (ГПЗ). Различают 1ГПЗ - задачу на пересечение линии и поверхности и 2ГПЗ - задачу на пересечение поверхностей (задача на пересечение линии и линии имеет очевидное решение, опирающееся на свойство операции проецирования).

Решение ГПЗ осуществляется согласно трем алгоритмам, соответствующим трем возможным случаям расположения пересекающихся ГО относительно плоскостей проекций. Но во всех случаях в основе решения ГПЗ - задача на принадлежность точек поверхности (ОПЗ) и условие: точка пересечения и линия пересечения одновременно принадлежат каждому из пересекающихся ГО.

4.4.2. Первый случай ГПЗ (ГПЗ-1)

В первом случае ГПЗ пересекаются два проецирующих ГО. Алгоритм решения ГПЗ-1:

1.Обе проекции точки или линии пересечения заданы на КЧ.

2.Они принадлежат основным проекциям пересекающихся ГО.

3.Решение сводится к простановке обозначений.

35

собирательное свойство основной проекции проецирующих ГО и действительно сводится к простановке обозначений.

Пояснения к решению: l là l11 Ã1 lÏ1 l2 x.

4.4.3. Второй случай ГПЗ (ГПЗ-2)

Во втором случае ГПЗ один пересекающийся ГО проецирующий, а второй непроецирующий. Алгоритм решения ГПЗ-2:

1.Одна проекция точки или линии пересечения задана на КЧ.

2.Она принадлежит основной проекции проецирующего ГО и её надо только обозначить.

3.Неизвестная проекция точки или линии пересечения ищется из условия принадлежности точки или линии непроецирующему ГО.

Во втором случае ГПЗ необходимо определять видимость

сительно Ï1 , а вторая нет. Для определения видимости прямой

точка 2 и вся часть прямой, на которой она находится, видна относительно Ï1 .

36

дальше от Ï2, чем точка 1 прямой, поэтому точка 1 и часть прямой a, на которой она находится, относительно Ï2 не видны.

относительно Ï1 (границей видимости является прямая l) исполь-

в проецирующее положение. В результате вместо 1ГПЗ-3 в системе ПП ( Ï1, Ï3) решалась 1ГПЗ-2. Проекция 3 плоскости построена с помощью точек A и B, а проекция d3 прямой - c помощью точек 1 и 2.

4.4.5. Третий случай 2ГПЗ(2ГПЗ-3) для плоскостей

В этом случае пересекаются непроецирующие плоскости и обе проекции линии их пересечения неизвестны. 2ГПЗ для плоскостей общего положения решается методом вспомогательных проецирующих плоскостей, основанным на том, что линии пересечения данных плоскостей со вспомогательной пересекаются в точке, лежащей на линии пересечения данных плоскостей. Поэтому алгоритм решения 2ГПЗ-3 для плоскостей формулируется так:

1.Задается вспомогательная проецирующая плоскость, пересекающая данные плоскости.

2.Строятся линии пересечения вспомогательной плоскости с каждой из данных.

3.Определяется точка пересечения построенных в пункте 2

прямых.

4.Задается вторая вспомогательная плоскость и повторяются построения по пунктам 2,3.

5.Искомая линия пересечения проходит через две построенные точки.

ПРИМЕР: 4.10. Дано: Ã(A,B,D,A), (a b) (рис. 4.21). l Ã.

При решении примера использовали вспомогательные плоскости и 1, параллельные Ï1 и пересекающие плоскости Ã и

по горизонталям. Построения выполнялись согласно ПА:

40

позиционных задач или с преобразованием КЧ с использованием четырех ОЗПЧ и свойств прямых и плоскостей частного положения.

5.2. Определение расстояния от точки до плоскости

Расстояние от точки M до плоскости 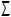равно длине отрезка 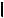M,K перпендикуляра l, опущенного из точки на плоскость (рис. 5.1). Задача решается согласно ПА (не зависит от способа решения):

1.Через точку M проводят перпендикуляр l к плоскости -1ОМЗ.

2.Ищут точку K пересечения перпендикуляра l с плоскостью - 1ГПЗ.

3. Определяют длину отрезка M,K перпендикуляра l - 2ОМЗ.

Рассматриваемая задача является ключевой для группы задач, в которую, в частности, входят задачи: определить расстояние между прямой и параллельной ей плоскостью; определить расстояние между параллельными плоскостями; через точку плоскости провести к плоскости отрезок перпендикуляра заданной длины; построить плоскость, параллельную данной плоскости и удаленную от неё на указанное расстояние.

Расстояние от прямой a до параллельной ей плоскости определяется длиной отрезка M,K перпендикуляра l, опущенного из произвольной точки M прямой на плоскость (рис. 5.2). Поэтому, чтобы найти расстояние от прямой до параллельной ей плоскости, достаточно на прямой взять точку и найти расстояние от неё до плоскости, то есть решить ключевую задачу. Расстояние между параллельными плоскостями Ã и измеряется длиной отрезка M,K перпендикуляра l, опущенного из произвольной точки M одной плоскости на другую (рис. 5.3). Следовательно, чтобы найти расстояние между параллельными плоскостями, достаточно в одной из плоскостей взять точку и найти расстояние от неё до второй плоскости, то есть опять же решить ключевую задачу.