начерт

91

Горизонтальные проекции линий пересечения конической поверхности и секущих плоскостей строят по их известным фронтальным проекциям и условию принадлежности линий пересечения поверхности конуса. Для этого обычно используют окружности q i , проецирующиеся на Ï2 и Ï3 в отрезки прямых, а на Ï1 - в окружности. Ниже дан ГА построения горизонтальных проекций точек M и P гиперболы по их произвольно взятой фронтальной проекцииM2 P2:

Проекции M3 и P3 найдены с использованием их координат YM и YÐ, взятых в поле Ï1 и откладываемых в нужные стороны от оси z3 по линии связи (M2,M3).

Аналогично строили проекции точек Q, G, B, C, F, K, D, E и не указанных промежуточных точек эллипса и гиперболы. Точки B, C, D,

Относительно Ï3 всегда видны точки конической поверхности, расположенные перед контурными образующими l3 и l4 и проецирующиеся на Ï2 и Ï1 левее соответствующих проекций этих образующих. Поэтому относительно Ï3 видны точки гиперболы, дуга эллипса NGAQS и части дуг окружностей от точек F и K до образующих l3 и l4. Из-за сквозного выреза в конусе на Ï3 видны также части

отрезков [C,E] и [B,D].

Отрезки, по которым пересекаются секущие плоскости, находятся внутри конуса и поэтому относительно Ï1 и Ï3 не видны (отрезок [F,K]=ÃÔ конкурирует на Ï1 с гиперболой).

Контурные относительно Ï3 образующие l3 и l4 вырезаны от точек N и S до плоскости Ô и показаны на этих участках тонкими линиями как не существующие.

92

ПРИМЕР 10.3. Задан вид шара со сквозным вырезом на Ï2 (см. вид шара на Ï2 на рис. 10.5 без обозначений). Построить изображения шара на Ï1 и Ï3 (рис. 10.5).

Изображением шара на Ï2 является проекция m2 его главного меридиана m, на Ï1 - проекция q1 его экватора q, на Ï3 - проекция g3 его профильного меридиана g. На рис. 10.5 также даны проекции координатных осей и начала отсчета O.

(поверхности шара) с секущими поверхностями и секущих поверхностей между собой известны - они совпадают с основными проекциями проецирующих поверхностей на Ï2 (на рис. 10.5 обозначены k2 ). Поэтому решение задачи сводится к построению горизонтальных и профильных проекций указанных линий пересечения по их известным фронтальным проекциям.

93

Плоскость пересекает сферу по окружности, проецирующей- ся на Ï2 в отрезок [A2,F2], а на Ï1 и Ï3 - в эллипсы, не существующая дуга EFC которых показывается на чертеже тонкой линией. Плоскость Ã пересекает сферу по полуокружности g1 , проецирующейся на Ï2 в отрезок [K2,L2 ] длиной, равной радиусу этой окружности, на Ï1 - в отрезок [K1 ,N1 ], на Ï3 - в полуокружность g13.

Общая ось вращения сферы и цилиндрической поверхности Ô перпендикулярна Ï2. Поэтому сфера и поверхность Ô соосны и пересекаются по двум полуокружностям m1 и m2, проходящим через точки C,K и E,N соответственно. На Ï2 эти полуокружности проецируются в полуокружность Ô2, а на Ï1 и Ï3 - в отрезки прямых.

Характерные точки A и F расположены на главном меридиане сферы m, а C, E, K и N на её экваторе q.

Горизонтальные проекции промежуточных точек 1 и 2 для по-

Профильные проекции этих точек построены по их фронтальным и горизонтальным проекциям с использованием координаты Y. Аналогично определены проекции характерных точек B и D, задающих положение второй оси эллипсов и других их произвольных точек (при необходимости).

Ï1 , ни на Ï3. На Ï3 показана проекция t3 нижней контурной образующей t цилиндрической поверхности Ô.

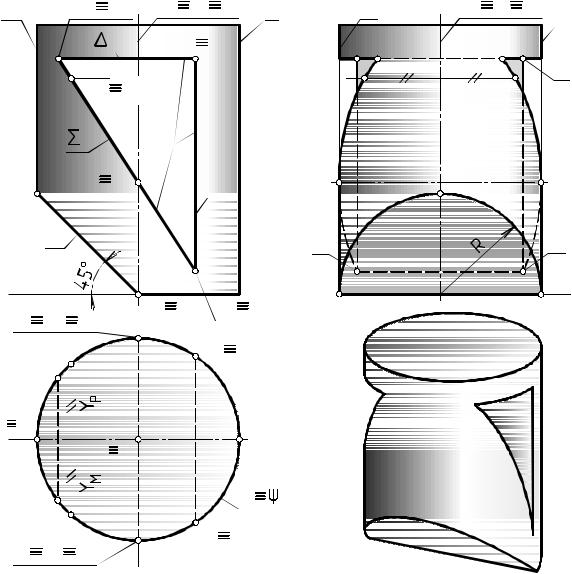
ПРИМЕР 10.4. Задан вид цилиндра вращения на Ï2 и основные проекции фронтально проецирующих плоскостей, образующих в цилиндре сквозной вырез (см. вид цилиндра на Ï2 на рис. 10.6 без обозначений). Построить виды цилиндра с вырезом на ПП Ï1 и Ï3

(рис. 10.6).

Цилиндр ограничен цилиндрической поверхностью вращения и плоскостями верхнего и нижнего оснований.

94

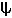
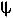
Особенность задачи: секущие плоскости являются проецирующими на Ï2 , а цилиндрическая поверхность на Ï1 . Поэтому известны две проекции линий пересечения k секущих плоскостей и цилиндрической поверхности: на Ï1 эти линии проецируются в окружность 1 - основную проекцию поверхности цилиндра (k11) , а на Ï2 - в ломаную k2, образованную основными проекциями секущих плоскостей. Поэтому в примере строили профильные проекции указанных линий пересечения по их известным горизонтальным и фронтальным проекциям.

На рис. 10.6 помимо изображений цилиндра с вырезом обозначены секущие плоскости, проекции контурных образующих цилиндра, проекции координатных осей связанной с ним системы координат, выделены и обозначены характерные и некоторые промежуточные точки линий пересечения.

95

Плоскость пересекает цилиндрическую поверхность по дугам эллипса ATC и BSD, которые на Ï2 проецируются в отрезок [A2 ,C2], на Ï1 - в дуги A1C1 и B1 D1 окружности 1, а на Ï3- в дуги эллипса B3S3 D3 и A3 T3 C3 , которые построены по точкам. Рассмотрим порядок построения профильных проекций точек на примере построения произвольных точек эллипса M и P:

-на 2 взяли произвольную фронтальную проекцию M2P2 конкурирующих точек M и P;

-на 1 с помощью вертикальной линии связи, проведенной из точки M2 P2, найдены проекции M1 и P1 (точка M видна относитель-

Плоскость Ô пересекает цилиндрическую поверхность по дуге эллипса LKN, который на Ï2 проецируется в отрезок [K2,L2], на Ï1 -

Плоскость перпендикулярна оси цилиндра и пересекает его поверхность по дугам AE и BF окружности, которые на Ï2 и Ï3 проецируются в отрезки прямых, а на Ï1 - в дуги окружности. Плоскость Ã параллельна оси цилиндра и пересекает его поверхность по

Кроме того, из-за выреза части геометрического тела могут быть видны точки, расположенные за образующими l3 и l4 , например,

96

точки E и F. Поэтому части отрезков [E,C] и [F,D], расположенные в “задней” относительно Ï3 половине цилиндра, “выглядывают” из-за дуг эллипса и становятся видимыми.

Отрезки, по которым пересекаются секущие плоскости, расположены внутри цилиндра и относительно Ï3 не видны.

10.3. Построение натурального вида плоской фигуры, получаемой при пересечении геометрического тела плоскостью

Такие задачи имеют практическое значение, так как при выполнении производственных чертежей иногда возникает необходимость определить натуральный вид фигуры сечения, получаемой при рассечении изделия плоскостью, не параллельной ПП.

Рис. 10.7

На рис. 10.7 строится натуральный вид сечения сложного геометрического тела,ограниченного горизонтальнопроецирующими цилиндрическими Ô и ипризматической 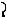поверхностями, горизонтальными плоскостями , 1 и 2 и плоскостью Ï2 . Задача свелась к решению 4ОЗПЧ и заданию новой ПП Ï3 Ï3Ï2. В

97

качестве оси x12 задавалась ось симметрии фигуры на Ï1 . При построении натурального вида сечения симметричные точки не обоз-

начались. Расстояние, используемое для получения проекции 13 , на рис. 10.7 отмечено фигурной скобкой. Точка 9 - промежуточная для построенияэллипса.

СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ

1.Локтев О.В. Краткий курс начертательной геометрии: Учеб. для втузов.-3-е изд., испр.-М.: Высш.шк., 1999.-136с.

2.Кузнецов Н.С. Начертательная геометрия: Учеб. для втузов.-2-е изд., перераб. и доп.-М.: Высш.шк., 1981.-262с.

3.Нартова Л.Г. Начертательная геометрия: Учеб. для вузов / Л.Г. Нартова, В.И.Якунин.-М.: Дрофа, 2003.-208с.

4.Фролов С.А. Начертательная геометрия: Учеб. для втузов.-2-е изд., перераб. и доп.-М.: Машиностроение., 1983.-240с.

5.Оганесов О.А. Курс лекций по начертательной геометрии: Учебное пособие для студентов механических специальностей /

МАДИ(ГТУ). Часть 1. -М., 2002.-101с.

6.Оганесов О.А. Курс лекций по начертательной геометрии: Учебное пособие для студентов механических специальностей /

МАДИ(ГТУ). Часть 2. -М., 2002.-79с.

7.Оганесов О.А., Кузенева Н.Н. Пересечение поверхностей. Методическое пособие к выполнению расчетно-графической работы для студентов механических специальностей

/ МАДИ(ГТУ). -М., 2002. -79с.

8.Оганесов О.А., Кузенева Н.Н. Инженерная графика. Справочные материалы: Учебное пособие / МАДИ(ГТУ). Часть 1. -М., 2006. -94с.

Олег Авакович ОГАНЕСОВ, Виктор Александрович КАЙЛЬ,

Ирина Михайловна РЯБИКОВА, Наталья Николаевна КУЗЕНЕВА

КУРС ЛЕКЦИЙ ПО НАЧЕРТАТЕЛЬНОЙ ГЕОМЕТРИИ

Учебное пособие для студентов строительных специальностей

Часть 1

Редактор Ю.К.Фетисова

Ротапринт МАДИ(ГТУ). 125319, Москва, Ленинградский проспект, 64