УЧЕБНОЕ ПОСОБИЕ ПРОЕКТИРОВАНИЕ АД

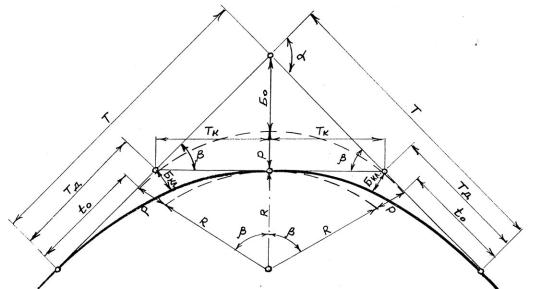
Рис. 2.8. Расчетная схема закругления из симметричной биклотоиды (без круговой вставки)

Подбирая радиусы биклотоид, необходимо руководствоваться фактическим расстоянием между вершинами смежных углов помня, что на данном участке длиной Sn должны разместиться тангенсы двух смежных биклотоид, т.е. должно быть выдержано условие Sn Т Бn Т Бn 1 . Кроме того, сложная математическая зависимость

между радиусами смежных кривых R1 и R2 и длинами переходных кривых L1 и L2 затрудняет практические расчеты клотоидной трассы. Поэтому для вычисления элементов сопряжений клотоидных кривых используются специальные таблицы для клотоидного проектирования

[13].

2.3.1. ПРИМЕР ПРОЕКТИРОВАНИЯ БИКЛОТОИДНЫХ ЗАКРУГЛЕНИЙ

Задание: запроектировать южный вариант трассы (см. рис. 2.1) с закруглениями из симметричных биклотоид большого параметра А.

Исходные данные принять согласно рис. 2.2.

Решение

Проектирование биклотоидных закруглений южного варианта трассы выполняем в такой последовательности.

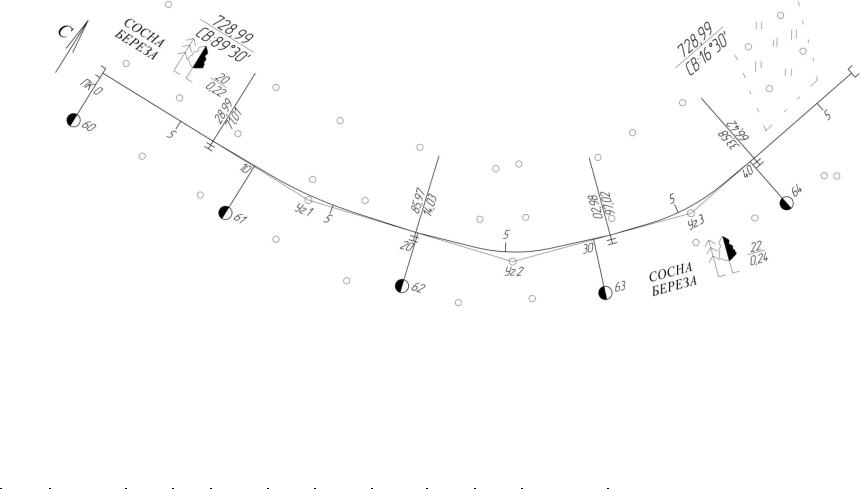
1. Устанавливаем по таблице на рис. 2.2 расчетные данные: Угол № 1 (ПК13+60), α1=15°00´.

Угол № 2 (ПК25+56,24), α2=32°00´ .

51

Угол № 3 (ПК35+66,74), α3=26°00´.

Расстояния между вершинами: S1=1360 м, S2=1200 м, S3=1040

м, S4=1200 м.

2. Подбором назначаем радиусы клотоид (в точке их стыкования), ориентируясь на фактические расстояния между смежными углами поворота трассы S1, S2, S3, S4 и значения углов α1, α2, α3 (см. рис.

2.2).

Определение (подбор) радиусов начинаем с закругления №2, как наиболее сложного для укладки клотоид (наименьшие расстояния между вершинами смежных углов).

Значение радиуса R2 назначаем путем следующего логического рассуждения: при укладке биклотоиды на закруглении №2 необходи-

разместиться по одной ветви второй и третьей биклотоид), а поскольку элементы смежных закруглений предпочтительно назначать одинаковыми, то ориентировочно принимаем тангенсы биклотоид №2 и №3 равными половине расстояния между углами: TБ1 TБ2 S3 2 .

Следовательно, TБ2 10402 . По аргументу α2=32° находим по табл.

Iа Ксенодохова [13] значение тангенса симметричной биклотоиды для R=100 м и вычисляем отношение тангенсов принятого TБ2 к таблич-

ному Ттабл:

К ТБ2 Ттабл 52056,899 9,139 .

Для упрощения вычислений принимаем К=10 и вычисляем окончательное значение радиуса биклотоиды путем умножения табличного значения Tтабл 100 м на отношение TБ2 Tтабл 10 .

R2=100·10=1000 м.

Находим фактический тангенс биклотоиды при R2 = 1000 м:

TБ2 56,899 10 568,99 м

3. Определяем радиус симметричной биклотоиды №3. Для этого предварительно вычисляем длину участка, оставшегося после укладки тангенса второй биклотоиды, т.е. вычисляем разность

S3 TБ2 1040 568,99 474,01 м.

На оставшемся расстоянии S3 TБ2 необходимо разместить тан-

генс биклотоиды № 3, причем без остатка. Поэтому принимаем TБ3 471,01 м и находим табличное значение тангенса по аргументу

α=26° 00´; Ттабл. =45,935 м, вычисляем отношение тангенсов

52

лотоид, последовательно, начиная с Уг1, вычисляем фактические параметры биклотоид, умножая табличные значения на отношение

Rфакт Rтабл .

Биклотоида №1 (α=15°00´; R=2400,65 м).

Отношение радиусов ТфактТтабл 2400,65100 24,0065 . Фактические значения элементов биклотоиды:

тангенс биклотоиды TБ1 26,285 24,0065 631,01 м; длина биклотоиды KБ1 56,360 24,0065 1353,06 м; домер биклотоиды Д Б1 0,211 24,0065 5,06 м;

параметр биклотоиды А 51,166 24,0065 1228,32 ;

длина ветви биклотоиды LБ1 26,180 24,0065 628,49 м. Биклотоида №2 (α=32°00´; R=1000 м)

Отношение радиусов Rфакт Rтабл 1000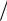100 10 . Фактические значения элементов биклотоиды:

тангенс биклотоиды TБ2 65,899 10 568,99 м ;

длина биклотоиды KБ2 111,701 10 1117 ,01 м;

биссектриса биклотоиды ББ2 5,378 10 53,78 м; домер биклотоиды Д Б2 2,097 10 20,97 м ; параметр биклотоиды АБ2 55,851 10 558,51; длина ветви биклотоиды LБ2 55,851 10 558,51 м.

Биклотоида №3 (α=26° 00´ ; R=1025,38 м) 53

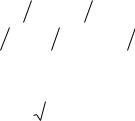
Отношение радиусов Rфакт Rтабл 1025,38100 10,2538 .

Фактические значения элементов биклотоиды: тангенс биклотоиды TБ3 45,935 10,2538 471,01 м;

длина биклотоиды K Б3 90,757 10,2538 930,60 м;

биссектриса биклотоиды ББ3 3,509 10,2538 35,98 м;

домер биклотоиды Д Б3 1,113 10,2538 11,42 м; параметр биклотоиды АБ3 67,364 10,2538 690,74 ;

длина ветви биклотоиды LБ3 45,379 10,2538 465,30 м.

6. Вычисляем пикетажное положение вершин углов и основных точек симметричных биклотоид по схеме табл. 2.6 и обозначаем их на плане рис. 2.9.

2.3.2.ДЕТАЛЬНАЯ РАЗБИВКА КЛОТОИДНОЙ ТРАССЫ

Впрактике проектирования дорог наиболее распространенным методом детальной разбивки клотоид является метод ординат и абсцисс от главной касательной. Главной касательной называют точку отхода от начальной прямой, где ρ=∞ (рис. 2.10).

Суть данного метода заключается в том, что координаты клотоиды x и y вычисляют в зависимости от аргумента

l Sn 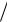А,

где Sn – расстояние от главной касательной клотоиды до точки Мn на ней (текущая длина переходной кривой), м.

Координаты клотоиды, имеющей параметр А=1, можно вычислить по формулам

При A≠1 координаты x и y, вычисленные по формулам (2.18) и (2.19), необходимо умножить на фактическое значение параметра А:

В практике проектирования координаты клотоиды определяют по специальным таблицам для детальной разбивки клотоиды [10].

Задание: выполнить детальную разбивку симметричной биклотоиды, запроектированной на закруглении №2 южного варианта трассы.

Исходные данные принять согласно рис. 2.9 и расчетам, выполненным в п.2.3.

54

0

55

56

Рис. 2.9. План трассы с закруглениями из переходных симметричных биклотоид (южный вариант)

56

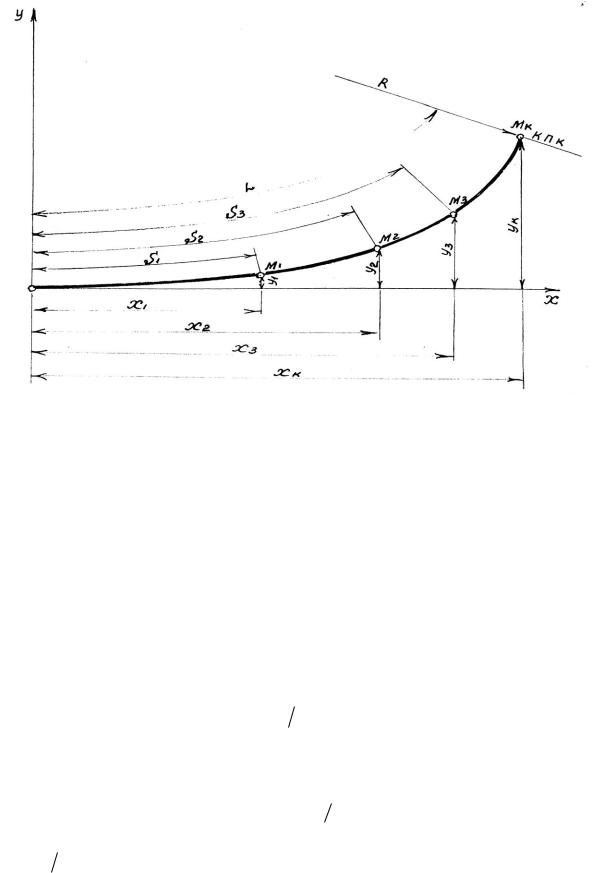
Рис. 2.10. Схема для детальной разбивки клотоиды

Решение

1. По рис. 2.9 устанавливаем условия, необходимые для детальной разбивки клотоиды: ВУ2 ПК25+54,96; α=32°00´.

Начало закругления (положение главной касательной клотоиды)

ПК19+85,97.

Конец закругления ПК31+02,98; радиус биклотоиды R=1000 м;

длина одной ветви симметричной биклотоиды LБ2 558,51 м;

параметр клотоиды А=747,33.

2. Принимаем шаг разбивки клотоиды 25 м (расстояние между промежуточными точками на клотоиде) и вычисляем отношение

где Sn – текущая длина клотоиды (переходной кривой), под которой понимается расстояние от начала клотоиды до промежуточной точки.

Для конечной точки биклотоиды lk 558,51747,33 0,7473 .

3. По аргументу l n выписываем из табл. II [13] координаты хт и ут (при А=100) и вычисляем фактические значения координат клотоиды умножением табличных величин на отношение Аф Атабл .

Например, для l1=0,0334 табличные значения координат хт=3,340 и ут=0,001. Следовательно, фактические координаты клотоиды равны

хф хтабл Аф Атабл , хф 3,34 747,33100 24,96 ; yф 0,001 747,33100 0,01.

Координаты прочих промежуточных точек, вычисленные для одной ветви биклотоиды, представлены в табл. 2.7. Вторая ветвь биклотоиды (вторая половина закругления) разбивается по тем же координатам (зеркальное отражение первой ветви).

Таблица 2.7 Ведомость детальной разбивки клотоиды второго закругления(уг. №2,

южный вариант)

58

2.3.3.ДЕТАЛЬНАЯ РАЗБИВКА КЛОТОИДЫ

ИСОПРЯЖЕННОЙ С НЕЙ КРУГОВОЙ КРИВОЙ

Детальную разбивку клотоиды (переходной кривой), непосредственно сопряженной с круговой кривой (рис. 2.11), как правило, выполняют методом прямоугольных координат X0Y с расположением центра координат в начале клотоиды и с направлением оси абсцисс по начальной (главной) касательной.

Для вычисления координат в системе X0Y используют формулы:

Угол клотоиды β и центральный угол γ в формулах (2.22) и

где К – расстояние от начала клотоиды до точки М, расположенной на круговой части закругления, м (см. рис. 2.11).

Рис. 2.11. Схема детальной разбивки закругления из круговой и переходной кривых

59

Для закругления №2: β=120/2·1500=0,04 рад, или β=2º18´; γ=α– 2β. При α=15º центральный угол γ=15–2·2º18´=10º24, или γ=0,18 рад.

Вычисление координат x и y по формулам трудоемко, поэтому на практике детальную разбивку клотоиды и сопряженной с ней круговой кривой выполняют по таблицам. При известных значениях радиусов круговых кривых R и длин переходных кривых L наиболее удобно пользоваться табл. III [13], где для каждого стандартного (круглого) значения R дан ряд значений длины клотоиды L. Для промежуточных значений R и L табличные значения координат x и y определяют интерполяцией. Для каждого случая R и L в табл. III приведены также некоторые основные элементы клотоиды: А, β, Тд, Тк, t и р, которые могут быть полезны при разбивке трассы.

Задание: определить координаты x и y для разбивки закругления, состоящего из клотоиды и сопряженной с ней круговой кривой.

Исходные данные принять согласно рис. 2.7 (вариант трассы северный, закругления №2 и №3).

Решение

1. Устанавливаем расчетные данные для разбивки закругления №2 северного варианта трассы (см. рис. 2.7):

α2=15°00´, R2=1500 м; L=120 м.

Пикетажное положение основных точек закругления выписываем из табл.2.5.

Начало переходной кривой (начало закругления ) ПК22+14,93. Конец переходной кривой (начало КК) ПК 23+34,93.

Середина закругления (середина круговой кривой) ПК24+71,22.

2.Принимаем шаг разбивки закругления 15 м и определяем по табл. III Ксенодохова значения x и y до середины закругления. Вторая половина закругления разбивается по тем же координатам (зеркально).

3.Расчетные данные для разбивки закругления №3 α=25°00´,

R3=1000 м; L=120 м.

Начало переходной кривой (НПК) ПК30+98,10. Конец переходной кривой (начало КК) ПК32+18,10. Середина закругления (Ср.з.) ПК33+81,15.

Вычисленные по таблицам значения координат x и y для закруглений №2 и №3 северного варианта трассы представлены в табл. 2.8.

60