
Добавил:
Upload
Опубликованный материал нарушает ваши авторские права? Сообщите нам.
Вуз:
Предмет:
Файл:Matematika_3_semestr.docx
X
- •1)Дифференциальные уравнения: основные определения и примеры решения прикладных задач.
- •2)Теорема существования и единственности решения дифференциального уравнения первого и второго порядков.
- •3)Численные методы интегрирования дифференциальных уравнений: метод Эйлера и метод Рунге-Кутта.
- •5)Однородные уравнения.
- •11)Однородные линейные дифференциальные уравнения второго порядка с постоянными коэффициентами.
- •12)Неоднородные линейные дифференциальные уравнения второго порядка. Теорема о структуре общего решения неоднородного линейного дифференциального уравнения второго порядка.
- •13)Метод Лагранжа вариации постоянных.
- •14)Метод неопределенных коэффициентов.
- •15)Линейные колебательные системы. Теорема о суперпозиции.
- •16)Системы линейных дифференциальных уравнений. Однородная линейная система с постоянной матрицей и неоднородная линейная система.
- •17)Числовой ряд. Сумма ряда. Необходимый признак сходимости ряда. Свойства сходящихся рядов.
- •18)Достаточные признаки сходимости знакоположительных числовых рядов: признак сравнения (две формы), признак Даламбера, радикальный признак Коши, интегральный признак Коши.
- •19)Достаточный признак сходимости знакопеременных числовых рядов.
- •20)Достаточный признак сходимости знакочаредующихся числовых рядов (признак Лейбница).
- •21)Функциональный ряд, область сходимости. Свойства правильно сходящихся функциональных рядов.
- •22)Степенной ряд. Свойства степенных рядов. Теорема Абеля. Радиус и интервал сходимости.
- •23)Разложение функции в степенной ряд (ряд Тейлора). Необходимые и достаточные условия разложимости функции в ряд Тейлора.
- •24)Разложение функций…
- •25)Применение степенных рядов к приближенным вычислениям.
- •26)Разложение функции в ряд Фурье. Достаточные условия разложимости функции в ряд Фурье.
- •27)Разложение четных и нечетных функций в ряд Фурье.
27)Разложение четных и нечетных функций в ряд Фурье.
Отметим следующие свойства четных и нечетных функций:
1) 
2) Произведение двух четных и нечетных функций является четной функцией.
3) Произведение четной и нечетной функций – нечетная функция.
Справедливость этих свойств может быть легко доказана исходя из определения четности и нечетности функций. Если f(x) – четная периодическая функция с периодом 2, удовлетворяющая условиям разложимости в ряд Фурье, то можно записать:
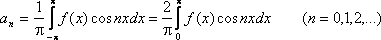
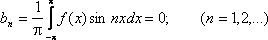
Таким образом, для четной функции ряд Фурье записывается:
![]()

Аналогично получаем разложение в ряд Фурье для нечетной функции:
![]()
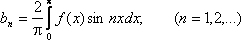
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
