15)Линейные колебательные системы. Теорема о суперпозиции.

Принцип суперпозиции Если правая часть неоднородного уравнения представляет собой сумму нескольких функций вида Pn(x)eαxи/или[Pn(x)cos(βx)+Qm(x)sin(βx)]eαx, то частное решение дифференциального уравнения также будет являться суммой частных решений, построенных отдельно для каждого слагаемого в правой части.

16)Системы линейных дифференциальных уравнений. Однородная линейная система с постоянной матрицей и неоднородная линейная система.

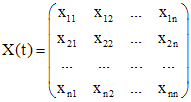Система уравнений вида,  (1)называетсянеоднородной системой линейных дифференциальных уравнений с постоянными коэффициентами. Будем считать, что являются непрерывными функциями на (a,b). Система дифференциальных уравнений, (2) называется однородной. Вводя в рассмотрение векторыи матрицу, уравнения (1),(2) можно представить в векторной форме, (1')(2') Матрица, (3)где- координаты линейно независимых решений (векторов)...........................векторного уравнения (2'), называетсяфундаментальной матрицейэтого уравнения. Иногда ее называютматрицей Вронского.Определитель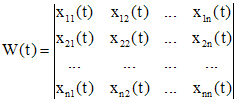, составленный из частных решений системы (2), называетсяопределителем Вронского. Для того, чтобы матрица (3), где- частные решения системы уравнений (2), была фундаментальной, необходимо и достаточно, чтобыпри. При этом общее решение векторного уравнения (2') представляется в виде, гдеC- произвольный постоянный вектор. Общее же решение уравнения (1') будет, где- какой-нибудь вектор, являющийся частным решением уравнения (1'). Путем исключения неизвестных систему всегда можно свести к уравнению более высокого порядка с одной неизвестной функцией. Этот метод удобен для решений несложных систем.

17)Числовой ряд. Сумма ряда. Необходимый признак сходимости ряда. Свойства сходящихся рядов.

Числовой ряд – это сумма членов числовой последовательности вида .Суммой сходящегося числового ряданазывается предел последовательности его частичных сумм, то есть, Числовой рядназывается сходящимся, если существует конечный предел последовательности частичных сумм. Если предел последовательности частичных сумм числового ряда не существует или бесконечен, то рядназывается расходящимся. Если сходится числовой ряд, то сходящимся будет и ряд. Другими словами, сходящимся будет и ряд без первыхmчленов. Если к сходящемуся числовому рядудобавить несколько членов (от первого доm-ого), то полученный ряд также будет сходящимся.

1)Если сходится числовой ряд , то сходящимся будет и ряд. Другими словами, сходящимся будет и ряд без первыхm членов. Если к сходящемуся числовому ряду добавить несколько членов (от первого доm-ого), то полученный ряд также будет сходящимся.

2)Если сходится числовой ряд и его сумма равнаS, то сходящимся будет и ряд , причем, гдеA – произвольная постоянная.

3)Если сходятся числовые ряды и, их суммы равныA и Bсоответственно, то сходящимися будут ряды и, причем их суммы будут равныA + B и A - B соответственно.

18)Достаточные признаки сходимости знакоположительных числовых рядов: признак сравнения (две формы), признак Даламбера, радикальный признак Коши, интегральный признак Коши.

Необходимое и достаточное условие сходимости знакоположительного числового ряда. Для сходимости знакоположительного числового ряданеобходимо и достаточно, чтобы последовательность его частичных сумм была ограничена. Первый признак сравнения рядов. Пустьи- два знакоположительных числовых ряда и выполняется неравенстводля всехk = 1, 2, 3, ...Тогда из сходимости рядаследует сходимость, а из расходимости рядаследует расходимость. Первый признак сравнения используется очень часто и представляет собой очень мощный инструмент исследования числовых рядов на сходимость. Основную проблему представляет подбор подходящего ряда для сравнения. Ряд для сравнения обычно (но не всегда) выбирается так, что показатель степени егоk-огочлена равен разности показателей степени числителя и знаменателяk-огочлена исследуемого числового ряда. К примеру, пусть, разность показателей степени числителя и знаменателя равна2 – 3 = -1, поэтому, для сравнения выбираем ряд сk-ымчленом, то есть, гармонический ряд.

Второй признак сравнения. Пусть и- знакоположительные числовые ряды. Если, то из сходимости рядаследует сходимость. Если, то из расходимости числового рядаследует расходимость.

Следствие. Если и, то из сходимости одного ряда следует сходимость другого, а из расходимости следует расходимость.

Третий признак сравнения. Пусть и- знакоположительные числовые ряды. Если с некоторого номераNвыполняется условие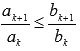, то из сходимости рядаследует сходимость, а из расходимости рядаследует расходимость.

Признак Даламбера. Пусть - знакоположительный числовой ряд. Если, то числовой ряд сходится, если, то ряд расходится.

Замечание. Признак Даламбера справедлив, если предел бесконечен, то есть, если , то ряд сходится, если, то ряд расходится.

Если , то признак Даламбера не дает информацию о сходимости или расходимости ряда и требуется дополнительное исследование.

Радикальный признак Коши. Пусть - знакоположительный числовой ряд. Если, то числовой ряд сходится, если, то ряд расходится.

Замечание. Радикальный признак Коши справедлив, если предел бесконечен, то есть, если , то ряд сходится, если, то ряд расходится. Если, то радикальный признак Коши не дает информацию о сходимости или расходимости ряда и требуется дополнительное исследование.

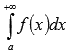Интегральный признак Коши. Пусть - знакоположительный числовой ряд. Составим функцию непрерывного аргументаy = f(x), аналогичную функции. Пусть функцияy = f(x)положительная, непрерывная и убывающая на интервале, где). Тогда в случае сходимостинесобственного интеграласходится исследуемый числовой ряд. Если же несобственный интеграл расходится, то исходный ряд тоже расходится.