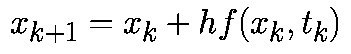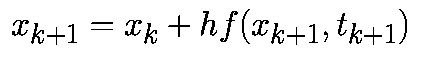- •1)Дифференциальные уравнения: основные определения и примеры решения прикладных задач.
- •2)Теорема существования и единственности решения дифференциального уравнения первого и второго порядков.
- •3)Численные методы интегрирования дифференциальных уравнений: метод Эйлера и метод Рунге-Кутта.
- •5)Однородные уравнения.
- •11)Однородные линейные дифференциальные уравнения второго порядка с постоянными коэффициентами.
- •12)Неоднородные линейные дифференциальные уравнения второго порядка. Теорема о структуре общего решения неоднородного линейного дифференциального уравнения второго порядка.
- •13)Метод Лагранжа вариации постоянных.
- •14)Метод неопределенных коэффициентов.
- •15)Линейные колебательные системы. Теорема о суперпозиции.
- •16)Системы линейных дифференциальных уравнений. Однородная линейная система с постоянной матрицей и неоднородная линейная система.
- •17)Числовой ряд. Сумма ряда. Необходимый признак сходимости ряда. Свойства сходящихся рядов.
- •18)Достаточные признаки сходимости знакоположительных числовых рядов: признак сравнения (две формы), признак Даламбера, радикальный признак Коши, интегральный признак Коши.
- •19)Достаточный признак сходимости знакопеременных числовых рядов.
- •20)Достаточный признак сходимости знакочаредующихся числовых рядов (признак Лейбница).
- •21)Функциональный ряд, область сходимости. Свойства правильно сходящихся функциональных рядов.
- •22)Степенной ряд. Свойства степенных рядов. Теорема Абеля. Радиус и интервал сходимости.
- •23)Разложение функции в степенной ряд (ряд Тейлора). Необходимые и достаточные условия разложимости функции в ряд Тейлора.
- •24)Разложение функций…
- •25)Применение степенных рядов к приближенным вычислениям.
- •26)Разложение функции в ряд Фурье. Достаточные условия разложимости функции в ряд Фурье.
- •27)Разложение четных и нечетных функций в ряд Фурье.
1)Дифференциальные уравнения: основные определения и примеры решения прикладных задач.
Дифференциальное уравнение (ДУ) – это уравнение, в которое входит неизвестная функция под знаком производной или дифференциала. Если неизвестная функция является функцией одной переменной, то дифференциальное уравнение называют обыкновенным (сокращенно ОДУ – обыкновенное дифференциальное уравнение). Если же неизвестная функция есть функция многих переменных, то дифференциальное уравнение называют уравнением в частных производных.Максимальный порядок производной неизвестной функции, входящей в дифференциальное уравнение, называется порядком дифференциального уравнения. Решение дифференциального уравнения - это неявно заданная функция Ф(x, y) = 0 (в некоторых случаях функцию y можно выразить через аргумент x явно), которая обращает дифференциальное уравнение в тождество.
2)Теорема существования и единственности решения дифференциального уравнения первого и второго порядков.
Определение
1.Дифференциальным уравнением
первого порядка называется уравнение,
связывающее независимую переменную![]() ,
искомую функцию
,
искомую функцию![]() и
ее производную первого порядка
и
ее производную первого порядка![]() ,
то есть
,
то есть
![]() .
(1) Если уравнение (1) можно разрешить
относительно
.
(1) Если уравнение (1) можно разрешить
относительно![]() ,
то его записывают в виде
,
то его записывают в виде
![]() .
(2) Обозначим через
.
(2) Обозначим через![]() множество
точек плоскости
множество
точек плоскости![]() ,
на котором функция
,
на котором функция![]() определена.
Рассмотрим геометрический смысл
уравнения (2). Производная функции
определена.
Рассмотрим геометрический смысл
уравнения (2). Производная функции![]() представляет
собой угловой коэффициент (тангенс угла
наклона) касательной к кривой
представляет
собой угловой коэффициент (тангенс угла
наклона) касательной к кривой![]() в
точке с абсциссой
в
точке с абсциссой![]() .
Следовательно, уравнение (2) устанавливает
связь (зависимость) между координатами
каждой точке
.
Следовательно, уравнение (2) устанавливает
связь (зависимость) между координатами
каждой точке![]() плоскости
плоскости![]() и
угловым коэффициентом
и
угловым коэффициентом![]() касательной
к интегральной кривой
касательной
к интегральной кривой![]() ,
проходящей через эту точку. Если указать
это направление единичным вектором,
проходящим через точку
,
проходящей через эту точку. Если указать
это направление единичным вектором,
проходящим через точку![]() ,
то будет получено поле направлений.
,
то будет получено поле направлений.
Определение 2.Кривая, во всех точках которой направление поля одинаково, называетсяизоклиной.
Изоклинами
можно пользоваться для приближенного
построения интегральных кривых. Уравнение
изоклины можно получить, если положить ![]() ,
то есть
,
то есть![]()
3)Численные методы интегрирования дифференциальных уравнений: метод Эйлера и метод Рунге-Кутта.
Прямой метод Эйлера- аппроксимируем производную в момент времени tkсоотношением
 При
такой аппроксимации уравнение (1) примет
вид:
При
такой аппроксимации уравнение (1) примет
вид:
|
|
(2) |
Формула
(2) известна как прямой метод Эйлера.
На рис.1(a) показана графическая
интерпретация прямого метода Эйлера.
На (k+1)-ом шаге векторное поле предполагается
(локально) постоянным со значением
f(xk,tk). Рис.1
Иллюстрация алгоритмов (а) прямого
метода Эйлера, (b) обратного метода
Эйлера. Меньшее значение величины шага
h в итоге дает точки аппроксимации чаще
и, как демонстрирует рис.2, приводит к
большей точности интегрирования, что
приобретает математический смысл,
поскольку (2) стремится к (1) при h->0.
Рис.1
Иллюстрация алгоритмов (а) прямого
метода Эйлера, (b) обратного метода
Эйлера. Меньшее значение величины шага
h в итоге дает точки аппроксимации чаще
и, как демонстрирует рис.2, приводит к
большей точности интегрирования, что
приобретает математический смысл,
поскольку (2) стремится к (1) при h->0. Рис.2
Влияние величины шага. Уравнение
dx/dt=-6x+5t-tинтегрируется от x=1
прямым методом Эйлера при h=0.3 (а) и при
h=0.1 (b). Точное решение показано штриховой
линией.Обратный метод Эйлера-
обратный метод Эйлера подобен прямому,
но есть одно отличие в аппроксимации
для производной
Рис.2
Влияние величины шага. Уравнение
dx/dt=-6x+5t-tинтегрируется от x=1
прямым методом Эйлера при h=0.3 (а) и при
h=0.1 (b). Точное решение показано штриховой
линией.Обратный метод Эйлера-
обратный метод Эйлера подобен прямому,
но есть одно отличие в аппроксимации
для производной
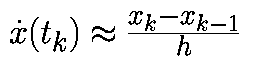 .
Такая аппроксимация дает формулу
обратного метода Эйлера:
.
Такая аппроксимация дает формулу
обратного метода Эйлера:
|
|
(3) |
На рис.1(b)
показана геометрическая интерпретация
обратного метода Эйлера. На (k+1)-ом шаге
векторное поле предполагается (локально)
постоянным со значением f(xk+1,tk+1).
Обратный
метод Эйлера - это примернеявного
алгоритма интегрирования , где
xk+1является функцией от самой
себя. И напротив, прямой метод Эйлера
представляет собойявный алгоритм.
В неявных алгоритмах для определения
xk+1требуются дополнительные
вычисления, но они по сравнению с
аналогичными прямыми алгоритмами более
устойчивы и дают более высокую точность
вычислений (см. рис.3). Возможно это
обусловлено наличием члена xk+1в
правой части формулы, что может
рассматриваться как вид обратной
связи. Рис.3
Та же система, что и на рис.2 проинтегрирована
от x0=1.0 с h=0.3 (a) прямым методом
Эйлера, (b) обратным методом Эйлера.
Точное решение показано штриховой
линией.Метод Рунге-Кутта- в основу
семейства алгоритмов Рунге-Кутта
положена идея аппроксимации фt(xk)
рядом Тейлора. Рассмотрим алгоритмы
второго и четвертого порядков. Термин
"k-го порядка" означает, что в
аппроксимации используется k членов
ряда Тейлора.Метод Рунге-Кутта второго
порядка - имеется целое семейство
уравнений Рунге-Кутта второго порядка.
Мы рассмотрим модифицированный алгоритм
Эйлера-Коши, заданный соотношением:
Рис.3
Та же система, что и на рис.2 проинтегрирована
от x0=1.0 с h=0.3 (a) прямым методом
Эйлера, (b) обратным методом Эйлера.
Точное решение показано штриховой
линией.Метод Рунге-Кутта- в основу
семейства алгоритмов Рунге-Кутта
положена идея аппроксимации фt(xk)
рядом Тейлора. Рассмотрим алгоритмы
второго и четвертого порядков. Термин
"k-го порядка" означает, что в
аппроксимации используется k членов
ряда Тейлора.Метод Рунге-Кутта второго
порядка - имеется целое семейство
уравнений Рунге-Кутта второго порядка.
Мы рассмотрим модифицированный алгоритм
Эйлера-Коши, заданный соотношением:
 Из
этой формулы следует, что модифицированный
алгоритм Эйлера-Коши включает два этапа.
На первом этапе с помощью прямого метода
Эйлера происходит перемещение на пол
шага вперед к моменту времени (tk+h/2):
Из
этой формулы следует, что модифицированный
алгоритм Эйлера-Коши включает два этапа.
На первом этапе с помощью прямого метода
Эйлера происходит перемещение на пол
шага вперед к моменту времени (tk+h/2):
 На
втором этапе это промежуточное значение
используется для аппроксимации векторного
поля с помощью итераций Эйлера прямого
типа:
На
втором этапе это промежуточное значение
используется для аппроксимации векторного
поля с помощью итераций Эйлера прямого
типа:
 Модифицированный
алгоритм Эйлера-Коши использует значение
векторного поля в средней точке между
xkи xk+1. Он отличается от
трапецеидального алгоритма, в котором
используется среднее значение векторного
поля по xkи xk+1. Его можно
рассматривать как явный алгоритм,
который, используя промежуточный шаг
по времени, включен в неявный алгоритм.Метод Рунге-Кутта четвертого порядка- как и в случае алгоритма второго порядка
метод Рунге-Кутта четвертого порядка
относится к явным алгоритмам. Он
использует промежуточные моменты
времени для для вычисления состояния
в момент времени tk+1. Следующие
формулы определяют алгоритм Рунге-Кутта
четвертого порядка:
Модифицированный
алгоритм Эйлера-Коши использует значение
векторного поля в средней точке между
xkи xk+1. Он отличается от
трапецеидального алгоритма, в котором
используется среднее значение векторного
поля по xkи xk+1. Его можно
рассматривать как явный алгоритм,
который, используя промежуточный шаг
по времени, включен в неявный алгоритм.Метод Рунге-Кутта четвертого порядка- как и в случае алгоритма второго порядка
метод Рунге-Кутта четвертого порядка
относится к явным алгоритмам. Он
использует промежуточные моменты
времени для для вычисления состояния
в момент времени tk+1. Следующие
формулы определяют алгоритм Рунге-Кутта
четвертого порядка:
|
|
(4) |
Каждое из четырех Kiявляется аппроксимирующим значением векторного поля. K1- значение векторного поля при xk. K2- аппроксимированное значение на полшага позже, в момент времени tk+h/2. В сущности, это прямой метод Эйлера с временным шагом h/2. K3- также значение векторного поля в момент tk+h/2, но вычисляется с использованием K2. Это схоже с обратным методом Эйлера с половинным шагом, за исключением того, что вместо неявного разложения (3) используется явная аппроксимация для f в момент времени tk+h/2. K4- значение векторного поля в момент tk+1, вычисляется с использованием основного последнего значения K3. Это модифицированный шаг Эйлера-Коши. Наконец, эти четыре значения усредняются, чтобы дать аппроксимацию векторного поля для определения xk+1.
4)Уравнения
с разделенными и разделяющимися
переменными. Дифференциальные
уравнения с разделенными
переменными ![]() .
Дифференциальные
уравнения с разделяющимися
переменными
.
Дифференциальные
уравнения с разделяющимися
переменными ![]() .
Дифференциальные
уравнения, сводящиеся к уравнениям с
разделяющимися переменными
.
Дифференциальные
уравнения, сводящиеся к уравнениям с
разделяющимися переменными ![]() , a
≠ 0, b ≠ 0.
Дифференциальные
уравнения, сводящиеся к уравнениям с
разделяющимися переменными
, a
≠ 0, b ≠ 0.
Дифференциальные
уравнения, сводящиеся к уравнениям с
разделяющимися переменными  или
или  .
Дифференциальные
уравнения, сводящиеся к уравнениям с
разделяющимися переменными
.
Дифференциальные
уравнения, сводящиеся к уравнениям с
разделяющимися переменными 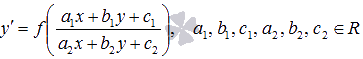 .
.