4.3.1.2. Стандарт неизвестен.

Однако в большинстве случаев стандарт неизвестен, а из выборки определена только его оценка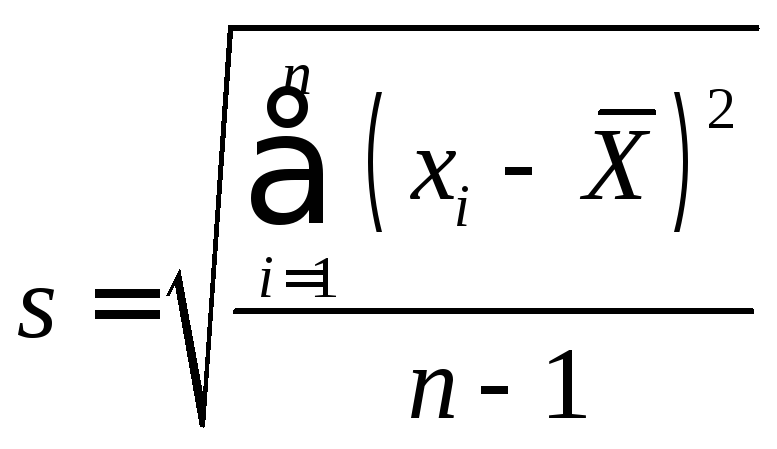. В этом случае можно воспользоваться статистикой

. Эта безразмерная случайная величина распределена по закону Стьюдента с числом степеней свободы . В таблицах обычно приводятся значениясоответствующие вероятности. Поэтому для доверительной вероятностисимметричный доверительный интервал получаем из тождества:

,

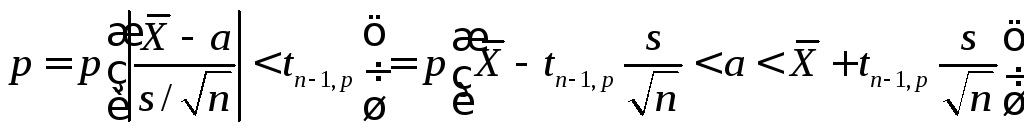т.е. с вероятностью интервалсодержит искомое значение. В этом случае полуширина интервала

Таблица 4.2. Значения соответствующие вероятности

.для распределения Стьюдента.

\	0,8	0,9	0,95	0,99	0,999
1	3,08	6,31	12,71	63,66	636,61
2	1,89	2,92	4,30	9,92	31,60
4	1,53	2,13	2,78	4,60	8,61
8	1,40	1,86	2,31	3,36	5,04
16	1,34	1,75	2,12	2,92	4,02
32	1,31	1,70	2,04	2,74	3,64
	1,28	1,64	1,96	2,58	3,29

В Excel значение можно получить двумя способами. Во-первых, в менюСервисАнализ данныхможно воспользоваться описанной ранее функцией Описательная статистика и указать значение доверительной вероятности. Недостаток этого способа – за выборку принимается либо строка, либо столбец, а таблица воспринимается как набор разных выборок. Впрочем, данные, представленные в виде таблицы, путём переноса нетрудно расположить в виде строки или столбца, и после этого применить Описательную статистику. Ниже приведён результат обработки таким образом массива результатов лабораторного практикума (стр. )

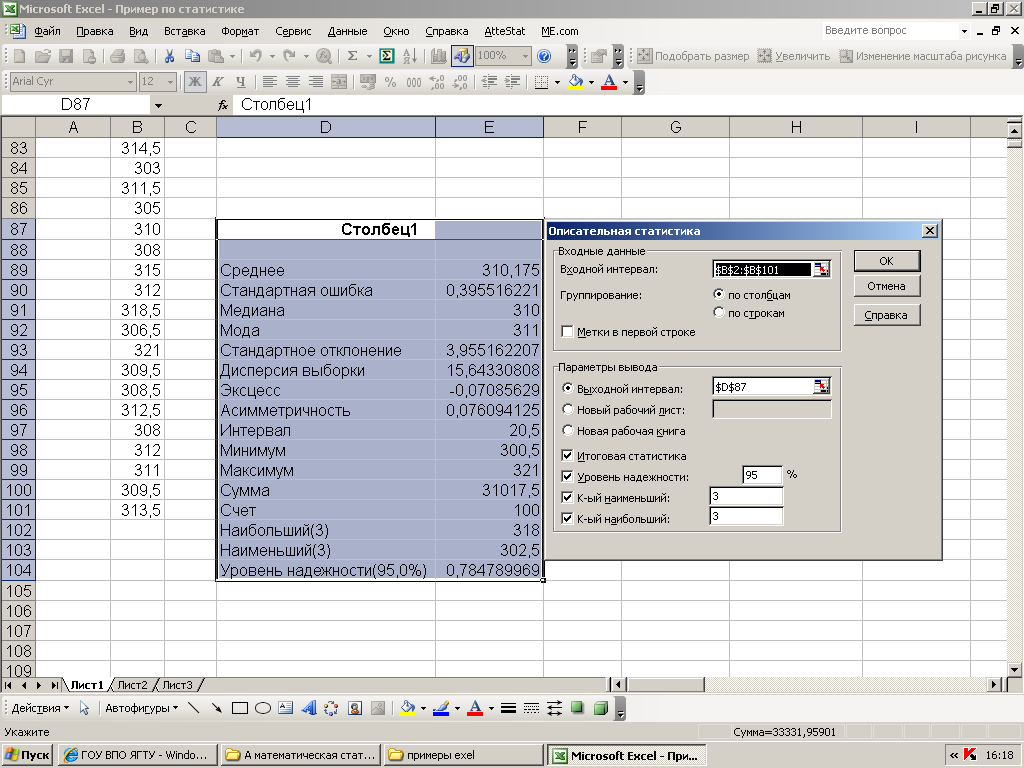
Полуширина доверительного интервала, с заданной доверительной вероятностью, которая здесь называется уровнем надёжностью, выводится в последней строке таблицы результатов выполнения этой программы.

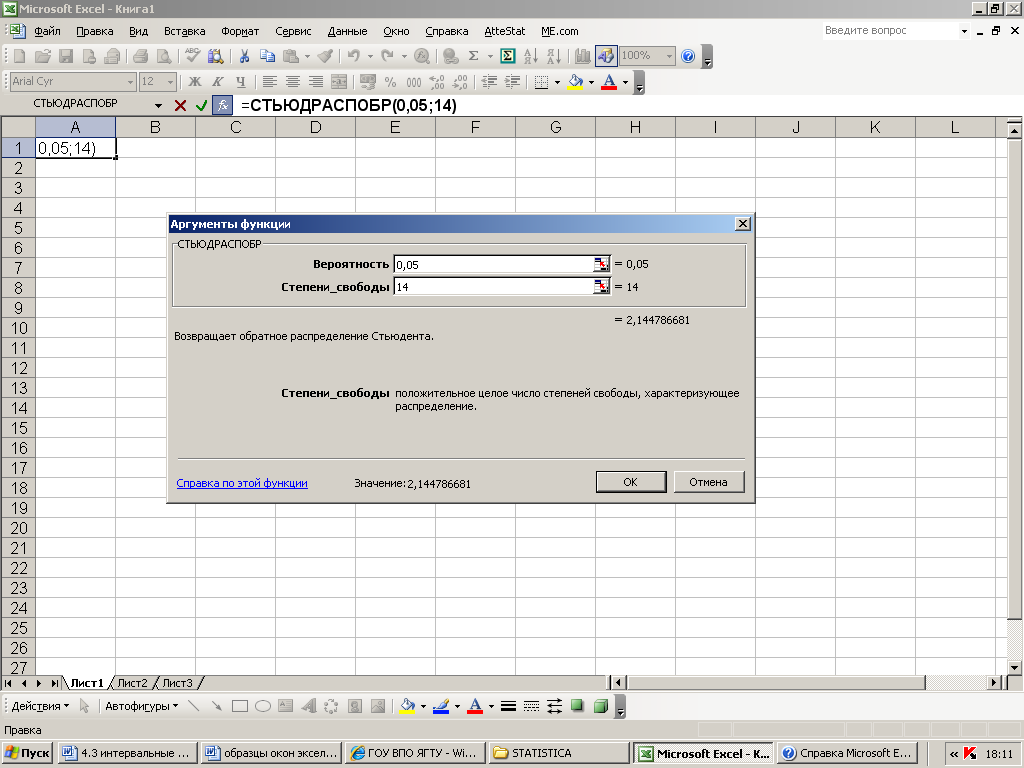
Второй путь: получить значение функциейСТАНДОТКЛОН, значение - функциейСТЬЮДРАСПОБР, после чего вычислить и .

4.3.2. Доверительный интервал для дисперсии нормального распределения

Так как наилучшей точечной оценкой является величина:

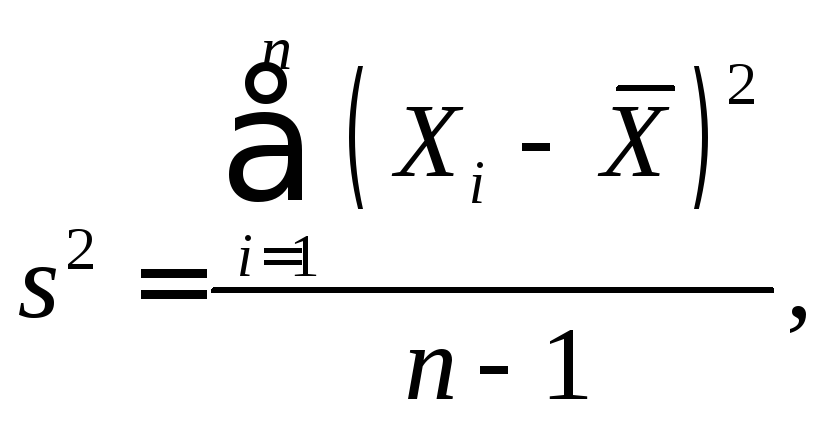
а сумма 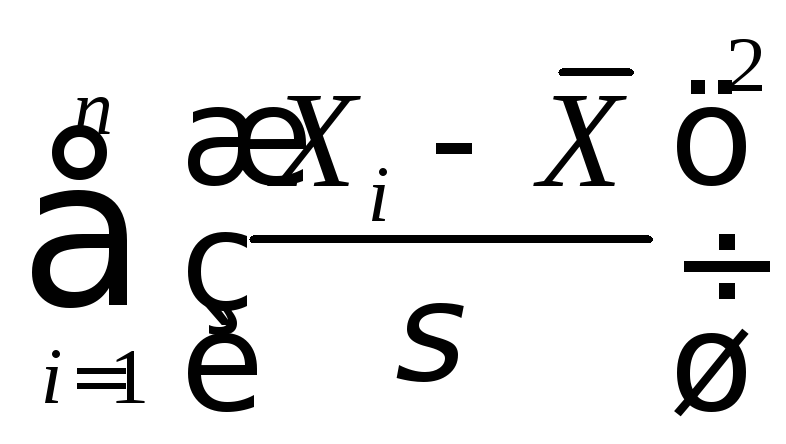имеет распределениесстепенью свободы, поэтому и статистикараспределена по тому же закону, и мы для нахождения доверительного интервала, соответствующего доверительной вероятностиможем воспользоваться соотношением

.

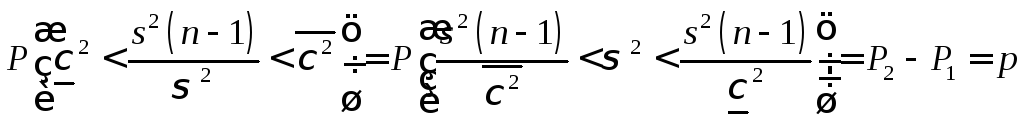Если в таблицах указаны значения , соответствующие вероятноститосоответствует значению, а- значению. Задавая различные значения, мы, естественно, будем получать различные интервалы, содержащие значенияс одной и той же вероятностью. Наилучшим среди них считается такой, для которого вероятность накрытия любого другого значенияменьше или равна. Запишем такой интервал в виде. Коэффициентыидля нижней и верхней границ такого интервала приведены в таблице:

Таблица 4.3.

	Надёжность
	0,90		0,95		0,99
2	0,25	11,93	0,21	23,61	0,15	114,20
3	0,31	6,30	0,27	10,13	0,20	29,69
4	0,36	4,53	0,31	6,59	0,24	15,15
5	0,40	3,69	0,35	5,05	0,27	9,93
6	0,43	3,20	0,38	4,21	0,30	7,57
7	0,46	2,88	0,40	3,68	0,32	6,24
8	0,48	2,65	0,42	3,31	0,34	5,30
9	0,50	2,48	0,44	3,05	0,36	4,68
10	0,51	2,35	0,46	2,84	0,38	4,24
11	0,53	2,24	0,48	2,68	0,39	3,90
12	0,54	2,15	0,49	2,55	0,40	3,64
13	0,56	2,08	0,50	2,44	0,42	3,42
14	0,57	2,02	0,51	2,35	0,43	3,24
15	0,58	1,96	0,52	2,27	0,44	3,09
16	0,59	1,92	0,53	2,21	0,45	2,96
17	0,59	1,88	0,54	2,15	0,46	2,83
18	0,60	1,84	0,55	2,10	0,47	2,74
19	0,61	1,80	0,56	2,05	0,48	2,66
20	0,62	1,78	0,57	2,01	0,49	2,57
22	0,63	1,72	0,58	1,93	0,50	2,45
24	0,64	1,68	0,59	1,88	0,52	2,34
26	0,65	1,64	0,61	1,82	0,53	2,26
30	0,67	1,58	0,63	1,74	0,55	2,12
34	0,69	1,54	0,64	1,68	0,57	2,01
39	0,70	1,49	0,66	1,62	0,59	1,91