4.2 Точечные оценки параметров распределений.

Итак, у нас есть выборка объёма и мы решили, какой функцией описывать распределение генеральной совокупности. Эта функция содержит ряд неизвестных параметров, набор которых обозначим символом. Эти параметры мы и должны определить по данным выборки. Ясно, что их точное значение мы в принципе не можем определить, поскольку любая функция случайных величин есть величина также случайная. Самое большее, что мы можем сделать – это найти их в каких-то смыслах наилучшее приближённое значение, которое и назовём точечной оценкой. К этой случайной величине разумно предъявить ряд требований, которые желательно выполнять.

Желательно, во-первых, чтобы математическое ожидание совпадало с действительным значением. Оценка, обладающая этим свойством, называетсянесмещённой.

Во-вторых, хотелось бы, чтобы при увеличении объёма выборки вероятность сколь угодно малых отклонений приближалась к 1, т.е. для любого

Такое свойство оценки называют состоятельностью.

В-третьих, желательно, чтобы дисперсия оценки была бы как можно меньше. Это свойство называется эффективностью оценки.

Для анализа выборки удобно рассматривать набор вариант не какпоследовательных значений одной и той же случайной величины, а как реализацию случайного вектора сстатистически независимыми (если выборка произведена должным образом) компонентами. Напомним, что в этом случае многомерная плотность вероятности или вероятность равна произведению соответствующих одномерных величин.

4.2.1. Оценка математического ожидания.

Предположим, что все имеют одинаковые математические ожидания,, но, возможно, различные стандарты. Такая ситуация бывает, например, тогда, когда одну и ту же величину измеряют различными методами с различной точностью. Будем искать оценкув виде линейной комбинации вариант. Для того, чтобы эта оценка была несмещённой, необходимо, чтобы. Таким образом, любая линейная комбинация вариант, сумма коэффициентов которой равна единице, будет несмещённой оценкой математического ожидания. Эти коэффициенты называют статистическими весами соответствующих им вариант.

Найдём теперь её дисперсию . Для обеспечения эффективности требуется найти минимум этой функции при условии, что. Для этого составляем функцию Лагранжаи приравниваем нулю все её производные. В результате получаем систему:

,

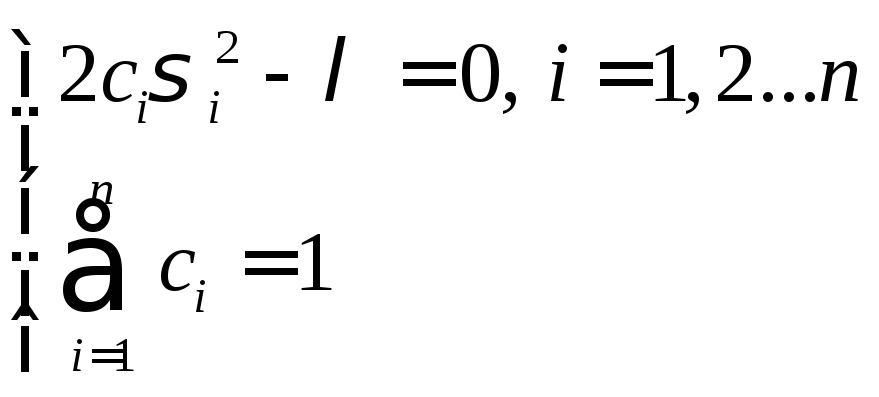из которой находим искомые значения коэффициентов:

.

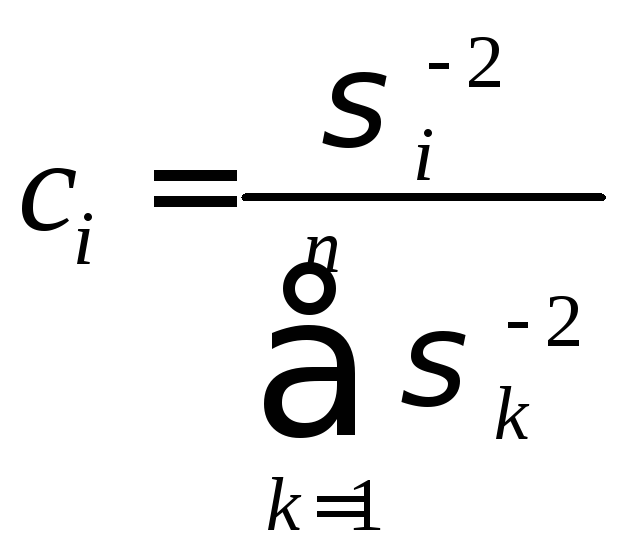Таким образом, веса оказываются обратно пропорциональными дисперсиям. Такой результат согласуется с нашим здравым смыслом: чем точнее измерения, тем больше мы им доверяем.

Итак, оценка

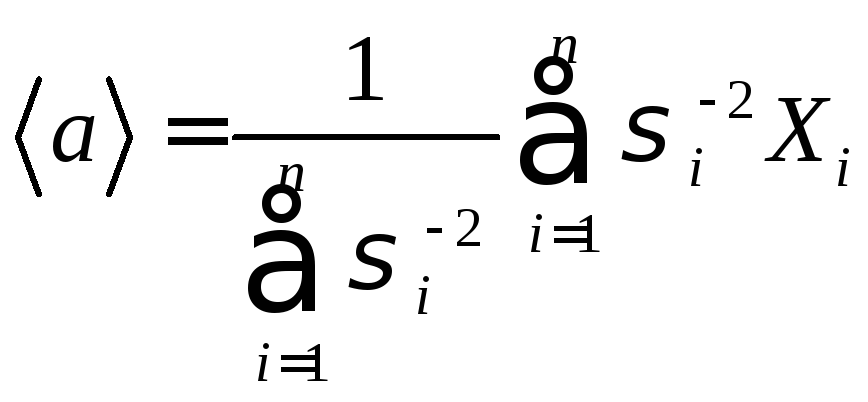
является несмещённой эффективной оценкой математического ожидания. Для проверки её состоятельности найдём дисперсию:

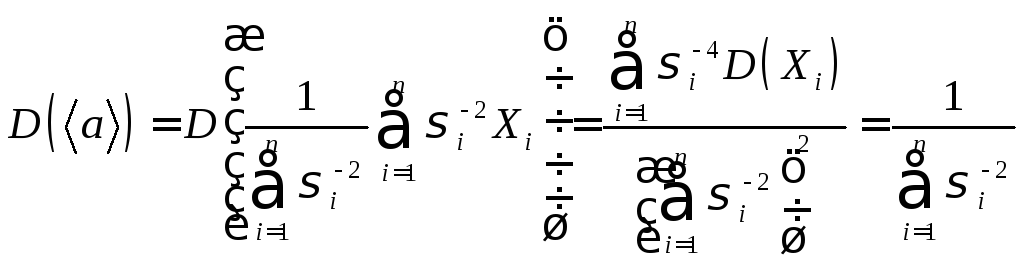
С ростом числа слагаемых в знаменателе сумма неограниченно возрастает, при, что и подтверждает состоятельность этой оценки.

Если все стандарты одинаковы, то:

,

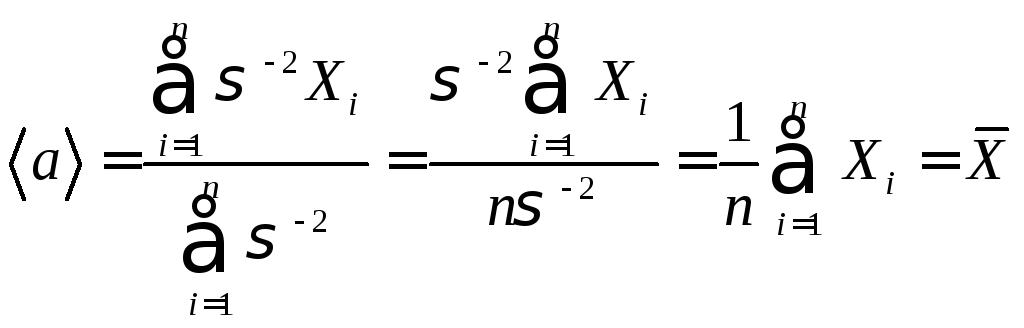В этом случае несмещённой эффективной и состоятельной оценкой математического ожидания будет среднее выборки.

4.2.2. Метод максимального правдоподобия

Этот метод получения оценок параметров распределений основан на том, что коль скоро мы получили определённую выборку, то вероятность её появления, скорее всего, близка к максимуму вероятности (в случае дискретных) или её плотности (в случае непрерывных спектров). Если мы запишем выражение для вероятности или её плотности с искомыми параметрами и подставим в неё данные выборки, то задача нахождения оценок сводится к задаче поиска точек экстремума этой функции параметров, которую называют функцией правдоподобия. Поскольку во многих случаях эта функция представляет собой произведение и степени ряда сомножителей, то удобнее искать максимум её логарифма. Натуральный логарифм – монотонно возрастающая функция, и точки его максимума совпадают с точками максимума его аргумента. Логарифм функции правдоподобия называют обычно логарифмической функцией правдоподобия и обозначают символом .

Рассмотрим несколько примеров оценок максимального правдоподобия.

Пример 4.1. Полиноминальное распределение. Пусть доля некоторого признака (числового или качественного - безразлично) в генеральной совокупности равна. Тогда вероятность появления этого признака в случайной выборке с возвращением (а в случае, когда число элементов в генеральной совокупности много больше объёма выборки, то и в бесповторной). Если в выборке объёмапризнакимеет частоту, признак- частоту, и т.д., то в соответствии с полиноминальным законом вероятность появления такой выборки рана:

Тогда логарифмическая функция правдоподобия равна:

Для нахождения её максимума при условии составляем функцию Лагранжаи приравниваем нулю все её частные производные. В результате получаем систему:

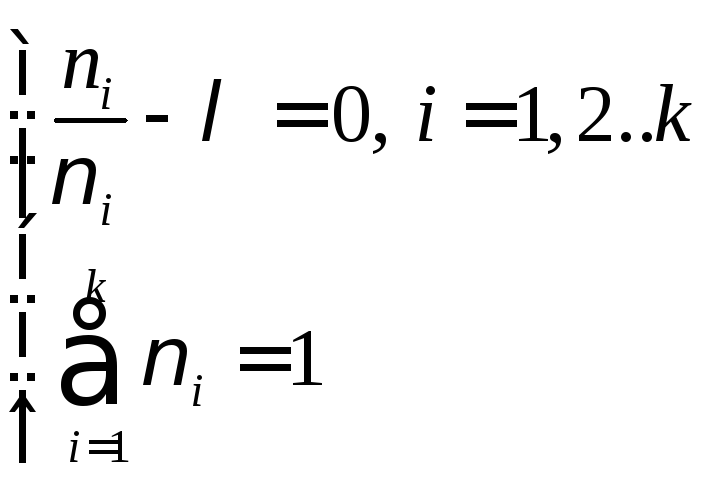
Из первыхуравнений находим, подставляя которые в последнее, получаем:откуда, и, следовательно,.

Эта оценка оказывается несмещённой, поскольку . Дисперсия этой оценкистремится к нулю с ростом, что доказывает её состоятельность.

Пример 4.2. Нормальное распределение.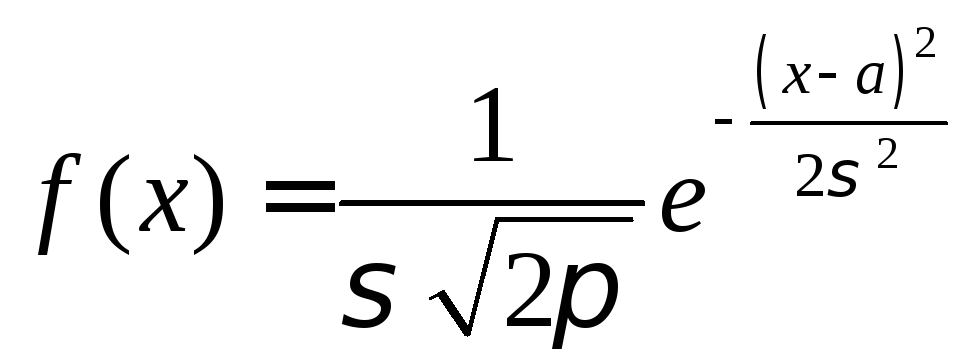, откуда

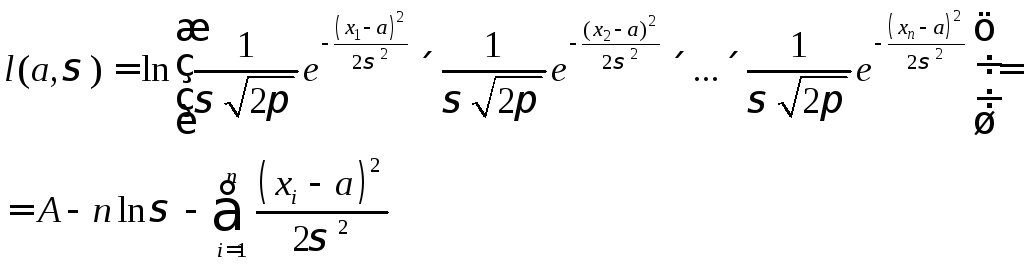
Необходимые условия максимума:

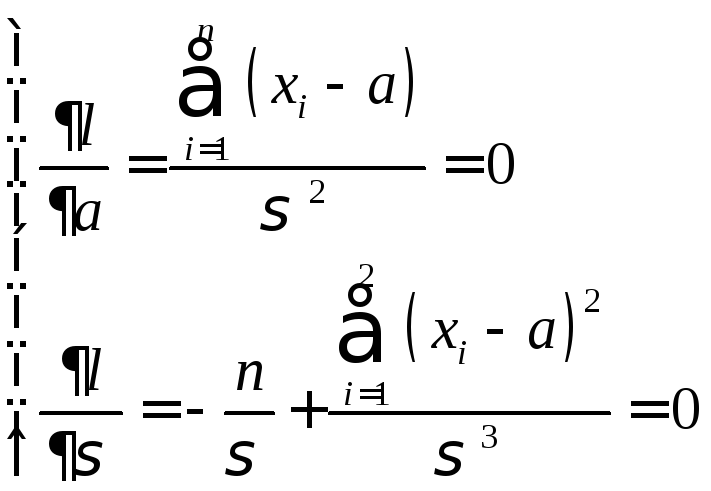
Из первого уравнения находим оценку , и из второго.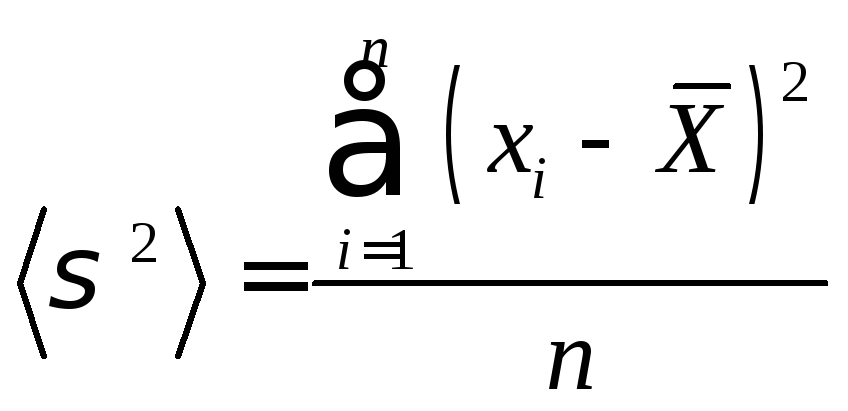

Так как параметр в нормальном распределении совпадает с математическим ожиданием, то, как следует из 4.1, его правдоподобная оценка оказывается несмещённой, состоятельной и эффективной. Что касается второй оценки, то она оказывается смещённой, поскольку:

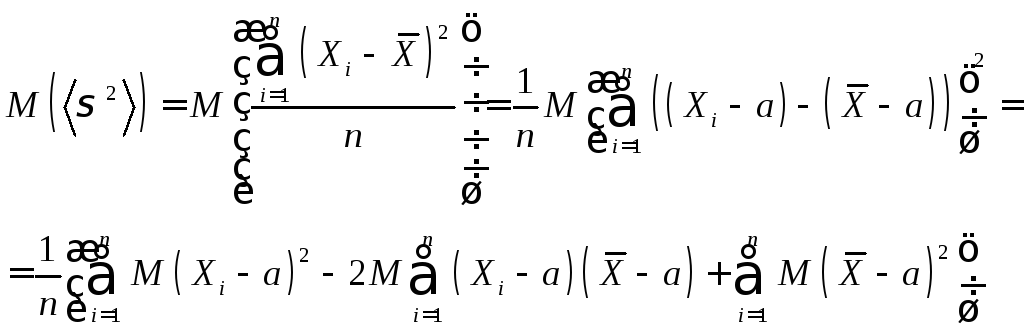
Так как ,

то:

Несмещённой оценкой является, таким образом, оценка: