4.4.2. Хи-квадрат тест.

Проверку адекватности полученной модельной функции распределения можно провести путём сравнения рассчитанных с её помощью величин с данными выборки. Стандартная процедура заключается в следующем. Выборка объёма разбивается нагрупп (интервалов), в каждой (-ом) из которыхвариант, и по найденной функции распределения рассчитываются вероятностипопадания случайной величины в эти группы (интервалы). После этого составляется статистика:

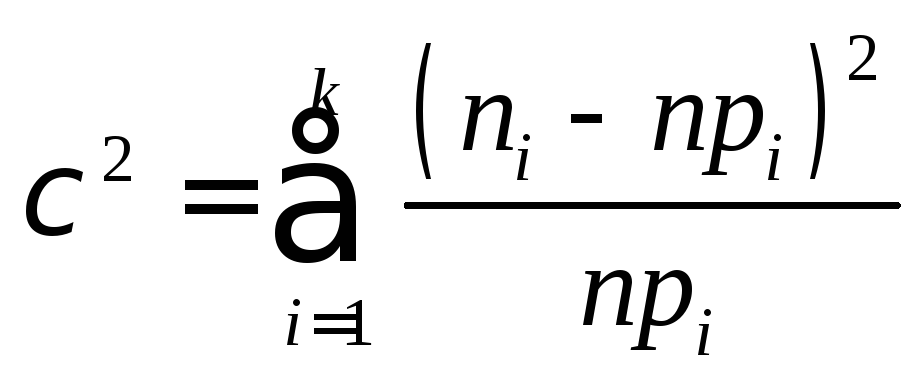
распределение которой асимптотически приближается к распределению сстепенями свободы. (-число групп (интервалов),-число параметров распределения, найденных по выборке). Очевидно, чем меньше вычисленное значение, тем лучше полученная функция распределения описывает распределение как выборки так и генеральной совокупности. Однако, поскольку- случайная величина, надо определиться, до какого её значения полученное описание можно считать адекватным. Для установления этого предельного значения необходимо, как и при построении доверительного интервала, задаться некоторой доверительной вероятностью, или уровнем значимости,и найти его по значениямив таблице значений, соответствующих вероятностям,

Найденную функцию распределения можно считать адекватной на уровне значимости , еслиокажется меньше табличного значения.

Следует иметь в виду, что слишком малые значения недопустимы. Поэтому, если в какой-то группе оно окажется меньше пяти, её надо объединить с соседней.

В Excel такую проверку легко сделать с применением функции ХИ2ТЕСТ из меню «Статистические».

Предварительно с помощью функции ЧАСТОТА надо сформировать

массив частот, а с помощью ХХХХРАСПР – массив соответствующих значений интегральной функции распределения. Далее, путём вычитания смежных значений интегральной функции, следует получить массив вероятностей, а умножая эти вероятности на общее число вариант – массив теоретических частот np(i) . Затем в окошко Фактический интервал диалогового окна ХИ2ТЕСТ вводим массив Частота, а в окошко Ожидаемый интервал – массив np(i). Функция возвращает вероятность того, что значения могут превышать рассчитанные по выборке. С определёнными оговорками эту величину можно принять за вероятность того, чтовыборочное распределение не противоречит модельному. Ниже приведён результат применения ХИ2ТЕСТ к массиву результатов химического анализа, полученных группой студентов. При этом значения F(x) рассчитывались функцией НОРМРАСПР с параметрами, рассчитанными по этой выборке.

Карман	Частота	F(x)		p(i)=F(x(i))-F(x(i-1)	np(i)
3	4	0,040059		0,040059157	4,005915686
6	12	0,158655		0,118596097	11,85960971
9	23	0,401294		0,24263842	24,26384204
12	31	0,691462		0,290168787	29,0168787
15	20	0,89435		0,202887765	20,28877651
18	8	0,97725		0,082899642	8,289964172
21	2	0,99702		0,019770369	1,977036871
хи-квадрат
0,999802