1.Генеральная совокупность и выборка.

Математическая статистика – это раздел математики, в котором разработаны методы обработки результатов экспериментов, наблюдений, социологических опросов с позиций теории вероятностей. Все возможные, (по крайней мере, мысленно – возможные) результаты изучения какого-либо объекта рассматриваются как значения некоторой случайной величины с неизвестным распределением. Это множество носит название генеральной совокупности. В большинстве случаев выводы о генеральной совокупности приходится делать по некоторому конечному числу полученных значений этой случайной величины, которые называются вариантами, а их множество - выборкой. Выборка должна производиться таким образом, чтобы правильно характеризовать генеральную совокупность,- быть, как говорят, репрезентативной. Для этого она должна быть случайной. Это обеспечивается специальными процедурами получения данных.

2. Формы представления выборки.

Из наблюдений или измерений мы получаем выборку случайных чисел – вариант. Числоназываютобъёмом выборки, а разность между максимальным и минимальным значением – её размахом. Расположив варианты по возрастанию их значений, мы получим ранжированный вариационный ряд. Если число вариант велико, то данные следует структурировать. В случае, когда несколько вариант имеют одинаковое значение, можно представить их в виде таблицы:

			……………
			………………

Такая таблица называется дискретным вариационным рядом. В её верхней строке указывается различных значений вариант в порядке их возрастания, а в нижней – числа повторений этих значений –частоты. Очевидно, сумма частот равна объёму выборки, . Отношениеназываютчастостью варианта ;. Если число столбцов в ней оказывается слишком большим, то несколько соседних значений вариант можно объединить в общий интервал. Тогда в первой строке будут указываться интервалы, а во второй – число вариант, попадающих в соответствующий интервал. Такое представление данных называютинтервальным вариационным рядом. Чаще всего строят равные интервалы, а их число принимают близким числу. Тогда ширина интервала равна.

Для наглядного представления дискретных вариационных рядов строят полигоны – ломаные линии, составленные из отрезков, соединяющих точки с координатами и. Интервальные вариационные ряды представляют в видегистограмм –наборов прямоугольников, основания которых – соответствующие интервалы, отложенные по оси абсцисс, а высоты – соответствующие частоты, или частости. Если интервалы имеют разную ширину, то высоты прямоугольников устанавливается равными отношению, или. Последнюю величину можно рассматривать как аналог плотности вероятности .

Сумму накопленных частостей называютвыборочной функцией распределения. Очевидно, она является аналогом интегральной функции распределения вероятностей. Её график называется кумулятой.

3. Числовые характеристики выборки.

3.1. Описательные статистики

Любая функция вариант называется статистикой. Для сжатого описания выборки используют статистики, аналогичные числовым характеристикам распределений случайных величин.

Модой выборки называют значение варианта с максимальной частотой. Если выборка представлена интервальным вариационным рядом с равными интервалами, то значение моды принимают равным середине интервала с максимальной частотой. При различной ширине интерваловэту величину принимают равной середине интервала с максимальной плотностью вариант.

Медианой выборки МЕ(Х) называют такое значение признака, для которого доля вариант с меньшей его величиной равна половине.

Квартилями выборки (нижним и верхним)называют такие значения признака, для которых доля вариант с меньшей его величиной составляет одну четверть для и три четверти для ..

Средним (арифметическим) значением выборки называют величину .

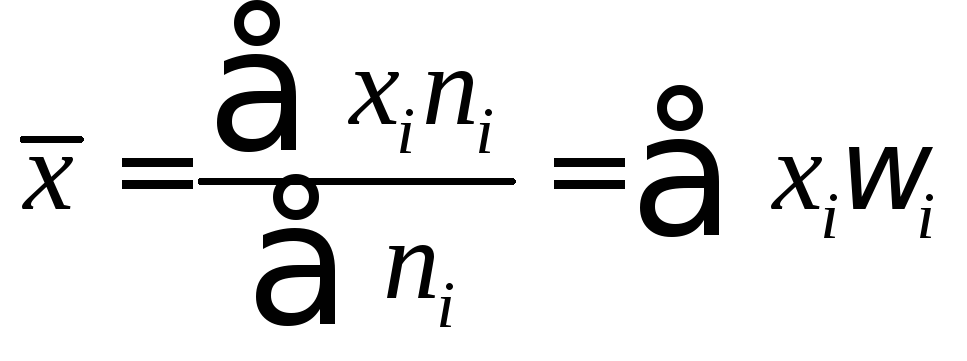При обработке интервальных вариационных рядов за принимают серединуого интервала.

Выборочным моментом ого порядка называют величину .

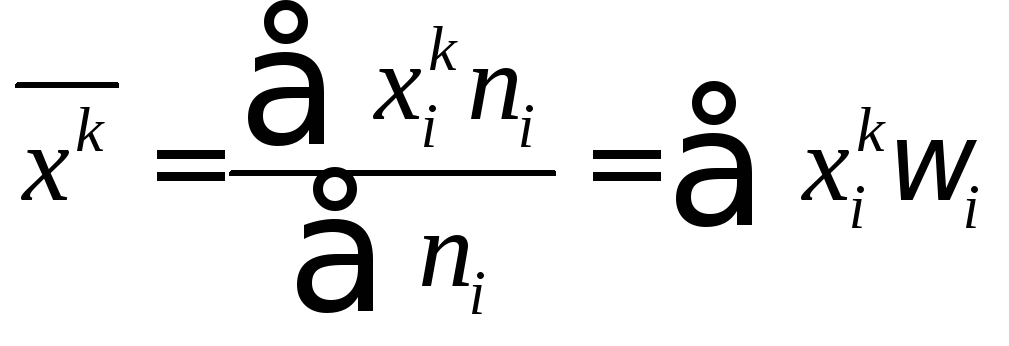Выборочным центральным моментом – величину .

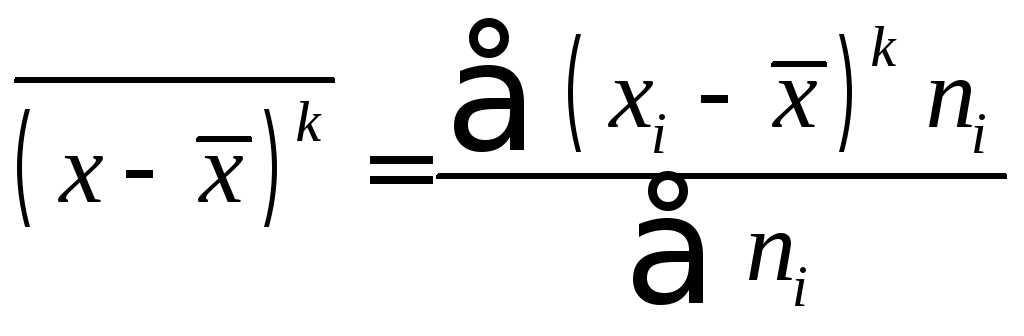Выборочной дисперсией –величину .

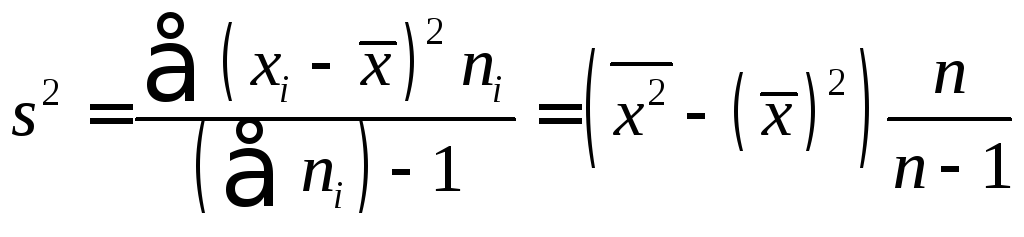Выборочной асиметрией – величину .

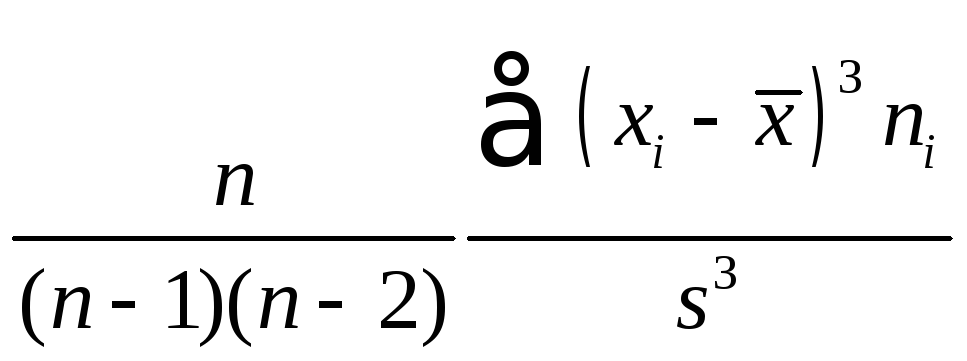Выборочным эксцессом – величину .

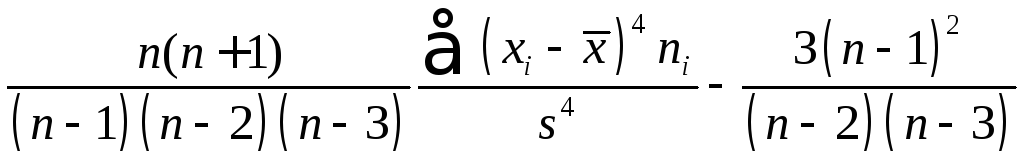Последние две величины служат для сравнения выборочного распределения с нормальным.