- •Элементы
- •5.1. Проверка гипотез о параметрах распределений.
- •5.1.1. Проверка значения математического ожидания нормального распределения.
- •5.1.2. Проверка значения дисперсии нормального распределения.
- •5.1.3. Проверка значения доли (параметра биноминального распределения).
- •5.2. Сравнение выборок
- •5.2.1. Сравнение дисперсий
- •5.2.2. Сравнение средних двух независимых выборок
- •5.2.3. Сравнение средних парных выборок.
- •5.2.4. Сравнение долей (параметра биноминального распределения)
- •5.3. Проверка однородности выборок.
- •5.4. Дисперсионный анализ (anova)
- •5.4.1. Однофакторный дисперсионный анализ.
- •5.4.2. Многофакторный дисперсионный анализ.
Элементы
МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ
Часть 2.
Статистические гипотезы.
Сравнение выборок.
5.Статистические гипотезы и их проверка.
Статистическими
гипотезами называются различные
предположения, справедливость которых
можно доказать или опровергнуть путём
обработки выборочных статистических
данных. Рассмотренная в предыдущем
параграфе процедура проверки адекватности
функции распределения является примером
проверки одной из статистических гипотез
- гипотезы о виде функции распределения.
Ясно, что поскольку мы имеем дело со
случайными величинами, то и выводы
относительно справедливости той или
иной гипотезы будут неоднозначными.
Предположим, что некоторая гипотеза
![]() верна, а мы на основании выборочных
данных её отвергли. При этом мы совершили
ошибку, которую принято называтьошибкой
первого рода.
Вероятность такой ошибки называют
уровнем
значимости
верна, а мы на основании выборочных
данных её отвергли. При этом мы совершили
ошибку, которую принято называтьошибкой
первого рода.
Вероятность такой ошибки называют
уровнем
значимости
![]() .
С другой стороны, мы можем ошибочно
принять гипотезу
.
С другой стороны, мы можем ошибочно
принять гипотезу![]() ,
в то время, как на самом деле верна другая
гипотеза
,
в то время, как на самом деле верна другая
гипотеза![]() ,
которую называютальтернативной.
В этом случае мы совершим ошибку
второго рода,
вероятность которой
,
которую называютальтернативной.
В этом случае мы совершим ошибку
второго рода,
вероятность которой
![]() .
.
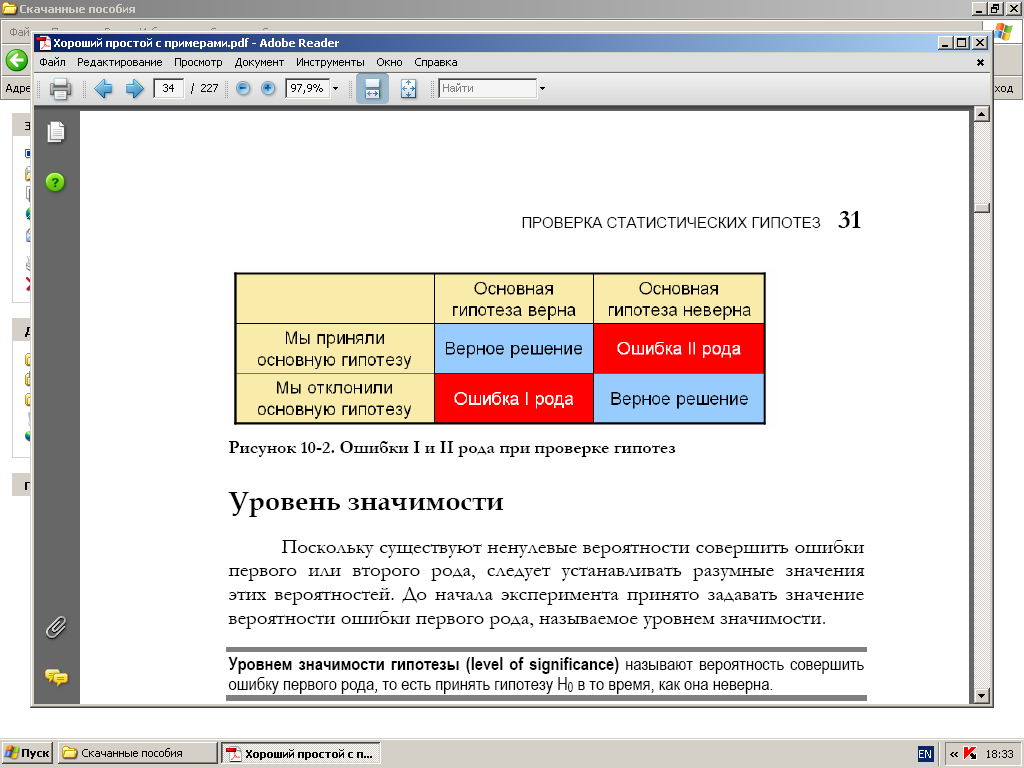
Конечно, желательно
вероятности обеих этих ошибок свести
к минимуму. К сожалению, это невозможно,
поскольку с уменьшением вероятности
ошибки первого рода при фиксированном
объёме выборки увеличивается ошибка
второго рода. Поэтому на практике
ограничиваются только заданием допустимой
вероятности ошибки первого рода на
уровне
![]() 0,05
или 0,01, а анализ вероятности ошибки
второго рода производят по мере
необходимости в ответственных случаях.
0,05
или 0,01, а анализ вероятности ошибки
второго рода производят по мере
необходимости в ответственных случаях.
Процедуру
проверки гипотезы начинают с расчёта
значения
![]() некоторой
функции выборки, которую называюткритерием.
Множество значений этой функции разбивают
на два подмножества
некоторой
функции выборки, которую называюткритерием.
Множество значений этой функции разбивают
на два подмножества
![]() -область
принятия решения
и
-область
принятия решения
и
![]() -критическое
множество таким
образом, чтобы вероятность
-критическое
множество таким
образом, чтобы вероятность
![]() ,
а
,
а![]() .
Если вычисленное значение
.
Если вычисленное значение![]() попадает
в
попадает
в![]() ,
то гипотеза
,
то гипотеза![]() принимается на уровне значимости
принимается на уровне значимости![]() (снадёжностью
(снадёжностью
![]() ) если в
) если в![]() -
то отвергается. В зависимости от характера
альтернативной гипотезы критическое
множество
-
то отвергается. В зависимости от характера
альтернативной гипотезы критическое
множество![]() выбирают либо односторонним (
выбирают либо односторонним (![]() или
или![]() ),
либо двусторонним (
),
либо двусторонним (![]() и
и![]() ,
,![]() ).
).
5.1. Проверка гипотез о параметрах распределений.
5.1.1. Проверка значения математического ожидания нормального распределения.
Если известно,
что варианты выборки распределены по
нормальному закону
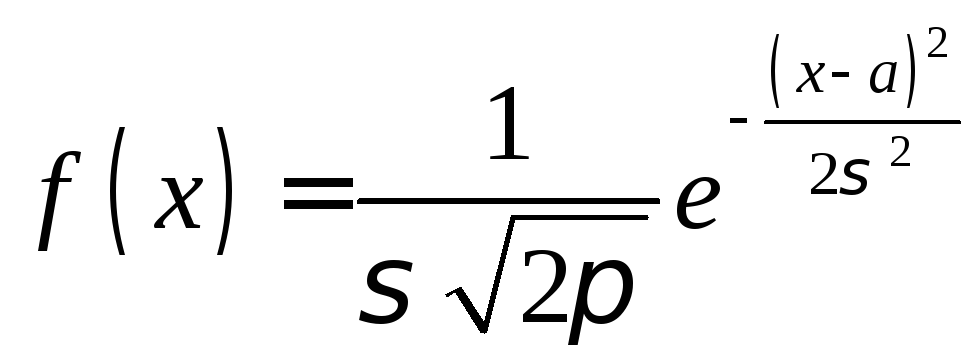 ,
стандарт которой неизвестен, то для
проверки гипотезы
,
стандарт которой неизвестен, то для
проверки гипотезы![]() в качестве критерия можно использовать
статистику
в качестве критерия можно использовать
статистику
![]()
Эта статистика
имеет распределение Стьюдента с числом
степеней свободы
![]() .
Поэтому при альтернативной гипотезе
.
Поэтому при альтернативной гипотезе![]() гипотезу
гипотезу![]() можно отвергнуть, если
можно отвергнуть, если![]() (двусторонняя
критическая область). Если альтернативная
гипотеза
(двусторонняя
критическая область). Если альтернативная
гипотеза![]() ,
то нулевая гипотеза принимается при
условии
,
то нулевая гипотеза принимается при
условии![]() ,
а при
,
а при![]() - при условии
- при условии![]() .
Здесь под символом
.
Здесь под символом![]() понимаются квантили распределения
Стьюдента уровня
понимаются квантили распределения
Стьюдента уровня![]() ,
т.е. числа, удовлетворяющие условию
,
т.е. числа, удовлетворяющие условию![]() .
Однако в ряде таблиц этого распределения
под символом
.
Однако в ряде таблиц этого распределения
под символом![]() понимаются значения, соответствующие
вероятности
понимаются значения, соответствующие
вероятности![]() .
При использовании этих таблиц значение
.
При использовании этих таблиц значение![]() при альтернативной гипотезе
при альтернативной гипотезе![]() соответствует значению
соответствует значению![]() ,
при
,
при![]() ,
,![]() ,
а при
,
а при![]() ,
,![]() ,
где
,
где![]() -
уровень значимости.
-
уровень значимости.
В Excel
критические
значения
![]() можно получить функциейСТЬЮДРАСПОБР
в меню
Статистические.
При этом
под словом
«вероятность» в диалоговом окне
понимается значение уровня значимости.
можно получить функциейСТЬЮДРАСПОБР
в меню
Статистические.
При этом
под словом
«вероятность» в диалоговом окне
понимается значение уровня значимости.
В качестве
примера вернёмся к рассмотрению ста
результатов измерения концентрации
студентами. Для измерений им был дан
раствор с концентрацией 309,5 мг/л, а
среднее по всем измерениям оказалось
равным 310, 185 с выборочным стандартом
3,96….. Встаёт вопрос, можно ли считать
это различие случайным, или студенты
вносят систематическую ошибку. Другими
словами, можно ли считать, что выборка
принадлежит генеральной совокупности
с параметром
![]() =309,5,
или
=309,5,
или![]() .
Сравнивая вычисленное значение с
найденным функциейСТЬЮДРАСПОБР(0,05;99)
, приходим
к
выводу, что нет оснований утверждать
о наличии систематической ошибки в
измерениях студентов.
.
Сравнивая вычисленное значение с
найденным функциейСТЬЮДРАСПОБР(0,05;99)
, приходим
к
выводу, что нет оснований утверждать
о наличии систематической ошибки в
измерениях студентов.
|
|
310,185 |
|
|
309,5 |
|
|
3,964269074 |
|
|
1,727935181 |
|
tкр.
|
1,9842169 |
При известном
стандарте вместо статистики
![]() следует использовать статистику
следует использовать статистику
![]() ,
,
распределённую
по нормальному закону
![]() .
Критические значения
.
Критические значения![]() при уровне значимости
при уровне значимости![]() для двусторонней критической области
для двусторонней критической области![]() ,
если использовать таблицы функции
,
если использовать таблицы функции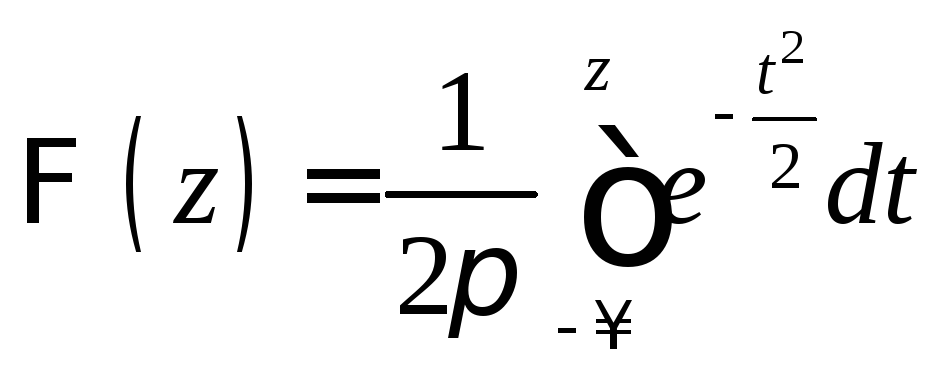 ,
и
,
и![]() -
при применении таблиц
-
при применении таблиц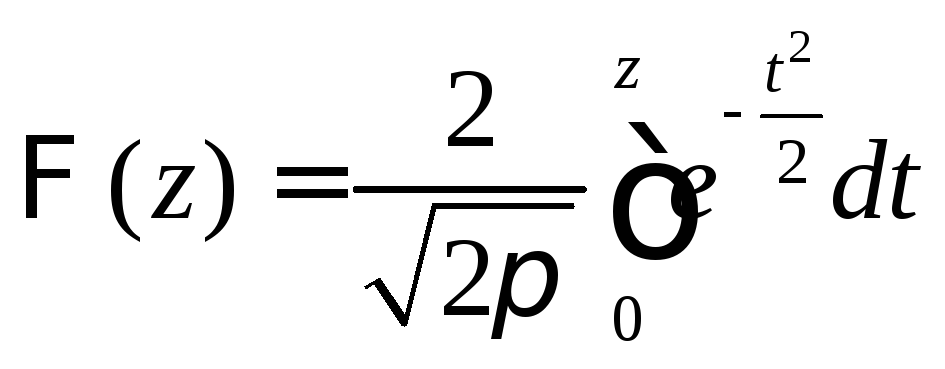 .
.
В Excel
критические
значения
![]() находятся функциейНОРМСТОБР,
в меню
Статистические.
При этом в
диалоговое окно значение вероятности
надо устанавливать равным
находятся функциейНОРМСТОБР,
в меню
Статистические.
При этом в
диалоговое окно значение вероятности
надо устанавливать равным
![]() для двусторонней критической области,
для двусторонней критической области,![]() - для правой односторонней, и
- для правой односторонней, и![]() - для левой односторонней критической
области.
- для левой односторонней критической
области.
…..Для проверки
гипотезы
![]() можно также воспользоваться функциейZТЕСТ
в меню «Статистические».
можно также воспользоваться функциейZТЕСТ
в меню «Статистические».
П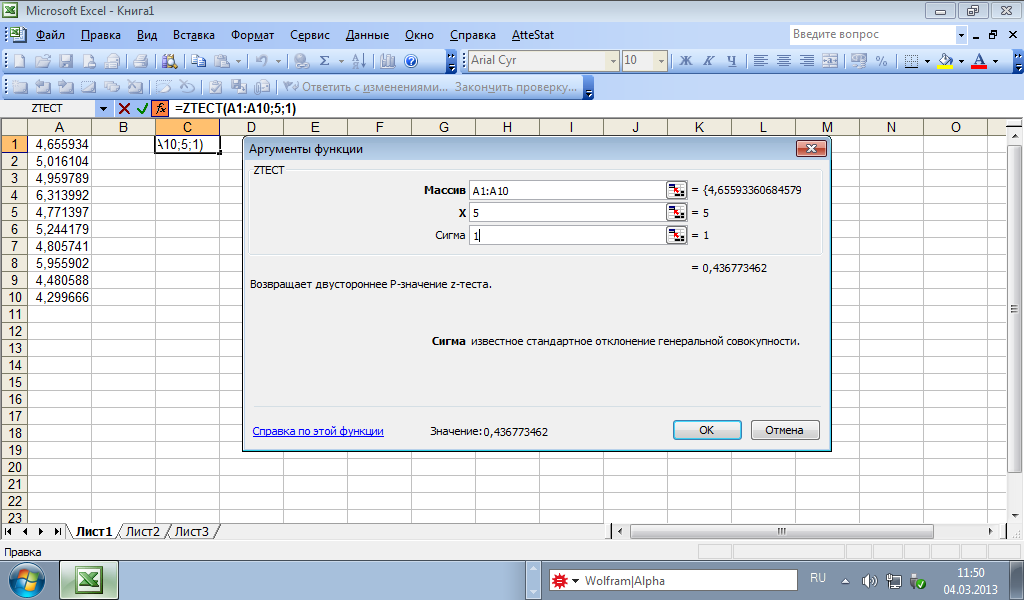 ри
использовании этой функции не надо
отдельно вычислять выборочные средние,
выборочный стандарт, и критические
значения: вводятся непосредственно
координаты массива, заданное значение
ри
использовании этой функции не надо
отдельно вычислять выборочные средние,
выборочный стандарт, и критические
значения: вводятся непосредственно
координаты массива, заданное значение![]() (в окошко «х»), и, если стандарт распределения
известен, - его значение в окно «Сигма».
Если это окно оставить пустым, то вместо
значения стандарта принимается значение
выборочного среднеквадратичного
отклонения.
(в окошко «х»), и, если стандарт распределения
известен, - его значение в окно «Сигма».
Если это окно оставить пустым, то вместо
значения стандарта принимается значение
выборочного среднеквадратичного
отклонения.
Результатом
выполнения этой функции является
значение вероятности
![]()