Методы вычислительной математики
Решение уравнений вида f(x)=0
Постановка задачи
Дано уравнение вида
f(x) = 0.
Найти один из корней этого уравнения с точностью 0.
Этапы решения задачи
Приближенное решение уравнения f(x) = 0 включает следующие этапы:
Отделение корней и выбор отрезка, на котором локализован искомый корень. Производится исследование функции f(x) для нахождения отрезков, содержащих по одному корню.
Уточнение корней. По выбранному алгоритму последовательно сужается отрезок, содержащий корень, до такой степени, пока не станет выполнять условие точности 0.
Локализация корня
На первом этапе, как правило, применяется графический метод исследования функции f(x), а способ отделения корней основан на следующей теореме:
Теорема
Если функция f(x), определяющая уравнение f(x) = 0, на концах отрезка [a;b] принимает значения разных знаков, т.е. f(a)*f(b)<0, то на этом отрезке содержится, по крайней мере, один корень уравнения.
Если функция f(x) строго монотонна, то корень на отрезке [a;b] единственный (f'(a)*f'(b)>0) .
Предварительное исследование функции f(x) начинается с выбора подмножества допустимых значений аргумента x - отрезка [a;b].
Аналитический способ
Вычисляем значение функции f(x), начиная с точки x=A, двигаясь вправо с некоторым шагом h. Если f(x)*f(x+h)<0, то на отрезке [х;x+h] существует корень:
Следовательно, отрезок [a;b] найден, причем а= x, b = x+h.
Если f(x) =0, то х* - точный корень.
Графический способ
Строится график функции f(x) и по нему вручную выбирается отрезок [a;b].
Рассмотрим реализацию этого подхода в MS Excel на примере решения уравнения:
ecos2(x)-3·sin(0,8·x)+0,5=0
Решение будем искать на отрезке [0;5,5].
Порядок решения задачи:
1 Табулирование функции
1.1 Заполнение ячеек таблицы
|
Адрес клетки |
Содержание |
Тип |
|
А1 |
Табулирование функции |
Текст |
|
А2 |
х |
Текст |
|
А3 |
0 |
Число |
|
В1 |
у |
Текст |
|
G1 |
шаг |
Текст |
|
H1 |
0,5 |
Число |
Начальное значение шага выбираем равным 0,5, так чтобы в таблице было 12 строк. Расчет шага выполняем по формуле (5,5-0)/11.
Вид листа MS Excel:
1.2 Значения аргумента х меняются по правилу арифметической прогрессии.
Устанавливаем табличный курсор в клетку А4, нажимаем на клавишу =, щелкаем указателем мыши по клетке А3 (предыдущее значение аргумента), нажимаем на клавишу +, щелкаем указателем мыши по клеткеH1.
Вид листа MS
Excel:
1.3 Адрес ячейки H1, содержащей значение шага должен быть абсолютным, поэтому нажимает функциональную клавишуF4.Окончательно имеем:
|
Адрес клетки |
Содержание |
Тип |
|
А4 |
=A3+$H$1 |
Формула |
Вид листа MS Excel:
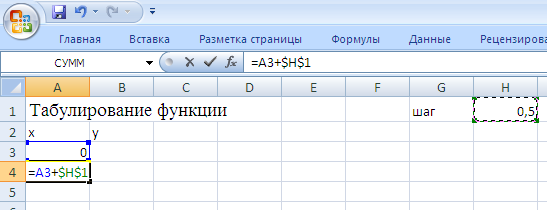
1.4 Завершаем ввод формулы нажатием на клавишу Ввод.Устанавливаем табличный курсор в клетку А4, а указатель мыши на маркер заполнения.
Вид листа MS Excel:
1.5 Нажимаем левую кнопку мыши и, не отпуская ее, перемещаем мышь в клетку А14. Вид листа MS Excel:
1.6 Вводим формулу ecos2(x)-3·sin(0,8·x)+0,5 в клетку В3.
|
Адрес клетки |
Содержание |
Тип |
|
В3 |
=EXP(COS(A3)^2)-3*SIN(0,8*A3)+0,5 |
Формула |
Вид листа MS Excel:
1.7 Заполняем значения функции столбец В в режиме копирования формулы, так как это выполнено в пунктах 1.4, 1.5.
Вид листа MS Excel:
2 Графическая интерпретация
2.1 Графическая интерпретация данных начинается с выделения диапазона А2:В14, включая названия столбцов х и у в клетках А2 и В2.
Вид листа MS Excel:
2.2 Выбор типа диаграммы. Переключаемся на страницу Вставка, выбираем категорию диаграммы –Точечная, тип – Точечная с гладкими кривыми.
Внимание! Тип диаграммы Точечная, а не График.
Вид листа MS Excel:
2.3 Вид листа MS Excel после построения диаграммы:
3 Отделение корней.
По графику видно, что на отрезке [ 0; 5,5] есть два корня:
первый корень локализован на отрезке [ 0,5; 1,5];
второй корень локализован на отрезке [ 2; 3].
Приближенные методы решения уравнения f(x) = 0