Реализация симплекс метода

Симплекс-метод был разработан и впервые применен для решения задач в 1947 г. американским математиком Дж. Данцигом. Это метод универсален. Он позволяет решить любую задачу линейного программирования.

Геометрический смысл симплексного метода состоит в последовательном переходе от одной вершины многогранника ограничений к соседней, в которой целевая функция принимает лучшее или, по крайней мере, не худшее значение до тех пор, пока не будет найдено оптимальное решение. Имея систему ограничений, приведенную к канонической форме (все функциональные ограничения имеют вид равенств), находят любое базисное решение этой системы, заботясь только о том, чтобы найти его как можно проще. Если первое же найденное базисное решение оказалось допустимым, то проверяют его на оптимальность. Если оно не оптимально, то осуществляется переход к другому, обязательно допустимому базисному решению. Симплексный метод гарантирует, что при этом новом решении целевая функция, если и не достигнет оптимума, то приблизится к нему. С новым допустимым базисным решением поступают так же, пока не найдено решение, которое является оптимальным.

Реализация симплекс метода состоит из трех основных элементов:

1) способа определения какого-либо первоначального допустимого базисного решения задачи;

2) правила перехода к лучшему решению;

3) критерия проверки оптимальности найденного решения.

Симплексный метод включает в себя ряд этапов и может быть сформулирован в виде четкого алгоритма. Это позволяет успешно программировать и реализовывать его на ЭВМ. Задачи с небольшим числом переменных и ограничений могут быть решены симплексным методом вручную.

Алгоритм симплекс метода

1 Формулировка ЗЛП.

2 Приведение задачи к канонической форме, то есть систему ограничений необходимо привести к виду:

a₁₁x₁ + a₁₂x₂ + ... + a_1nx_n + x_n+1= b₁,

a₂₁x₁ + a₂₂x₂ + ... + a_2nx_n + x_n+2= b₂,

...

a_m1x₁ + a_m2x₂ + ... + a_mnx_n + x_n+m = b_m.

3 Получение первого допустимого базисного решения (построение исходной симплекс-таблицы). Использование симплекс-таблиц наиболее удобно при ручной реализации симплексного метода. Исходная симплекс-таблица соответствует первому допустимому базисному решению. В качестве такового проще всего взять допустимое решение, в котором свободными переменными являются x₁, … , x_n, а базис образуют дополнительные переменные x_n+1, x_n+2, ..., x_n+m. Ниже приведена исходная симплексная таблица в общем виде.

Общий вид исходной симплекс-таблицы

базис	переменные							bi
	x1	x2	...	xn	xn+1	...	xn+m
xn+1	a11	a12	...	a1n	1	0	0	b1
xn+2	a21	a22	...	a2n	0	...	0	b2
...	...	...	...	...	...	...	...	...
xn+m	am1	am2	...	amn	0	0	1	bm
cj	c1	c2	...	cn	0	0	0	L

Итак, в левом столбце записываются основные (базисные) переменные, в первой строке таблицы перечисляются все переменные задачи. Крайний правый столбец содержит свободные члены системы ограничений b₁, b₂, ..., b_m. В последней строке таблицы (она называется оценочной) записываются коэффициенты целевой функции, а также значение целевой функции (с обратным знаком) при текущем базисном решении L=-f(x). В рабочую область таблицы (начиная со второго столбца и второй строки) занесены коэффициенты a_ij при переменных системы ограничений.

Замечание! Вид таблицы может быть другим, но это не меняет сути выполняемых действий.

В первом базисном решении свободные переменные x₁ , … , x_n равны нулю. Базисные переменные отличны от нуля и получаются как результат решения системы ограничений: x_n+1= b₁; x_n+2= b₂; … ; x_n+m= b_m. Данное базисное решение является допустимым. Естественно, что значение целевой функции в этом случае равно нулю, так как в формировании целевой функции участвуют переменные, которые для данного базисного решения являются неосновными.

4 Проверка условия: все c_j ≤ 0. Если «НЕТ» - осуществляется переход к пункту 5, если «ДА» - задача решена. Таким образом, на данном шаге проверяется наличие положительных элементов в последней строке симплексной таблицы. Если такие элементы имеются, необходимо продолжать решение.

5 Выбор разрешающего столбца (переменной, вводимой в базис). Разрешающий столбец выбирается в соответствии со следующим условием: c_r=max{c_j}, j=1, … , n+m, где r - номер разрешающего столбца. Таким образом, при определении разрешающего столбца просматривается последняя строка симплексной таблицы и в ней отыскивается наибольший положительный элемент.

6 Проверка условия: все a_ir ≤ 0. Если «ДА» - целевая функция неограничена и решения нет, если «НЕТ» - переход к пункту 7. Необходимо проверить элементы разрешающего столбца. Если среди них нет положительных, то задача неразрешима.

7 Выбор разрешающей строки (переменной, выводимой из базиса) по условию:

для a_ir > 0, где s - номер разрешающей строки.

Таким образом, для тех строк, где элементы разрешающего столбца положительны, необходимо найти частное от деления элемента b_i (последний столбец таблицы) на элемент, находящийся в разрешающем столбце. В качестве разрешающей выбирается та строка, для которой результат такого деления будет наименьшим. Элемент, стоящий на пересечении разрешающей строки и разрешающего столбца, называется разрешающим элементом.

8 Пересчет элементов симплекс-таблицы (переход к новому базисному решению).

Для элементов разрешающей строки используются следующие формулы:

где s - номер разрешающей строки, r - номер разрешающего столбца, , - новые значения пересчитываемых элементов, a_sj, b_s - старые значения пересчитываемых элементов, a_sr - старое значение разрешающего элемента. При пересчете элементов разрешающей строки каждый ее элемент делится на разрешающий элемент.

Элементы разрешающего столбца кроме разрешающего элемента, который равен 1, становятся равными нулю: =0,

Элементы, не принадлежащие разрешающим столбцу и строке, пересчитываются по так называемому правилу прямоугольника: мысленно выделяется прямоугольник, в котором элемент, подлежащий пересчету, и разрешающий элемент образуют одну из диагоналей. Формулы будут иметь следующий вид:

где , , , - новые значения пересчитываемых элементов,

a_ij, b_i, c_j, L - старые значения пересчитываемых элементов.

Порядок работы с симплекс таблицей

Первая симплекс-таблица подвергается преобразованию, суть которого заключается в переходе к новому опорному решению.

Правила перехода к следующей таблице:

• просматривается индексная строка (последняя) таблицы и среди коэффициентов этой строки (исключая столбец свободных членов ) выбирается наименьшее отрицательное число при отыскании max, либо наибольшее положительное при решении задачи на min. Если такового нет, то исходное базисное решение является оптимальным и данная таблица является последней;

• просматривается столбец таблицы, отвечающий выбранному отрицательному (положительному) коэффициенту в последней строке- ключевой столбец, и в этом столбце выбираются положительные коэффициенты. Если таковых нет, то целевая функция неограниченна на области допустимых значений переменных и задача решений не имеет;

• среди выбранных коэффициентов столбца выбирается тот, для которого абсолютная величина отношения соответствующего свободного члена (находящегося в столбце свободных членов) к этому элементу минимальна. Этот коэффициент называется разрешающим, а строка в которой он находится ключевой;

• в дальнейшем базисная переменная, отвечающая строке разрешающего элемента, переводится в разряд свободных, а свободная переменная, отвечающая столбцу разрешающего элемента, вводится в число базисных. Строится новая таблица, содержащая новые названия базисных переменных:

• разделим каждый элемент ключевой строки (исключая столбец свободных членов) на разрешающий элемент и полученные значения запишем в строку с измененной базисной переменной новой симплекс таблицы.

• строка разрешающего элемента делится на этот элемент и полученная строка записывается в новую таблицу на то же место.

• в новой таблице все элементы ключевого столбца = 0, кроме разрешающего, он всегда равен 1.

• столбец, у которого в ключевой строке имеется 0,в новой таблице будет таким же.

• строка, у которой в ключевом столбце имеется 0,в новой таблице будет такой же.

• в остальные клетки новой таблицы записывается результат преобразования элементов старой таблицы: новый элемент равен старому элементу минус дробь, в числителе которой стоит произведение элемента текущей строки и разрешающего столбца на элемент разрешающей строки и текущего столбца, а знаменателе – разрешающий элемент.

В результате получают новую симплекс-таблицу, отвечающую новому базисному решению.

Пример расчета по симплекс-методу

На втором листе книги MS Excel получим решение задачи, используя идеи симплекс – метода. Запишем задачу в каноническом виде. Найдем первое допустимое решение. Система ограничений совместна. Ее ранг r=4, следовательно, число свободных переменных k=6-4=2. В качестве свободных выберем х1 и х2, приравниваем их 0, то есть х1=0 и х2=0. Значения базисных неизвестных рассчитываем из системы ограничений. Результаты приведены на рисунке.

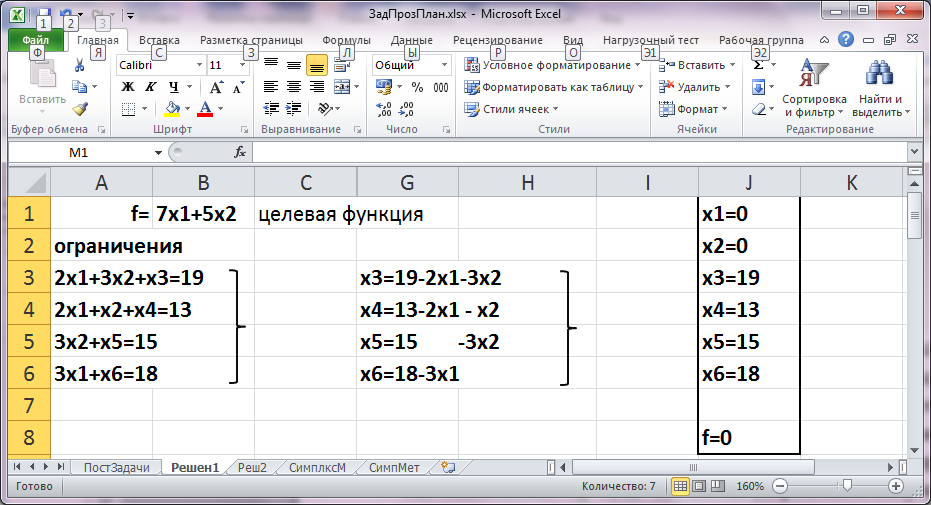
Первое допустимое решение задачи

Значение целевой функции в найденном решении равно 0. Проанализируем, нельзя ли за счет изменения х1 и х2 достигнуть увеличения f. Из записи целевой функции следует, что можно за счет увеличения х1 или х2. Будем увеличивать х1 (х1 входит в целевую функцию с бльшим коэффициентом -7) до тех пор, пока соблюдаются ограничения. Из уравнения x3=19-2x1-3x2 следует, что х1 можно увеличивать до 19/2=9,5, из уравнения x4=13-2x1 - x2 – до 13/2=6,5, из уравнения x5=15-3x2 – до 15/0=∞, из уравнения x6=18-3x1– до 18/3=6. Выбираем минимальное значение х1 равное 6 и переводим х6 в свободные переменные, а х1 – в базис. Пересчитываем систему ограничений, выразив из уравнения x6=18-3x1 х1, и подставив x1=6-1/3x6 в другие уравнения системы ограничений. Результат представлен на рисунке.

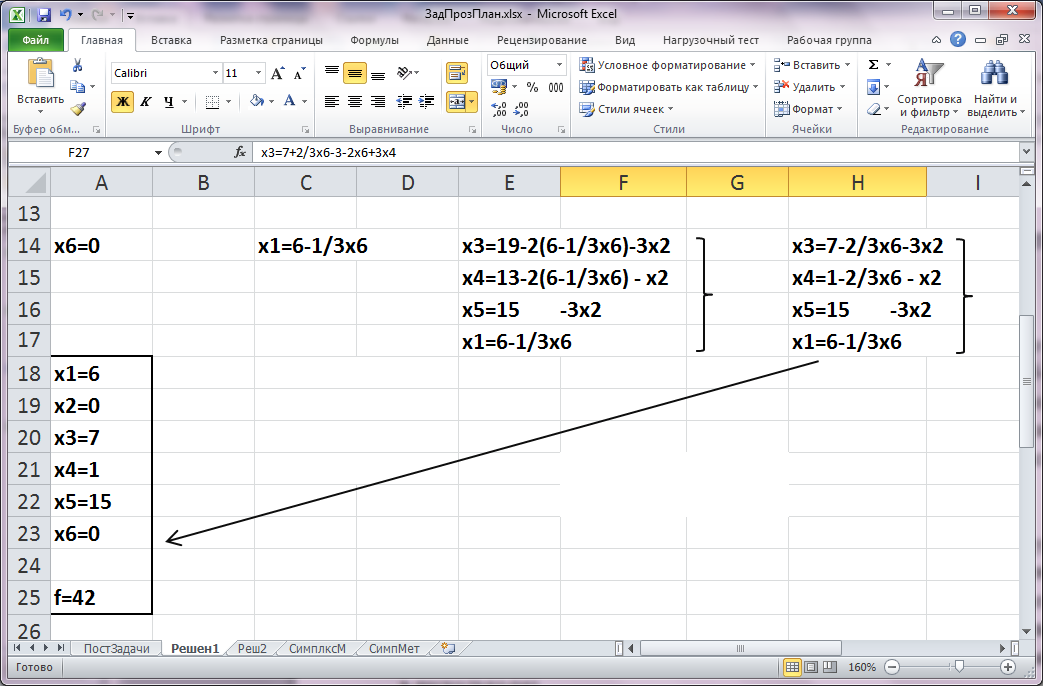
Уточненное допустимое решение задачи

Новое решение лучше предыдущего, так как значение целевой функции увеличилось. Применяя идеи симплекс – метода выполняем последовательно еще два шага для получения оптимального решения.

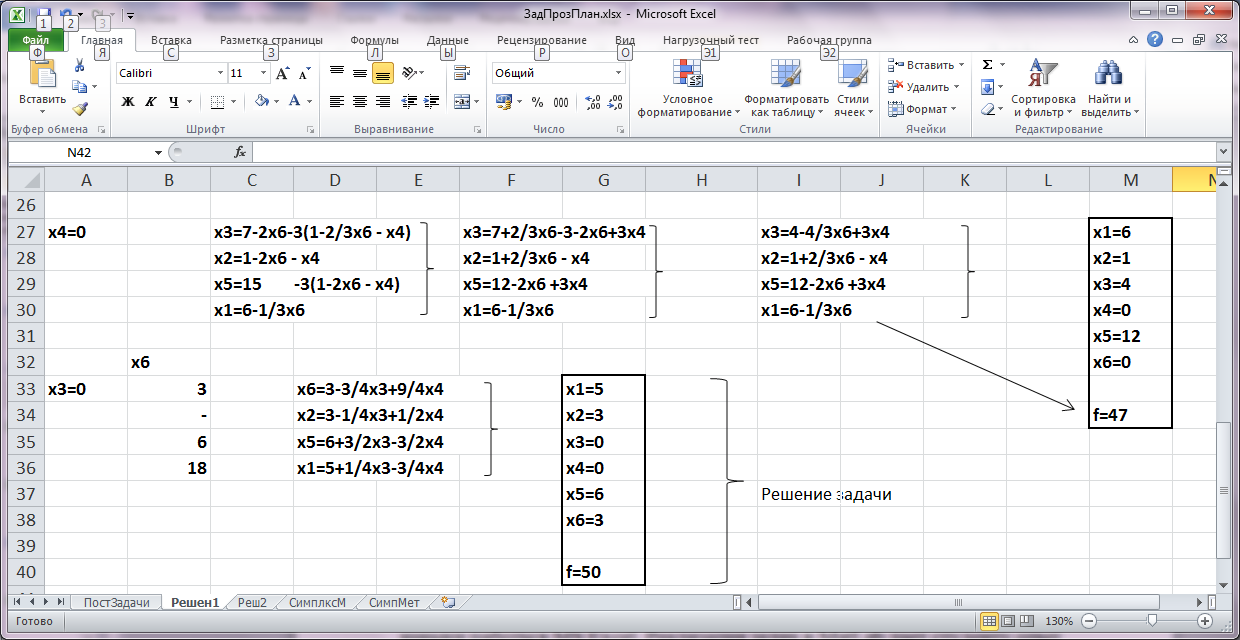
Решение задачи

На третьем листе решим задачу в соответствии с правилами работы с симплекс – таблицами. Симплекс – таблица, соответствующая первому допустимому решению приведена на рисунке.

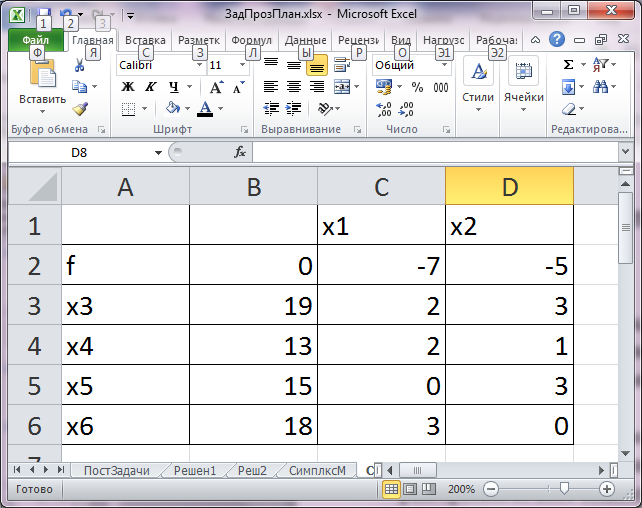
Начальная симплекс – таблица

Выбираем генеральный элемент – α_sr, α_sr=3. Находим =1/α_sr.Заносим его в новую таблицу в клетку, соответствующую генеральному элементу. В новой таблице формируем элементы разрешающей строки по правилу: берем значение из предыдущей таблицы и умножаем на . Элементы разрешающего столбца рассчитываем по правилу: значение из предыдущей таблицы умножаем на -. Остальные клетки заполняем по правилу: из значения предыдущей таблицы вычитаем произведение  на значение из предыдущей таблицы в разрешающей строке и текущем столбце и на значение из предыдущей таблицы в текущей строке и разрешающем столбце. Последовательные симплекс – таблицы расчета показаны на рисунке.

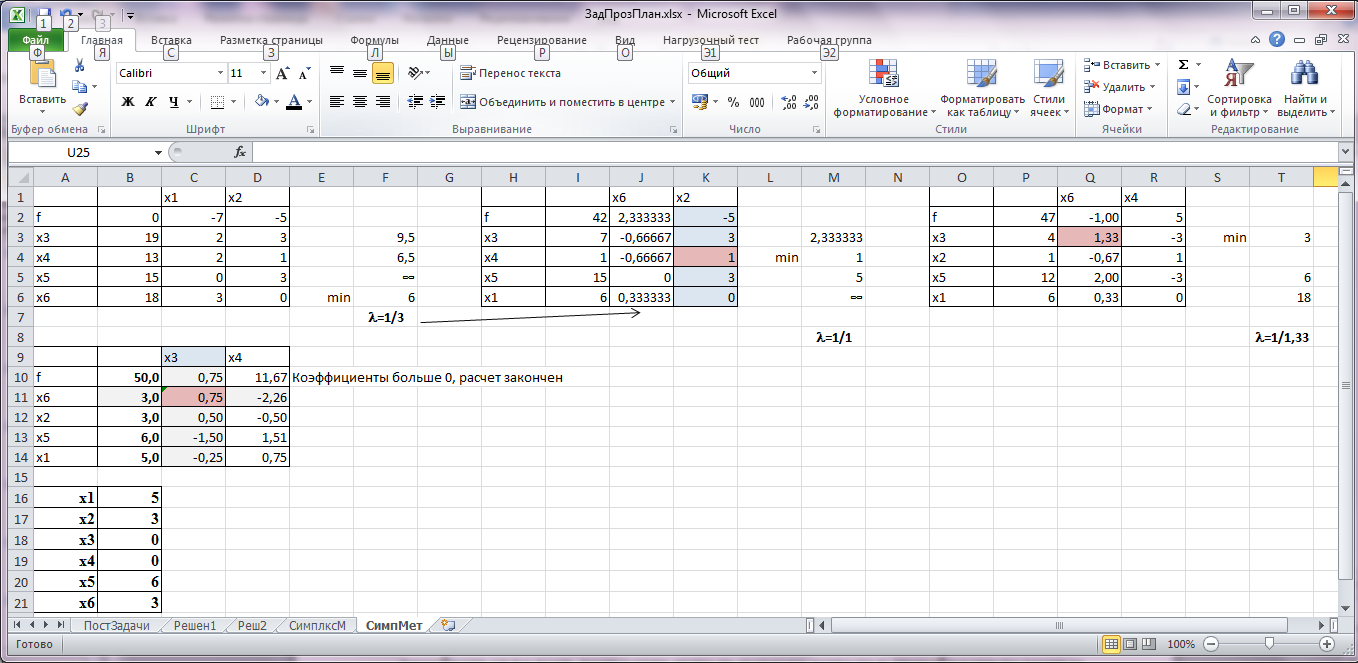
Решение задачи с использованием симплекс – таблиц

На четвертой странице книги MS Excel выполнено решение задачи с помощью функции «Поиск решения».

Заполнение клеток листа MS Excel:

Адрес клетки	Содержание	Тип
A1 - A6	соответствующие надписи с объединением ячеек A1 и A2	Текст
B1 - D2	соответствующие надписи с объединением ячеек B1и B2, C1 и D1	Текст
B7	Доход	Текст
B3 - D6	значения свободных членов и коэффициентов из системы ограничений	Число
C7, D7	значения коэффициентов из целевой функции	Число
G2 - Н3	соответствующие надписи с объединением ячеек G2 и Н2	Текст
G4, Н4	начальные значения х1 и х2 соответственно	Число
E2	Ограничения	Текст
E3	=B3-C3*$G$4-D3*$H$4	Формула
E4: E6	автозаполнение формулой из клетки E3	Формула
G8	Целевая функция	Текст
Н8	=C7*G4+D7*H4	Формула

Рисунок содержит вид листа книги MS Excel перед вызовом функции «Поиск решения».

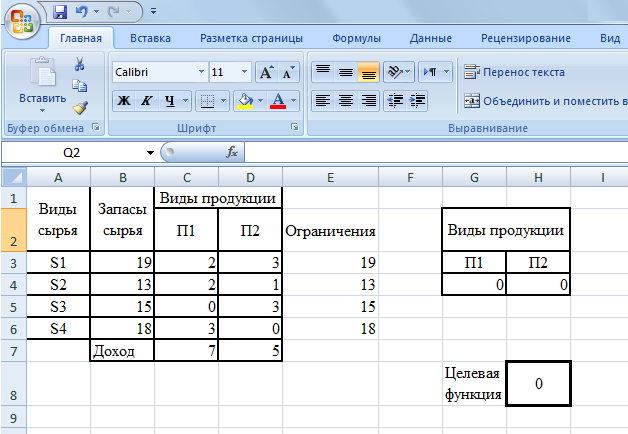
Подготовка к вызову функции «Поиск решения»

На рисунке показан вид диалогового окна функции «Поиск решения».

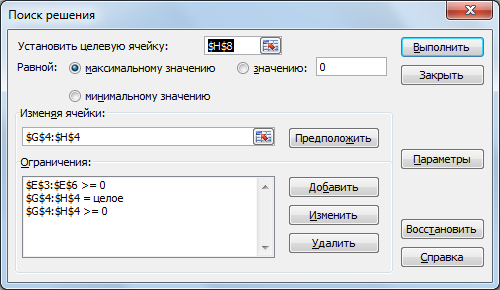
Параметры поиска решения

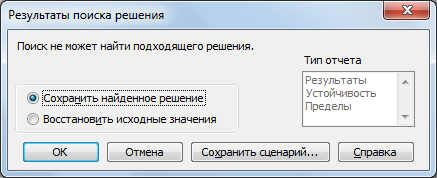
Результаты решения задачи приведены на рисунке.

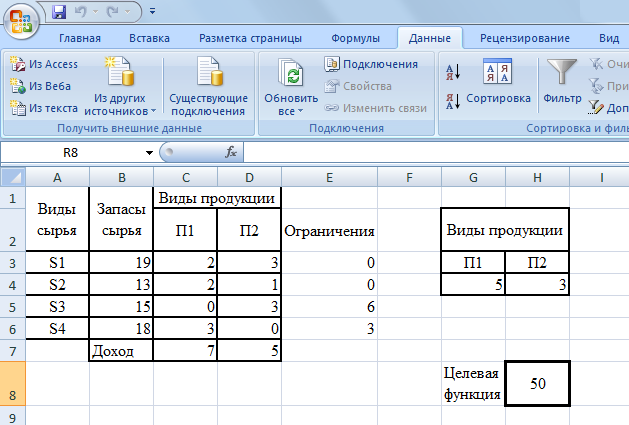
Решение задачи функцией «Поиск решения»

Реализация задачи в MatLab

Функция linprog решает задачу линейного программирования. В MatLab включено несколько вариантов реализации этой функции. Рассмотрим только некоторые из них:

Синтаксис:

x = linprog(f,A,b)

x = linprog(f,A,b,Aeq,beq)

x = linprog(f,A,b,Aeq,beq,lb,ub)

[x,fval] = linprog(...)

Описание:

x = linprog(f,A,b) находит min f'*x при условии, что A*x <= b.

x = linprog(f,A,b,Aeq,beq) решает указанную выше задачу при условии дополнительного выполнения ограничений в виде равенств Aeq*x = beq. Если нет неравенств, то устанавливается A=[] и b=[].

x = linprog(f,A,b,Aeq,beq,lb,ub) определяет набор нижних и верхних границ для проектируемых переменных х, так что решение всегда находится в диапазоне lb <= x <= ub.

[x,fval] = linprog(...) возвращает значение целевой функции fun как решение от х: fval = f'*x.

Рассмотрим использование функции linprog на примере задачи об использовании сырья:

Целевая функция: f=7x₁+5x₂.

Ограничения:

2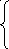x₁+3x₂19

2x₁+ x₂13

3x₂15

3x₁ 19

x₁,x₂0.

Требуется найти максимальное значение целевой функции при заданных ограничениях.

Функция linprog, как было указано выше, находит минимум целевой функции, поэтому приведем целевую функцию к виду f=-7x₁-5x₂, то есть f(х)=-F(х).

В командном окне вводим следующие команды:

>> f=[-7 -5];

>> A=[2 3; 2 1; 0 3; 3 0];

>> b=[19; 13; 15; 18];

>> lb=zeros(2,0);

>> [x, fval]=linprog(f,A,b,[],[],lb,[])

Результаты решения задачи показаны на рисунке:

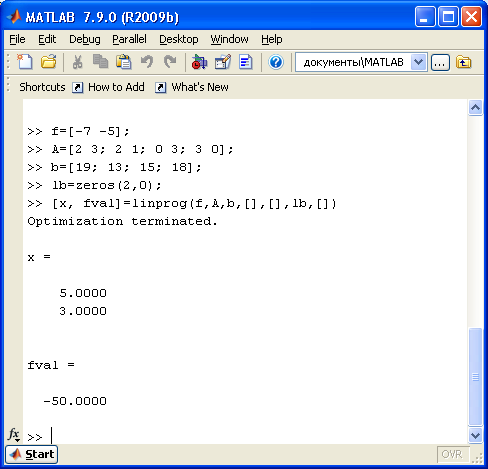
Реализация задачи в MatLab

Ответ: значение целевой функции F=50 (f=-F), при выпуске продукции первого вида 5 единиц и продукции второго вида 3 единицы.