Метод золотого сечения

При построении процесса оптимизации стараются сократить объем вычислений и время поиска. Этого достигают обычно путем сокращения количества вычислений значений целевой функции f(x).Одним из наиболее эффективных методов, в которых при ограниченном количестве вычисленийf(x)достигается наилучшая точность, является метод золотого сечения.

Если известно, что функция f(x)унимодальная на отрезке[a;b], то положение точки минимума можно уточнить, вычисливf(x) в двух внутренних точках отрезка. При этом возможны две ситуации:

	f(x1)<f(x2) минимум находится на отрезке [a, x2].
	f(x1)>f(x2) минимум находится на отрезке [x1, b].

В методе золотого сечения каждая из точек x₁иx₂ делит исходный интервал на две части так, что отношение целого к большей части равно отношении большей части к меньшей, т.е. равно так называемому "золотому отношению". Это соответствует следующему простому геометрическому представлению:

Здесь

или

^{Обозначив , получаем , откуда}

Итак, длины отрезков равны и составляют 0,382от длины интервала(a,b). Соотношением значенийf(x₁) иf(x₂)определяется новый отрезок[a; x₁]или[x_2; b], в котором локализован минимум. Найденный интервал снова делится двумя точками в том же отношении, причем одна из новых точек деления совпадает с уже использованной. Поэтому, начиная со второй итерации, расчет функции необходимо производить только в одной точке, что для сложныхf(x) позволяет существенно сократить время решения задачи.

Алгоритм метода

1. Ввод исходных данных: a, b, ε.

2. Определение положения точек x₁, x₂: x₁=a+0,0,382×(b-a); x₂=a+0,0,618×(b-a).

3. Проверка условия f(x₁) < f(x₂). Если условие выполняется, то b= x₂, иначе a= x₁.

4. Проверка условия (b-a)<= ε. Если условие выполняется, то переход к пункту 5, иначе переход к пункту 2.

5. Расчет закончен. Минимум находится в точке х*=(a+b)/2, минимальное значение функции на отрезке [a;b] равно f(x^*).

Реализация метода золотого сечения в MS Excel

Дано: функция и точность ε=0,01. Найти минимум функции на отрезке [0; 1].

Заполнение клеток листа MS Excel:

Адрес клетки	Содержание	Тип
A1	a	Текст
B1	b	Текст
C1	x1	Текст
D1	x2	Текст
E1	f(x1)	Текст
F1	f(x2)	Текст
G1	b-a	Текст
I1	точность	Текст
J1	0,01	Число
A2	0 - значение a	Число
B2	1 - значение b	Число
C2	=A2+0,318*(B2-A2)	Формула
D2	=A2+0,618*(B2-A2)	Формула
E2	=(0,25*C2+LN(0,5*C2+1)-EXP(-C2*0,75))^2	Формула
F2	=(0,25*D2+LN(0,5*D2+1)-EXP(-D2*0,75))^2	Формула
G2	=B2-A2	Формула
A3	=ЕСЛИ(E2<F2;A2;C2)	Формула
B3	=ЕСЛИ(E2<F2;D2;B2)	Формула
C3	=ЕСЛИ(E2<F2;A3+0,318*(B3-A3);D2)	Формула
D3	=ЕСЛИ(E2<F2;C2;A3+0,618*(B3-A3))	Формула
E3	=ЕСЛИ(E2<F2;(0,25*C3+LN(0,5*C3+1)- EXP(-C3*0,75))^2;F2)	Формула
F3	=ЕСЛИ(E2<F2;E2;(0,25*D3+LN(0,5*D3+1)-EXP(-D3*0,75))^2)	Формула
G3	Автозаполнение формулой из клетки G2	Формула

Первая итерация закончена. Последующие итерации реализуем копированием диапазона ячеек A3: G3 в диапазон ячеек от A4: G4 до A22: G22. Выделим первую строку, где значение (b-a)<= точности. Результат получен за 11 итераций. Итоговые значения запишем в ячейки J4->=( A13+ B13)/2, J5-> =(0,25*J4+LN(0,5*J4+1)-EXP(-J4*0,75))^2.

Вид листа MS Excel:

Ответ:х*=0,813 f(x*)= 0,0 n=11.

Реализация метода в MatLab

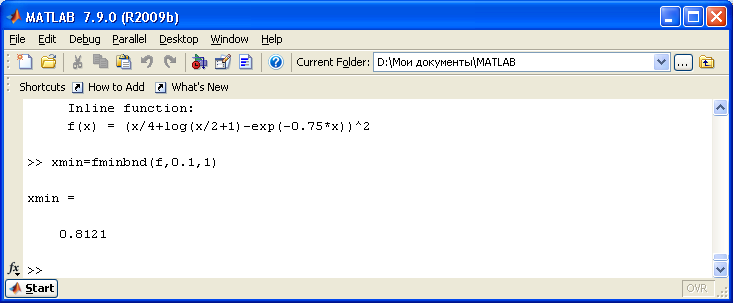
В MatLab вычисление минимума функции одной переменной можно выполнить с помощью функции fminbnd(fun,x1,x2), которая возвращает значение х, являющееся локальным минимумом функции fun(x) на интервале x1<x<x2. Функцию fun(x) зададим, используя функцию inline: f=inline('(x/4+log(x/2+1)-exp(-0,75*x))^2', 'x').

Результаты решения представлены на рисунке: