Метод Рунге-Кутта

Дальнейшее улучшение точности решения ОДУ первого порядка возможно за счет увеличения точности приближенного вычисления интеграла. Воспользовавшись формулой Симпсона, можно получить более точную формулу для решения задачи Коши для ОДУ первого порядка. В формуле Симпсона для приближенного вычисления определенного интеграла используются значения подинтегрального выражения в трех точках. В интеграле их всего две, поэтому введем дополнительную точку в середине отрезка [x_i+1 x_i]

тогда можно переписать так:

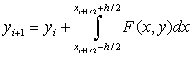
Полученное выражение является неявным, так как в правой части содержатся еще не определенные значения функции y_i+h/2 и y_i+1. Чтобы воспользоваться этой формулой, надо использовать некоторое приближение для вычисления этих значений.

При использовании различных методов приближенного вычисления этих величин, получаются выражения для методов Рунге-Кутта различного порядка точности.

Дано ОДУ вида y'=F(x,y) и начальные условия х₀, у(х₀)=у₀, а так же значение х. Найти у(х).

Классический метод Рунге-Кутта четвертого порядка описывается следующей системой пяти равенств:

y_i+1=y_i+(k₁+2k₂+2k₃+k₄),

где

k₁=F(x_i,y_i),

k₂=F(x_i+,y_i+),

k₃=F(x_i+,y_i+),

k₄=F(x_i+h,y_i+ k₃h).

Строго говоря, существует не один, а группа методов Рунге-Кутта, отличающихся друг от друга порядком, т.е. количеством параметров kj. Рассматриваемый метод четвертого порядка, являющийся одним из наиболее применяемых на практике, обеспечивает достаточно высокую точность и в то же время отличается сравнительной простотой. В большинстве случаев он упоминается в литературе просто как «метод Рунге-Кутта» без указания его порядка.

Алгоритм метода Рунге-Кутта

1. Вводим исходные значенияx₀, y₀, x_n.

2. Задаем значение n, например, 10.

3. Рассчитываем значение h=( x_n- x₀)/n.

4. Последовательно для i=1,2,…,nопределяем:

k₁=F(x_i,y_i), k₂=F(x_i+,y_i+), k₃=F(x_i+,y_i+), k₄=F(x_i+h,y_i+ k₃h),

y_i+1=y_i+(k₁+2k₂+2k₃+k₄).

5. Получаем таблицу значений.

Реализация метода в MS Excel

Дано: , начальные условия y(0)=0,1. Найти у от х=2 при n=10.

Заполнение клеток листа MS Excel для n=10:

Адрес клетки	Содержание	Тип
А1	x0=	Текст
А2	y(x0)=	Текст
B1	0	Число
B2	0,1	Число
D1	n=	Текст
D2	x=	Текст
E1	10	Число
E2	2	Число
G1		Текст
H1	=(E2-B1)/E1	Формула
G2	h/2=	Текст
H2	=H1/2	Формула
A4	x	Текст
B4	x+ h/2	Текст
C4	k1	Текст
D4	k2	Текст
E4	k3	Текст
F4	k4	Текст
G4	y	Текст
A5	=B1	Формула
G5	=B2	Формула
A6	=A5+$H$1	Формула
B6	=A5+$H$2	Формула
C6	=EXP(COS(A5)^2)+1,5*SIN(G5)-2,3/(A5*A5+0,2)	Формула
D6	=EXP(COS(B6)^2)+1,5*SIN(G5+C6*$H$1/2)-2,3/(B6*B6+0,2)	Формула
E6	=EXP(COS(B6)^2)+1,5*SIN(G5+D6*$H$1/2)-2,3/(B6*B6+0,2)	Формула
F6	=EXP(COS(A6)^2)+1,5*SIN(G5+E6*$H$1)-2,3/(A6*A6+0,2)	Текст
G6	=G5+$H$1/6*(C6+2*D6+2*E6+F6)	Текст
A7:A15	Автозаполнение формулой из клетки A6	Формула
B7:B15	Автозаполнение формулой из клетки B6	Формула
C7:C15	Автозаполнение формулой из клетки C6	Формула
D7:D15	Автозаполнение формулой из клетки D6	Формула
E7:E15	Автозаполнение формулой из клетки E6	Формула
F7:F15	Автозаполнение формулой из клетки F6	Формула
G7:G15	Автозаполнение формулой из клетки G6	Формула

Вид листа MS Excel для n=10:

Ответ:х=2 у= -3,172

Результаты расчетов по выше рассмотренным методам приведены на графике:

Реализация задачи в MatLab

В MatLab довольно много функций для решения ОДУ.

В частности функции ode45, ode23,ode133 могут решать системы уравнений явного вида y= F(t, y), а функции ode15s, ode23s, ode23t, ode23tb могут решать как уравнения явного вида, так и уравнения неявного вида F(t, y, y')= 0.

Рассмотрим функцию ode45.

Синтаксис:

[t, X] = ode45('<имя функции>, [t0, tf], x0, tol, trace)

Описание:

Функция ode45 предназначена для численного интегрирования систем ОДУ. Любая система нелинейных ОДУ может быть представлена как система дифференциальных уравнений 1-го порядка в явной форме Коши.

Входные параметры:

<имя функции> - строковая переменная, являющаяся именем m-файла, в котором вычисляются правые части системы ОДУ;

t0 - начальное значение аргумента; tf - конечное значение аргумента;

x0 - начальное значение функции (в точке t0);

tol - задаваемая точность; по умолчанию для ode45 tol = 1.e-6;

trace - флаг, регулирующий вывод промежуточных результатов; по умолчанию равен нулю, что подавляет вывод промежуточных результатов;

Выходные параметры:

t - текущее значение аргумента;

X - двумерный массив, где каждый столбец соответствует одной переменной.

Постановка задачи. Дано: , начальные условия y(0)=0,1. Найти у от х=2.

Решение. В m-файле с именемfunc.mзаписываем подинтегральную функцию:

function d = func( x,y )

d = exp(cos(x).^2)+1.5*sin(y)-2.3/(x.^2+0.2);

end

Вид окна MatLab

В командном окне вызываем функцию ode45, затем функциюplot:

>> [t,z]=ode45('func',[0, 2],0.1);

>> plot(t,z)

Вид командного окна MatLab

Решение задачи в графической форме:

Для получения ответа в командном окне введем следующие команды:

>> k =size(t); ot=[t(k) z(k)]'

Вид командного окна MatLab

Ответ: для конечного значения аргумента равного 2 значение функции равно

-3.172284627552843, что соответствует результатам, полученным в Excel.