Метод трапеций
Графическая интерпретация метода
Разобьем отрезок [a; b] наnравных частей:x0=a, x1=x0+h, x2=x1+h, … , xn=b, где h=(b-a)/n.Площадь всей криволинейной трапеции заменим суммой площадей «маленьких» криволинейных трапеций, образованных при проведении прямыхx=xi. Заменим при вычислении площади каждую «маленькую» криволинейную трапецию прямолинейной трапецией, то есть заменим кривуюf(x) полиномом первой степени – отрезком прямой, соединяющей точкиMi-1{xi-1,f(xi-1)} и Mi{xi,f(xi)}.
Алгоритм метода трапеций
Вводим исходные значения ,a,b.
Задаем n=1, S=0.
Приравниваем S0=S, .n=2·n.
Расчет h=(b-a)/n.
Расчет приближенного значения интеграла:
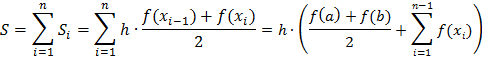
6. Проверка условия |S0-S|<= ε. Если условие выполняется, то переход к пункту 7, иначе переход к пункту 3.
7. Расчет закончен. Результат равен S.
Реализация метода в MS Excel
Вычислить 
dxс точностью=0,001.
Заполнение клеток листа MS Excel для n=2:
|
Адрес клетки |
Содержание |
Тип |
|
A1 |
n=2 |
Текст |
|
A2 |
a= |
Текст |
|
B2 |
0 |
Число |
|
A3 |
b= |
Текст |
|
B3 |
0,5 |
Число |
|
A4 |
h= |
Текст |
|
B4 |
=(B3-B2)/2 |
Формула |
|
A6 |
x |
Текст |
|
B6 |
f |
Текст |
|
A7 |
=B2 |
Формула |
|
B7 |
=EXP(-A7*A7/2) |
Формула |
|
A8 |
=A7+$B$4 |
Формула |
|
B8 |
=EXP(-A8*A8/2) |
Формула |
|
A9 |
=A8+$B$4 |
Формула |
|
B9 |
=EXP(-A9*A9/2) |
Формула |
|
A10 |
S= |
Текст |
|
B10 |
=B4*((B7+B9)/2+B8) |
Формула |
Вид листа MS Excel:
Ответ: 0,4776.
Заполнение клеток листа MS Excel для n=4:
|
Адрес клетки |
Содержание |
Тип |
|
D1 |
n=4 |
Текст |
|
D2 |
a= |
Текст |
|
E2 |
0 |
Число |
|
D3 |
b= |
Текст |
|
E3 |
0,5 |
Число |
|
D4 |
h= |
Текст |
|
E4 |
=(E3-E2)/4 |
Формула |
|
D6 |
x |
Текст |
|
E6 |
f |
Текст |
|
D7 |
=E2 |
Формула |
|
E7 |
=EXP(-D7*D7/2) |
Формула |
|
D8 |
=D7+$E$4 |
Формула |
|
D9:D11 |
Автозаполнение формулой из клетки D8 |
Формула |
|
E8:E11 |
Автозаполнение формулой из клетки Е7 |
Формула |
|
D12 |
S= |
Текст |
|
E12 |
=E4*((E7+E11)/2+СУММ(E8:E10)) |
Формула |
Вид листа MS Excel:
Ответ: 0,47935.
Далее выполняем расчеты для n=8,16.
В клетку H16 вводим формулу=H4*((H7+H15)/2+СУММ(H8:H14)).
Вид листа MS Excel для n=8:
Ответ: 0,479782.
В клетку К24 вводим формулу =K4*((K7+K23)/2+СУММ(K8:K22)).
Вид листа MS Excel для n=16:
Ответ: 0,479889.
Вид таблицы результатов:
Проанализировав значения в этой таблице, увидим, что требуемая точность 0,001 достигнута на второй итерации.
Метод Симпсона (метод парабол)
Графическая интерпретация метода
Разобьем отрезок [a; b] наnравных частей:x0=a, x1=x0+h, x2=x1+h, … , xn=b, где h=(b-a)/n.Площадь всей криволинейной трапеции заменим суммой площадей «маленьких» криволинейных трапеций, образованных при проведении прямыхx=xi. Заменим при вычислении площади каждой «маленькой» криволинейной трапеции кривуюf(x) полиномом второй степени – параболой. Для построения параболы требуется три точки, поэтому будем рассматривать не одну «маленькую» криволинейную трапецию, а две. Следовательно, чтобы каждая «маленькая» криволинейная трапеция, нашла пару необходимо, чтобыnбыло четным. Итак, подынтегральная функцияf(x)заменяется интерполяционным полиномом второй степениP(x)– параболой, проходящей через три узла.
Возьмем три узла x0, x1, x2,через которые проведем параболу, воспользовавшись формулой Ньютона:
Пусть z = x - x0, тогда
Возьмем интеграл по данному интервалу:
.
Для равномерной сетки и четного числа шагов nформула Симпсона принимает вид:
Алгоритм метода Симпсона
Вводим исходные значения ,a,b.
Задаем n=1, S=0.
Приравниваем S0=S, .n=2·n.
Расчет h=(b-a)/n.
Расчет приближенного значения интеграла:
6. Проверка условия |S0-S|<= ε. Если условие выполняется, то переход к пункту 7, иначе переход к пункту 3.
7. Расчет закончен. Результат равен S.
Реализация метода в MS Excel
Вычислить
с
точностью=0,001.
Заполнение клеток листа MS Excel для n=2:
|
Адрес клетки |
Содержание |
Тип |
|
A1 |
n=2 |
Текст |
|
A2 |
a= |
Текст |
|
B2 |
0 |
Число |
|
A3 |
b= |
Текст |
|
B3 |
0,5 |
Число |
|
A4 |
h= |
Текст |
|
B4 |
=(B3-B2)/2 |
Формула |
|
A6 |
x |
Текст |
|
B6 |
f |
Текст |
|
A7 |
=B2 |
Формула |
|
B7 |
=EXP(-A7*A7/2) |
Формула |
|
A8 |
=A7+$B$4 |
Формула |
|
B8 |
=EXP(-A8*A8/2) |
Формула |
|
A9 |
=A8+$B$4 |
Формула |
|
B9 |
=EXP(-A9*A9/2) |
Формула |
|
A10 |
S= |
Текст |
|
B10 |
=B4/3*(B7+4*B8+B9) |
Формула |
Вид листа MS Excel:
Ответ: 0,479952.
Заполнение клеток листа MS Excel для n=4:
|
Адрес клетки |
Содержание |
Тип |
|
D1 |
n=4 |
Текст |
|
D2 |
a= |
Текст |
|
E2 |
0 |
Число |
|
D3 |
b= |
Текст |
|
E3 |
0,5 |
Число |
|
D4 |
h= |
Текст |
|
E4 |
=(E3-E2)/4 |
Формула |
|
D6 |
x |
Текст |
|
E6 |
f |
Текст |
|
D7 |
=E2 |
Формула |
|
E7 |
=EXP(-D7*D7/2) |
Формула |
|
D8 |
=D7+$E$4 |
Формула |
|
D9:D11 |
Автозаполнение формулой из клетки D8 |
Формула |
|
E8:E11 |
Автозаполнение формулой из клетки Е7 |
Формула |
|
D12 |
S= |
Текст |
|
E12 |
=E4/3*(E7+E11+4*(E8+E10)+2*E9) |
Формула |
Вид листа MS Excel:
Ответ: 0,479927.
Далее выполняем расчеты для n=8,16.
В клетку H16 вводим формулу=H4/3*(H7+H15+4*(H8+H10+H12+H14)+2*(H9+H11+H13)).
Вид листа MS Excel для n=8:
Ответ: 0,479925.
В клетку К24 вводим формулу
=K4/3*(K7+K23+4*(K8+K10+K12+K14+K16+K18+K20+K22)+2*(K9+K11+K13+ K15+K17+K19+K21))
Вид листа MS Excel для n=16:
Ответ: 0,479925.
Вид таблицы результатов:
Проанализировав значения в этой таблице, увидим, что требуемая точность 0,001 достигнута сразу после первой итерации.
Реализация символьного вычисления неопределенного интегралав MatLab
Символьные вычисления неопределенных интегралов в MatLabосуществляется при помощи функции:int(fun, var), гдеfun– символьное выражение, представляющее собой подынтегральную функцию, аvar – переменная интегрирования.
Пример 1.
Постановка задачи. Вычислить неопределенный интеграл
Решение. В командном окне введем следующие команды:
syms x %Определение символьной переменной
f=sym('sin(x)') ; %Определение символьной функции
int(f,x) %Вычисление неопределенного интеграла
Вид окна MatLab
Пример 2.
Постановка задачи. Вычислить неопределенный интеграл
Решение. В командном окне введем следующие команды:
syms x %Определение символьной переменной
f=sym('exp(-x*x/2)') ; %Определение символьной функции
int(f,x) %Вычисление неопределенного интеграла
Вид окна MatLab
Функция ошибки erf(x)определяется следующим образом:
Реализация вычисления определенного интегралав MatLab
Вычислительный алгоритм метода Симпсона с автоматическим выбором шага реализован функцией quad(name, a, b [,eps, trace]), где
name– имя М-функции, задающей подынтегральное выражение;
a, b– пределы интегрирования;
eps– точность вычисления (необязательный параметр);
trace– параметр, позволяющий получить информацию о ходе вычислений в виде таблицы, в столбцах представлены значение количества вычислений, начальная точка текущего промежутка интегрирования, его длина и значение интеграла (необязательный параметр).
Пример 1
Постановка задачи. Вычислить определенный интеграл
с
точностью 1е-5.
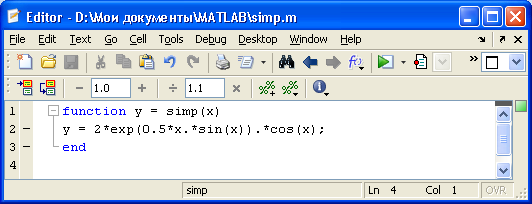
Решение. В m-файле с именемsimp.mзаписываем подинтегральную функцию:
function y=simp(x)
y = 2*exp(0.5*x.*sin(x)).*cos(x);
end
Вид окна MatLab
В командном окне вызываем функцию quad:
quad('simp',1,1.5,1.0e-05)
Вид командного окна MatLab
Пример 2
Постановка задачи. Вычислить определенный интеграл
с
точностью 1е-3.
Решение. В m-файле с именемsimp.mзаписываем подинтегральную функцию:
function y=simp(x)
y = 2*exp(0.5*x.*sin(x)).*cos(x);
end
Вид окна MatLab
В командном окне вызываем функцию quad:
quad('simp',0,0.5,1.0e-07)
Вид командного окна MatLab
Ответ: 0,47992521, что соответствует результатам, полученным в Excel.