Полиномиальная (алгебраическая) интерполяция

Если в качестве интерполяционной функции выбран многочлен от од ой переменной: P(x)=a₀ + a₁·x + a₂·x² + a₃·x³ +…+a_n·xⁿ, такая интерполяция называется алгебраической интерполяцией. В этом случае СЛАУ для определения коэффициентов интерполяционного полинома имеет вид:

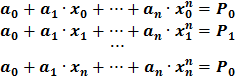
а ее определитель:

отличен от нуля, так как узлы интерполяции попарно различны. Это известный из курса линейной алгебры определитель Вандермонда. Следовательно, решение задачи алгебраической интерполяции всегда существует и единственно.

Прямое решение этой системы никогда не используется в практических вычислениях. При больших nсистема для определения коэффициентов интерполяции оказывается плохо обусловленной. Однако решение этой задачи можно построить другим способом:

Такой вид записи алгебраического интерполяционного полинома называется интерполяционным полиномом в форме Лагранжа. Он удобен для теоретического рассмотрения, но на практике часто оказывается более удобной другая форма представления — полином в форме Ньютона.

Интерполяционный полином в форме Ньютона

Пусть задана табличная функция. Построим таблицу разделенных разностей

	fn	f(xn-1,xn)	f(xn-2,xn-1,xn)	f(x0,x1,…,xn)

^{Введем обозначениеi≠j, разделенная разность (или разностноеотношение) первого порядка. Очевидно, что.}

Вычислим все разностные отношения первого порядка по двум первым точкам (разделенные разности). Определим рекуррентно разделенные разности более высокого порядка.

Теперь можно построить всю таблицу разделенных разностей.

Предположим, что сетка равномерная, т.е. x_k=x₀+kh.

Если мы вычислим вторую производную в точке x₁:

Разделенная разность второго порядка, то она будет аппроксимировать производную второго порядка с точностью до числового множителя 0,5. Если аналогично рассуждать дальше, то разделенная разность порядка kбудет аппроксимировать соответствующую производную с точностью до числового множителя 1/k!.

По данным на сетке наибольший порядок разности, которую возможно вычислить f(x₀, x₁, … ,x_n) - разделенная разностьn-ого порядка.

Определим Pⁿ(x)=f₀+f(x₀,x₁)·(x-x₀)+ f(x₀,x₁,x₂)·(x-x₀)·(x-x₁)+…+ f(x₀,x₁,...,x_n)·(x-x₀) ·(x-x₁) ·…·(x-x_n-1).

Это и есть интерполяционный полином в форме Ньютона. Проверим, что этот полином является интерполяционным. Применим метод математической индукции. Надо проверить совпадения интерполяционного полинома и функции в узлах интерполяции.

x=x₀, P(x₀)=f₀,

^x=x₁^{, P}₁ ^{= и так далее.}

Интерполяция по Лагранжу

^{Пусть некоторая функция y=f(x) задана таблично:}

xi	yi
x0	y0
x1	y1
.	.
.	.
.	.
xn	yn

где x₀, x₁,..., x_n- узлы интерполяции.

Найти интерполяционный многочлен Лагранжа L_n(x)и вычислить значение функцииf(x)в точкес, несовпадающей ни с одним из узлов интерполяции.

Многочлен Лагранжа, как это было рассмотрено выше, строят следующим образом:

Эту формулу можно записать несколько иначе:

Обозначим , а z_i=

Тогда . Запишемв видеи будем вычислять коэффициенты,, … ,

Для n=1

i=0 s₀=, a₀₀=-x₁, a₀₁=1; i=1 s₁=, a₁₀=-x₀, a₁₁=1.

Для n=2

i=0 s₀=, a₀₀=x₁·x₂, a₀₁=-(x₁+x₂), a₀₂=1;

i=1 s₁=, a₁₀=x₀·x₂, a₁₁=-(x₀+x₂), a₁₂=1;

i=2 s₂=, a₂₀=x₀·x₁, a₂₁=-(x₀+x₁), a₂₂=1.

Для n=3

i=0 s₀=, a₀₀=-x₁·x₂·x₃, a₀₁=(x₁·x₂+ x₁·x₃+ x₂·x₃),

a₀₂=-(x₁+x₂+x₃), a₀₃=1;

i=1 s₁=, a₁₀=-x₀·x₂·x₃, a₁₁=(x₀·x₂+ x₀·x₃+ x₂·x₃),

a₁₂=-(x₀+x₂+x₃), a₁₃=1;

i=2 s₂=, a₂₀=-x₀·x₁·x₃, a₂₁=(x₀·x₁+ x₀·x₃+ x₁·x₃),

a₂₂=-(x₀+x₁+x₃), a₂₃=1;

i=3 s₃=, a₃₀=-x₀·x₁·x₂, a₃₁=(x₀·x₁+ x₀·x₂+ x₁·x₂),

a₃₂=-(x₀+x₁+x₂), a₃₃=1.

Аналогичным образом можно найти коэффициенты для любого значения n.

Алгоритм метода

1. Ввод исходных данных: таблицы значений x_i,y_i, i=0,1,2,..,n и с.

2. Расчет значений s_i.

3. Расчет коэффициентов a_ij.

4. Расчет L_i.

5. Расчет L_n=.

6. Расчет L_n(с).

7. Вывод результатов.

Реализация метода в MS Excel

Исходные данные для расчета:

x	y
0	2,218282
1	1,216526
2	0,159583
3	-0,12842
4	0,020147
5	0,827984

Заполнение клеток листа MS Excel:

Адрес клетки	Содержание	Тип
A2	x	Текст
B2	y	Текст
A3:B8	Исходные данные	Число
A10	c равное 1,5	Число
D2	yi/П(xi-xj)	Текст
K2:F2	а5i а4i а3i а2i а1i а0i соответственно	Текст
N2:R2	x5 x4 x3 x2 x соответственно	Текст
D3	=B3/((A3-A4)*(A3-A5)*(A3-A6)*(A3-A7)* (A3-A8))	Формула
D4	=B4/((A4-A5)*(A4-A6)*(A4-A7)*(A4-A8)* (A4-A3))	Формула
D5	=B5/((A5-A6)*(A5-A7)*(A5-A8)*(A5-A4)* (A5-A3))	Формула
D6	=B6/((A6-A7)*(A6-A8)*(A6-A3)*(A6-A4)* (A6-A5))	Формула
D7	=B7/((A7-A8)*(A7-A3)*(A7-A4)*(A7-A5)* (A7-A6))	Формула
D8	=B8/((A8-A3)*(A8-A4)*(A8-A5)*(A8-A6)* (A8-A7))	Формула
F3:F8	1	Число
G3	=-(A$4+A$5+A$6+A$7+A$8)	Формула
G4	=-(A$3+A$5+A$6+A$7+A$8)	Формула
G5	=-(A$3+A$4+A$6+A$7+A$8)	Формула
G6	=-(A$3+A$4+A$5+A$7+A$8)	Формула
G7	=-(A$3+A$4+A$5+A$6+A$8)	Формула
G8	=-(A$3+A$4+A$5+A$6+A$7)	Формула
H3	=(A4*A5+A4*A6+A4*A7+A4*A8+A5*A6+ A5*A7+A5*A8+A6*A7+A6*A8+A7*A8)	Формула
H4	=(A5*A3+A5*A6+A5*A7+A5*A8+A6*A7+ A6*A8+A6*A3+A7*A8+A7*A3+A8*A3)	Формула
H5	=(A6*A7+A6*A8+A6*A3+A6*A4+A7*A8+ A7*A3+A7*A4+A8*A3+A8*A4+A3*A4)	Формула
H6	=(A7*A8+A7*A3+A7*A4+A7*A5+A8*A3+ A8*A4+A8*A5+A3*A4+A3*A5+A4*A5)	Формула
H7	=(A8*A3+A8*A4+A8*A5+A8*A6+A3*A4+ A3*A5+A3*A6+A4*A5+A4*A6+A5*A6)	Формула
H8	=(A3*A4+A3*A5+A3*A6+A3*A7+A4*A5+ A4*A7+A4*A6+A5*A6+A5*A7+A6*A7)	Формула
I3	=-(A4*A5*A6+A4*A5*A7+A4*A5*A8+ A4*A6*A7+A4*A6*A8+A4*A7*A8+A5*A6*A7+A5*A6*A8+A5*A7*A8+A6*A7*A8)	Формула
I4	=-(A5*A6*A7+A5*A6*A8+A5*A6*A3+ A5*A7*A8+A5*A7*A3+A5*A8*A3+A6*A7*A8+A6*A7*A3+A6*A8*A3+A7*A8*A3)	Формула
I5	=-(A6*A7*A8+A6*A7*A3+A6*A7*A4+ A6*A8*A3+A6*A8*A4+A6*A3*A4+A7*A8*A3+A7*A8*A4+A7*A3*A4+A8*A3*A4)	Формула
I6	=-(A7*A8*A3+A7*A8*A4+A7*A8*A5+ A7*A3*A4+A7*A3*A5+A7*A4*A5+A8*A3*A4+A8*A3*A5+A8*A4*A5+A3*A4*A5)	Формула
I7	=-(A8*A3*A4+A8*A3*A5+A8*A3*A6+ A8*A4*A5+A8*A4*A6+A8*A5*A6+A3*A4*A5+A3*A4*A6+A3*A5*A6+A4*A5*A6)	Формула
I8	=-(A3*A4*A5+A3*A4*A6+A3*A4*A7+ A3*A5*A6+A3*A5*A7+A3*A6*A7+A4*A5*A6+A4*A5*A7+A4*A6*A7+A5*A6*A7)	Формула
J3	=A4*A5*A6*A7+A4*A5*A6*A8+A4*A5*A7*A8+A4*A6*A7*A8+A5*A6*A7*A8	Формула
J4	=A5*A6*A7*A8+A5*A6*A7*A3+A5*A6*A8*A3+A5*A7*A8*A3+A6*A7*A8*A3	Формула
J5	=A6*A7*A8*A3+A6*A7*A8*A4+A6*A7*A3*A4+A6*A8*A3*A4+A7*A8*A3*A4	Формула
J6	=A7*A8*A3*A4+A7*A8*A3*A5+A7*A8*A4*A5+A7*A3*A4*A5+A8*A3*A4*A5	Формула
J7	=A8*A3*A4*A5+A8*A3*A4*A6+A8*A3*A5*A6+A8*A4*A5*A6+A3*A4*A5*A6	Формула
J8	=A3*A4*A5*A6+A3*A4*A5*A7+A3*A4*A6*A7+A3*A5*A6*A7+A4*A5*A6*A7	Формула
K3	=-A4*A5*A6*A7*A8	Формула
K4	=-A5*A6*A7*A8*A3	Формула
K5	=-A6*A7*A8*A3*A4	Формула
K6	=-A7*A8*A3*A4*A5	Формула
K7	=-A8*A3*A4*A5*A6	Формула
K8	=-A3*A4*A5*A6*A7	Формула
N3	=F3*$D3	Формула
N4	=F4*$D4	Формула
N5	=F5*$D5	Формула
N6	=F6*$D6	Формула
N7	=F7*$D7	Формула
N8	=F8*$D8	Формула
O3	=G3*$D3	Формула
O4	=G4*$D4	Формула
O5	=G5*$D5	Формула
O6	=G6*$D6	Формула
O7	=G7*$D7	Формула
O8	=G8*$D8	Формула
P3	=H3*$D3	Формула
P4	=H4*$D4	Формула
P5	=H5*$D5	Формула
P6	=H6*$D6	Формула
P7	=H7*$D7	Формула
P8	=H8*$D8	Формула
Q3	=I3*$D3	Формула
Q4	=I4*$D4	Формула
Q5	=I5*$D5	Формула
Q6	=I6*$D6	Формула
Q7	=I7*$D7	Формула
Q8	=I8*$D8	Формула
R3	=J3*$D3	Формула
R4	=J4*$D4	Формула
R5	=J5*$D5	Формула
R6	=J6*$D6	Формула
R7	=J7*$D7	Формула
R8	=J8*$D8	Формула
S3	=K3*$D3	Формула
S4	=K4*$D4	Формула
S5	=K5*$D5	Формула
S6	=K6*$D6	Формула
S7	=K7*$D7	Формула
S8	=K8*$D8	Формула
M10	аj	Текст
N10	=СУММ(N3:N8)	Формула
O10: S10	Автозаполнение формулой из N10	Формула
B10	=N9*A10^5+O9*A10^4+P9*A10^3+Q9*A10^2+ R9*A10+S9	Формула

Вид листа MS Excel.

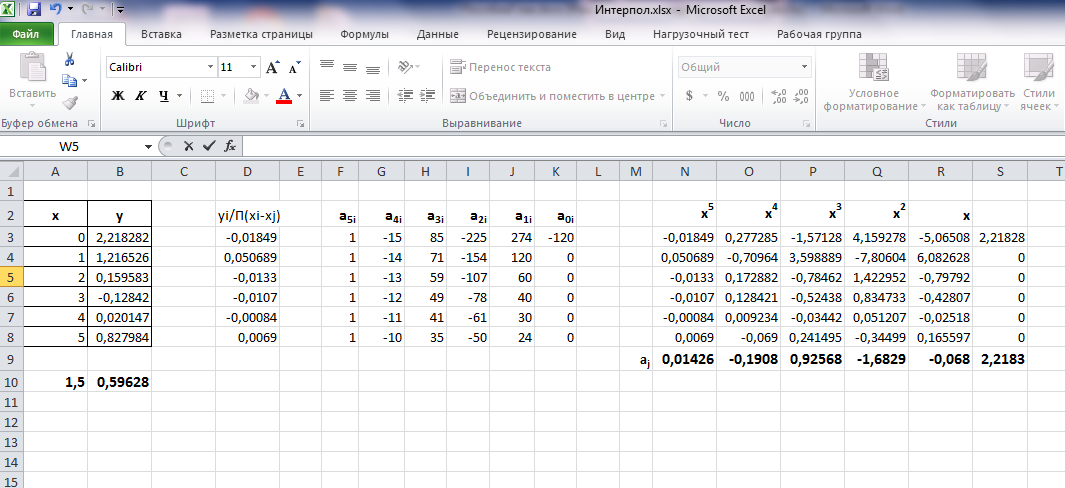
Ответ: Интерполяционная функция 0,01426·х⁵-0,1908·х⁴+0,92568·х³-1,6829·х²-0,068·х+2,2183 и значение функции в точке с=1,5 равно 0,59628.

Реализация в MatLab

Дано: таблица значений функции

x	y
0	2,218282
1	1,216526
2	0,159583
3	-0,12842
4	0,020147
5	0,827984

точка с=1,5.

Найти значение функции в точке с (задача уплотнения таблицы) по методу Лагранжа.

Решение. Воспользуемся интерполяционной формулой Лагранжа

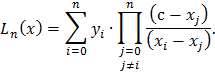Составим функцию, реализующую расчет по этой формуле.

function L = lagrang(x,y,c)

% вычисление интерполяционного полинома в форме Лагранжа

% x - массив координат узлов

% y - массив значений интерполируемой функции

% c - значение аргумента, для которого надо вычислить значение функции

% L - значение функции в точке с

% число узлов интерполяции

N=length(x);

% обнуляем L

L=0;

for k=1:N

t=1;

for j=[1:k-1,k+1:N]

t=t*(с-x(j))/(x(k)-x(j));

end

L=L+y(k)*t;

end

end

Сохраним эту функции в файле lagrang.m.

Реализация функции в MatLab:

В командном окне введем следующие команды:

% Задаем значения х

>> x=0:1:5;

% Задаем значения у

>> y=[2.218282 1.216526 0.159583 -0.12842 0.020147 0.827984];

% Задаем значение с

>> с=1.5;

>> L=lagrang(x,y,с);

Реализация в MatLab:

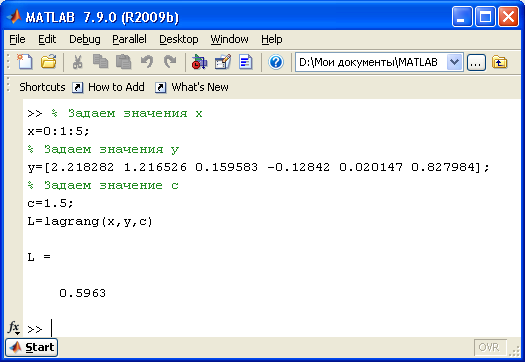
Пример. Постановка задачи. Прямой расчет по функции Лапласа достаточно сложен, поэтому практически во всех книгах по теории вероятности и математической статистике приводятся таблицы значений этой функции. Возьмем часть одной из таких таблиц в качестве исходных данных:

x	y
0,1	0,0398
0,15	0,0596
0,2	0,0793
0,25	0,0987
0,3	0,1179
0,35	0,1368

Найти интерполяционную функцию по методу Лагранжа и рассчитать значение функции в точке 0,22.

Решение задачи средствами MS Excel

Скопируем диапазон клеток A2:S10 с листа MS Excel с предыдущим расчетом и вставим на новый лист в клетки A6:S14. В клетки A7: B12 введем исходные данные и получим коэффициенты интерполяционной функции. В клетку А14 запишем значение 0,22 и клетке В14 увидим значение у (0,22). Найдем расчетное значение функции Лапласа по формуле и запишем в клетку В15.

Вид листа MS Excel.

Ответ: Интерполяционная функция -13,33·х⁵+15,333·х⁴-6,833·х³+1,4217·х²+0,2582·х+0,005 и значение функции в точке с=0,22 равно 0,08709, которое хорошо согласуется с значением по формуле Лапласа.

Решение задачи в MatLab

Решение рассматриваемого примера показано на рисунке:

Ответ: значение функции в точке 0,22 равно 0,0871.