Метод Гаусса - Зейделя

Постановка задачи, достаточное условие сходимости и выбор начального приближения в методе Гаусса – Зейделя такие же, как и в методе простой итерации.

Описание метода Гаусса - Зейделя

Как и в методе простой итерации из первого уравнения системы

a₁₁·x₁ +a₁₂·x₂+…+a_1n·x_n=b₁

a₂₁·x₁ +a₂₂·x₂+…+a_2n·x_n=b₂

……

a_n1·x₁ +a_n2·x₂+…+a_nn·x_n=b_n

выражаем х₁, из второго – х₂ и так далее. Получим:

x₁= b₁/a₁₁ – (a₁₂·x₂+ a₁₃·x₃+…+a_1n·x_n)/ a₁₁

x₂= b₂/a₂₂ – (a₂₁·x₁+ a₂₃·x₃+…+a_2n·x_n)/ a₂₂

_……..

x_j= b_j /a_jj – (a_j1·x₁+ a_j2·x₂+…+a_jj-1·x_j-1+a_jj+1·x_j+1+…+a_jn·x_n)/ a_jj

_……..

x_n= b_n /a_nn – (a_n1·x₁+ a_n2·x₂+…+a_nn-1·x_n-1)/ a_nn

Начало любой новой итерации начинается с расчета х₁. К этому моменту известны значения с предыдущей итерации, поэтому формула для такая же, как и в методе простой итерации: . Различия метода Гаусса – Зейделя начинаются с расчета . В правой части формулы для х₁ используется значение, полученное на данной итерации, а не с предыдущей, как в методе простой итерации:

.

При расчетах , и так далее в правых частях формул используются значения х, найденные на текущей итерации:

Алгоритм метода

1. Ввод исходных данных: А, b, .

2. Задание начального приближения .

3. Присваиваем .

4. Расчет . Расчетная формула:

5. Вычисляем наибольшую из разностей ||.

6. Проверяем условие max||Если оно выполняется, то переход к пункту 7, иначе переход к новой итерации к пункту 3.

7. Расчет закончен. Результат – значения

Реализация метода в MS Excel

Рассмотрим реализацию того же примера, что и для метода простой итерации.

Заполнение клеток листа MS Excel:

Адрес клетки	Содержание	Тип
A3:A5	j=	Текст
C1:E1	i=	Текст
B2	aij	Текст
B3:B5	Арифметическая последовательность 1,2,3	Число
C2:E2	Арифметическая последовательность 1,2,3	Число
F2	b	Текст
H1:J1	Начальное приближение	Текст
H2:J2	Арифметическая последовательность 1,2,3	Число
C3:E5	Коэффициенты при неизвестных - матрица A	Число
F3:F5	Значения правых частей - b	Число
H3	=F3/C3	Формула
I3	=F4/D4	Формула
J3	=F5/E5	Формула
C7:I7	x01 x02 x03 x11 x12 x13 max(x1-x0)	Текст
A9:A22	Итерация	Текст
B9:B22	Арифметическая последовательность 1,2,3, …,14	Число
C9	=H3	Формула
D9	=I3	Формула
E9	=J3	Формула
F9	=$F$3/$C$3-($D$3*D9+$E$3*E9)/$C$3	Формула
G9	=$F$4/$D$4-($C$4*F9 +$E$4*E9)/$D$4	Формула
H9	=$F$5/$E$5-($C$5*F9+$D$5*G9)/$E$5	Формула
I9	=МАКС(ABS(F9-C9);ABS(G9-D9);ABS(H9-E9))	Формула
C10	=F9	Формула
D10	=G9	Формула
E10	=H9	Формула
F10:I10	Копирование диапазона F9:I9	Формула
C11:I11 и далее	Копирование диапазона C10:I10	Формула

Формулы, в которых есть отличия, выделены полужирным шрифтом.

Замечание. Можно с листа, на котором реализован метод простой итерации, скопировать диапазон клеток A1:J19 и изменить формулы в клетках G9 и H9 в соответствии с алгоритмом метода Гаусса - Зейделя. Затем копируем диапазонF9:I9 на десятую строку. Выделяем диапазонC10:I10 и выполняем автозаполнение до девятнадцатой строки.

Вид листа MS Excel.

Проанализировав полученные значения увидим, что требуемая точность достигнута на шестой итерации, что значительно лучше, чем в методе простой итерации.

Ответ: х* ={ 1; 1; 1}

Пример. Постановка задачи.Дано СЛАУ:

1,53·х₁ – 1,63·х₂ – 0,76·х₃ = 2,18

0,86·х₁ + 1,17·х₂ + 1,84·х₃ = 1,95

0,32·х₁ – 0,65х₂ + 1,11·х₃ = -0,47

и точность =0,0001. Найти решение этой системы двумя методами: простой итерации и методом Гаусса – Зейделя.

Система имеет единственное решение, так как определитель системы равен 5,12.

Условие сходимости i=1,2,3, не выполняется. Выполним равносильные преобразования:

• сложим первое и второе уравнения: 2,39·х₁ – 0,46·х₂ + 1,08·х₃ = 4,13;

• вычтем из второго уравнения третье: 0,54·х₁ + 1,82·х₂ + 0,73·х₃ = 2,42;

• сложим второе и третье уравнения: 1,18·х₁ + 0,52·х₂ + 2,95·х₃ = 1,48.

Действительно, условия сходимости для преобразованной системы выполняются |2,39|>|-0,46|+|1,08|; |1,82|>|0,54|+|0,73|; |2,95|>|1,18|+|0,52|.

Итак, решаем преобразованную систему:

2,39·х₁ – 0,46·х₂ + 1,08·х₃ = 4,13

0,54·х₁ + 1,82·х₂ + 0,73·х₃ = 2,42

1,18·х₁ + 0,52·х₂ + 2,95·х₃ = 1,48.

Реализация метода простой итерации. Вид листа MS Excel.

Реализация метода Гаусса - Зейделя. Вид листа MS Excel.

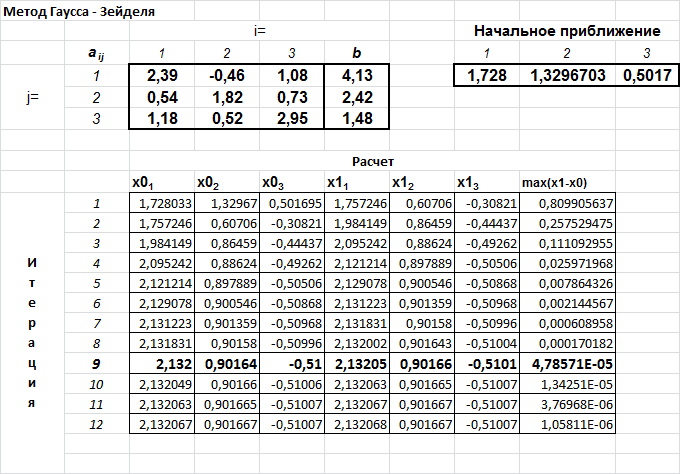
Результаты расчетов приведены в таблице:

Метод простой итерации	Метод Гаусса - Зейделя
x*={2,1302; 0,901684; -0,51001} достигнутая точность 8,5·10-5 число итераций 12	x*={2,132054; 0,90166; -0,5101} достигнутая точность 4,8·10-5 число итераций 9

Реализация решения задачи в MatLab

Методы решения СЛАУ в MatLabоснованы на использовании матричной формы записи: AX = B.