§2. Дифракция Фраунгофера на прямоугольной щели

Ключевые понятия:

• параметр дифракции,

• ближняя зона,

• дальняя зона,

• дифракция Фраунгофера,

• дифракционная расходимость.

3

.2.1. ПАРАМЕТР ДИФРАКЦИИ. БЛИЖНЯЯ И ДАЛЬНЯЯ ЗОНЫ ДИФРАКЦИИ. В общем случае дифракционное препятствие может иметь любую форму: отверстие, диск, щель, проволока и т. д. Для анализа характера дифракции удобно использовать число зон Френеля, которое для плоских волн равно

Тогда выделяются характерные зоны:

• Дифракция не наблюдается и выполняются законы геометрической оптики, если

• Н

  m 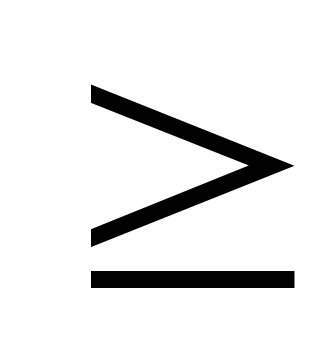1.

  m >>1.

  аблюдается дифракция Френеля (ближняя зона), если.

^{В ближней зоне интенсивность света} на оси пучка практически постоянна и равна ^{интенсивности исходной световой волны. Пучок сохраняет пространственную структуру, заданную} формой отверстия^{. В пределах отверстия помещается порядка 50} зон ^{Френеля.}

• Наблюдается дифракция Фраунгофера (дальняя зона), если

В

m < 1.

дальней зоне интенсивность света на оси пучка много меньше интенсивности исходной волны и с увеличением расстояния уменьшается обратно пропорционально квадрату рассто-яния. Световой пучок расширяется. В пределах отверстия помещается только малая центральная часть первой зоны Френеля. Характер изменения интенсивности света I  на оси отверстия с ростом увеличения расстояния от экрана  b при неизменном радиусе отверстия приводится на рисунке. По мере удаления от экрана периферийные зоны Френеля одна за другой начнут выходить за пределы отверстия, пока, наконец, в пределах отверстия не остается одна первая зона Френеля. В этот момент интенсивность света I в точке наблюдения достигает максимума, после чего монотонно убывает с ростом расстояния b. Расстояние Zg, при котором отверстие совпадает с первой зоной Френеля, называют дифракционной длиной светового пучка. Дифракционная длина определяет границу между ближней и дальней зонами дифракции:

3.2.2. ДИФРАКЦИЯ ФРАУНГОФЕРА.Дифракция Фраунгофера наблюдается, если на препятствие падает плоская волна и точка наблюдения удалена на расстояние, большее дифракционной длины (m< 1). Схема для наблюдения дифракции Фраунгофера приводится на рис. Точечный источник света помещают в фокусе собирающей линзыL₁, получая плоскую волну, падающую на препятствиеЭ₁;за препятствием помещают вторую собирательную линзуL₂и дифракционную картину исследуют в ее фокальной плоскости на экране Э₂.

3.2.3. ДИФРАКЦИЯ НА ПРЯМОУГОЛЬНОЙ ЩЕЛИ. Пусть плоская волна падает на прямоугольную щель шириной b. По принципу Гюйгенса пучок параллельных лучей, проходя через щель, дифрагирует под всевозможными углами в пределах от 0 до π/2.

Все лучи, падающие по нормали к плоскости щели (φ = 0), находятся в одной фазе (рис. а), поэтому в центре экрана возникает светлое пятно. Это соответствует главному или нулевому максимуму интенсивности. Он самый яркий.

Вторичные волны за плоскостью щели можно сгруппировать в параллельные пучки, из всей совокупности которых на рис.б представ-лены два. Для лучей, идущих под углом  от крайних элементов щели, разность хода Δ_д, равна:

Δ_д = b sin .

Разделим ширину щели b на зоны Френеля: плоские полоски, вытянутые вдоль щели. В разности хода Δ_д уложится N зон Френеля:

N = Δ_д / ( / 2) = b sin  / ( / 2).

Если в направлении φ открыто

• четное число зон N=2m,, то амплитуда результирующей волны E_m(φ) = 0 и в этих направлениях наблюдаются минимумы интерференции:

Δ_дmin = b sin  = m.

• нечетное число зон N = (2m + 1), то наблюдаются максимумы интерфе-ренции:

Δ_дmax = b sin  = (2m + 1)  /2.

причем, m = 1, 2, 3 и т. д. – порядок дифракции.

Интенсивности дифракционных максимумов по отношению к нулевому составляют следующий ряд чисел:

I₀ : I₁ : I₂ : I₃ = 1 : 0.045 : 0.016 : 0.008.

Распределение интенсивности при дифракции на щели

Как видно, основная энергия световой волны при дифракции на щели сосредоточена в пределах нулевого максимума, т.е. в пределах угла sin = ± λ/b и интенсивность достаточно сильно (как 1/m²) убывает с ростом порядка максимума. Точное выражение для распределения интенсивности света на экране:

I() = I₀ (sinA/A)² ,

где I₀ – интенсивность центрального максимума, параметр A = b(sin ) /.