4.3. Проектирование цифрового регулятора

Дифференциальное уравнение, описывающее динамику движения магнитной головки записи-считывания жесткого диска, можно на основе закона Ньютона записать в следующем виде:

где J– момент инерции головки;

С – коэффициент вязкого трения в подшипниках;

К – коэффициент жесткости пружины;

К_i – моментный коэффициент двигателя;

 – угловое положение головки;

i– ток якоря двигателя;

Для привода жесткого диска необходимо задать следующие числовые данные: J=0.01кгм², С=0.004 Нм/(рад/c), К=10 Нм/рад,K_i=0.05 Нм/А.

1. Необходимо получить передаточную функцию привода жесткого диска.

2. Перейти от непрерывной модели объекта управления к дискретной с периодом дискретизации 0.005 с, используя экстраполятор 0-порядка Wd=c2d(Wn,ts,’zoh’).

3. Построить переходные и частотные характеристики непрерывной и дискретной модели.

4. Провести анализ показателей качества управления.

5. Найти значение полюсов дискретной системы (pole(Wd),rlocus(Wd)).

6. Вести компенсатор с передаточной функцией Wr(z)=(z+a)/(z+b), где а=-0.85;b=0 (Wr=zpk(0.85,0,1,Ts)).

7. Вызвать функцию rltoolдля настройки коэффициента регулятора замкнутой системы с целью улучшения показателей качества регулирования.

8. Рассчитать запасы устойчивости системы.

9. Сделать выводы о проделанной работе.

4.4. Содержание отчета

Отчет оформляется в соответствии с требованиями, предъявляемыми к оформлению лабораторных работ в вузе, и должен содержать:

1. Титульный лист.

2. Формулировку цели работы.

3. Постановка задачи в соответствии с заданием.

4. Передаточную функцию исследуемой САР.

5. Результаты работы.

6. Выводы.

4.5. Контрольные вопросы

1. Как зависят показатели регулирования дискретной САУ от расположения корней характеристического уравнения?

2. В чем заключается задача синтеза САУ?

3. Какие типы САУ позволяет моделировать функция rltool?

4. Как записать дискретную передаточную функцию дискретной САУ по дифференциальному уравнению?

5. Какой класс систем позволяет моделировать библиотека controlsystemtoolbox?

6. Какой подкласс более предпочтителен для моделирования систем?

5. РЕЛЕЙНЫЙ РЕГУЛЯТОР УРОВНЯ ЖИДКОСТИ В РЕЗЕРВУАРЕ

1. Цель лабораторной работы

Исследовать показатели качества регулирования уровня жидкости в резервуаре цилиндрической формы, получить навыки организации нелинейных САУ в ППП Simulink.

5.2. Краткие сведения из теории

Рассмотрим динамическую модель объекта регулирования – резервуар. Схема резервуара представлена на рисунке 5,1.

Рис. 5.1. Схема гидравлического объекта–резервуара.

Баланс жидкости в резервуаре определяется входным q₁и выходным потокомq₂. Количество жидкостиQ(t)в каждый момент времениt>0 определяется его начальным значениемQ₀=Q(0)и накоплением за времяt>0 как:

Q(T)=Q₀+, (1)

где q=q₁–q₂.

Преобразование (5.1) в модели реализуется типовым звеном интегратором (см. рисунок 5.1). Выход интегратора соединен с коэффициентом передачи Gain, который вычисляет уровень жидкостиh(t)для резервуара цилиндрической формы определяется согласно формуле:h(t)=Q(t). Это означает, что для расчетаh(t)величинуQ(t)надо умножить на постоянный коэффициентk_h=. Аналитическую модель процесса заполнения или опустошения бака обычно стремятся записать в виде дифференциального уравнения:с начальным условиемh(0)=h₀. Для того чтобы учесть высоту резервуара необходимо использовать блокSaturation. Данный элемент представляет статическую характеристику типа блок усиления с зоной насыщения.

Если резервуар имеет форму воронки или шара, то в этом случае зависимость уровня h(t)от объема водыQ(t)будет уже не прямо пропорциональной, а нелинейнойh=N_h(Q). Пусть теперь жидкость свободно вытекает через отверстие с проходным сечениемв днище бака. В этом случае скорость истечения жидкостизависит от ее уровняh, а расходq₂=пропорционален сечениюотверстия. Зависимость скорости истечения идеальной жидкостииз отверстия от высоты ее открытой поверхностиhнад отверстием описывает формула Торричелли .

Элементы Gain1 иFcn(см. рис. 5.2) реализуют внутреннюю обратную связь в системе: расходq₂(t)теперь не является независимой переменной, а определяется уровнем жидкостиh(t)над отверстием.

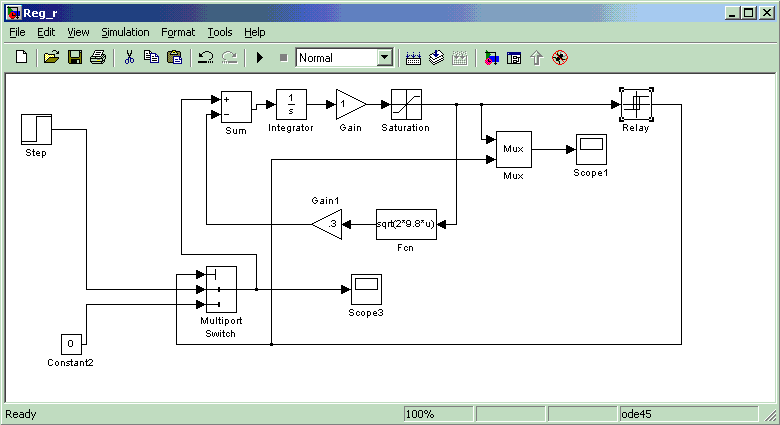
Рис. 5.2. Структурная схема моделирования релейной системы