Нормальное распределение. Свойства нормального распределения
1. Дана случайная
величина
 . Вычислить вероятность
. Вычислить вероятность
 .
.
2. Найти плотность
распределения случайной величины Y
= X2 , если случайная
величина X имеет нормальное
распределение с параметрами a
= 0, σ2
= 1, т.е.
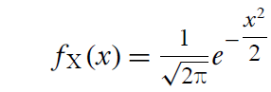
3. Случайная
величина X распределена
нормально с математическим ожиданием
а = 10. Вероятность попадания X
в интервал (10, 20) равна 0.3. Найти вероятность
попадания X в интервал
(0, 10).
Предельные теоремы. Неравенство Чебышева. Закон больших чисел
1. В 400 испытаниях
Бернулли вероятность успеха в каждом
испытании равна 0,8. С помощью неравенства
Чебышева оценить вероятность того, что
разница между числом успехов в этих
испытаниях и средним числом успехов
будет меньше 20.
2. Случайная
величина распределена по стандартному
нормальному закону. Оценить снизу
вероятности событий
А = (-2 < X < 2), B
= (-1 < X < 1). Найти значения
вероятности этих событий.
3. В партии
лампочек накаливания содержится 1000
штук изделий. С вероятностью 0.01 лампочка
имеет дефект нити накаливания и независимо
от этого события с вероятностью 0.03
дефект цоколя. Найти границы, в которых
будет, практически наверняка, содержатся
бракованные лампочки. Считать, что
практическая достоверность равна 0.95 .
4. Монету подбрасывают
1000 раз. С какой вероятностью можно
гарантировать выполнение неравенства:

Преподаватель
кафедры Информатики и математики
В. Крупчатников
23..01.2016