
Lektsia_19
.pdfЛекція 19. Наближенні обчислення за допомогою степеневих рядів.
Наближенні обчислення значень функцій.
|
Нехай треба обчислити значення функції |
при |
|||
|
. Якщо функцію |
можна розкласти в |
|
||
степеневий ряд в інтервалі |
і |
|
, то |
||
точне значення |
дорівнює сумі цього ряду при |
||||
|
, а наближене частинній сумі |
. |
|
||
|
Похибку | |
|
| можна знайти, оцінюючи |
||
залишок ряду |
. Для рядів лейбніцевого типу |
||||
| |
| | |
|
| |
| |
| |
Для знакозмінних і знакододатних рядів величину
, як правило, оцінюють так:
| |
| |
| |
| |
| |
| |
| |
| |
|
|
|
|
|
|
де |
ak |
– певний знакододатний збіжний ряд, |
|||
|
k 1 |
|
|
|
|
сума якого |
легко обчислюється (наприклад, |
||||
геометрична прогресія), і для якого |
|
||||
| |
| |
| |
| |
| |
| |

Значення синуса та косинуса обчислюються за наближеними формулами ( виражене в радіанах)
Похибка оцінюється за допомогою нерівності:
| |
| |
Похибка оцінюється за допомогою нерівності
| |
| |
Для обчислення логарифмів використовують формулу:
Підставляючи замість значення |
матимемо |
ряд |
|
Тоді

( )
( |
|
|
|
|
|
) |
|
|
|
Похибка цієї формули оцінюється нерівністю
| |
| |
| |
|
|
|
|
| |
|
|
|
|
|
|||||
| | |
|
|
| |
| |
||||
|
|
|
|
|
|
|
|
|
Приклад 1. |
|
|
Обчислити з точністю до |
: |
|
а) значення |
; б) число . |
|
а) Використовуючи формулу
Дістали ряд лейбніцевого типу. Оскільки
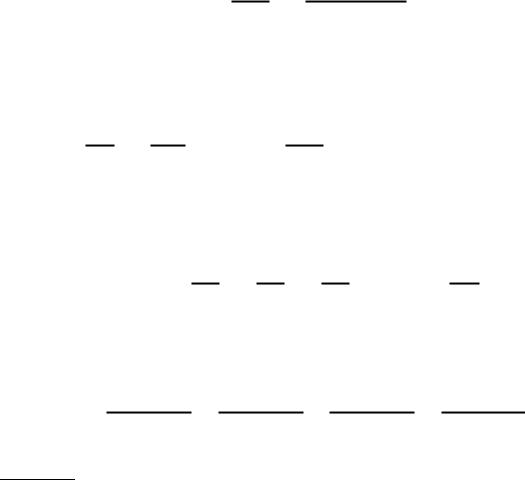
то з точністю до |
маємо |
б) підставивши в ряд
, знайдемо знакододатний ряд
Оцінимо -ий залишок цього ряду:
( |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
) |
|
( |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
) |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Знайдемо таке найменше натуральне число , щоб
виконувалась нерівність |
|
|
. |
|
|
||||
Ця нерівність виконується при |
, тому з точністю |
|||
до |
маємо |
|
||

Наближене обчислення визначених інтегралів.
Нехай потрібно знайти інтеграл |
∫ |
, |
|
який або не виражається через елементарні функції, |
|
||
або складний і незручний для обчислень. |
|
|
|
Якщо функцію |
можна розкласти в степеневий |
||
ряд, що рівномірно збігається на деякому відрізку, то для обчислення заданого інтеграла можна скористатись властивістю про почленне інтегрування цього ряду.
Похибку обчислень визначають так само, як і при обчислені значень функцій.
Приклад2.
Обчислити інтеграл ∫ |
|
з точністю до |
. |
|
Використовуючи формулу
Запишемо підінтегральну функцію у вигляді
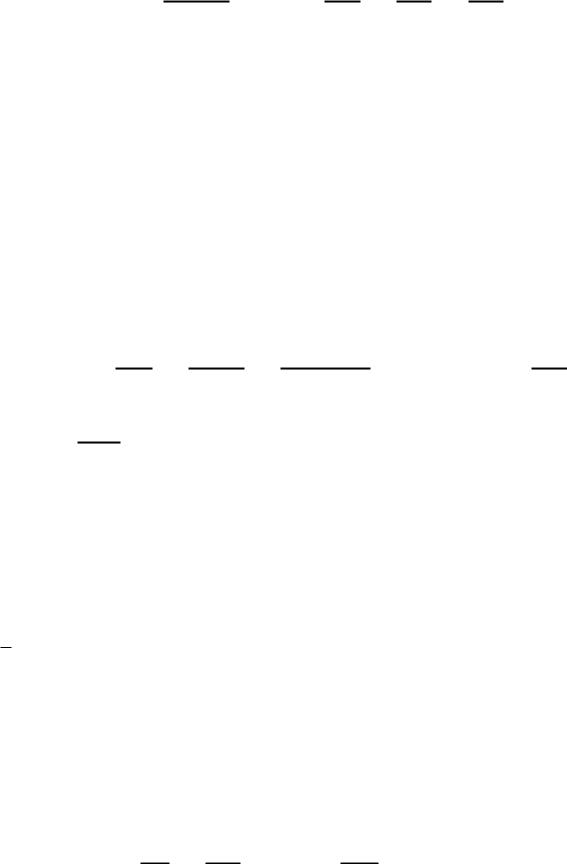
тоді
∫ |
|
∫ ( |
|
|
|
|
|
) |
|
|
|
|
( |
|
|
|
|
|
) | |
|
|
|
так як і всі члени, які менші від заданої
точності, відкидаємо.
Приклад 3.Обчислити з точністю до |
інтеграл |
1
3
e x2 dx
0
Скориставшись рядом
маємо
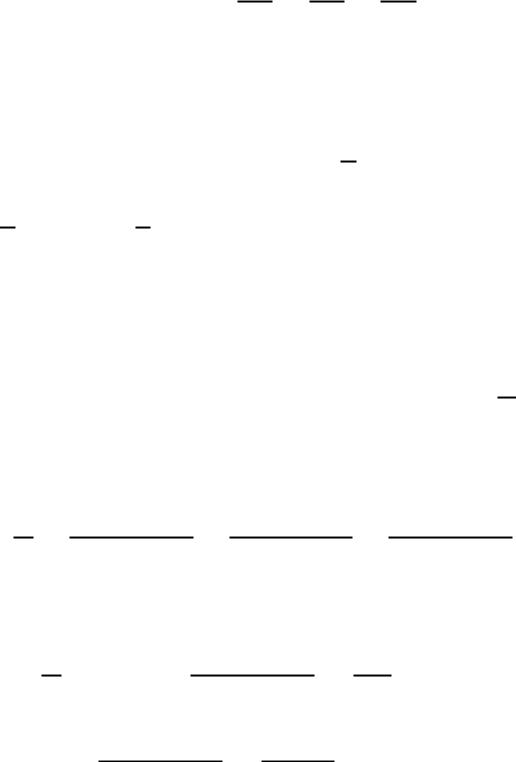
Цей ряд рівномірно збіжний на всій числовій осі, тому його можна почленно інтегрувати на будь-якому
відрізку, зокрема на відрізку * +:
∫ |
∫ ( |
|
|
|
|
|
) |
|
|
|
( |
|
|
|
|
|
) | |
|
|
|
Дістали ряд лейбніцевого типу. Оскільки
то з точністю до |
маємо |

∫
Первісна для функції не є елементарною функцією. Проте її легко знайти у вигляді степеневого ряду, проінтегрувавши ряд для
функції в межах від до .
∫ |
∫ ( |
|
|
|
|
|
) |
|
|
|
Приклад 3.
Обчислимо з точністю |
інтеграл |
∫
Розкладемо функцію |
у ряд Маклорена: |
∫ √ ∫

∫ (
)
∑ |
|
|
|
| | |
|
|
Розділимо цей ряд на і проінтегруємо на відрізку
*+, що належить області збіжності ряду, отримаємо
∫(
)
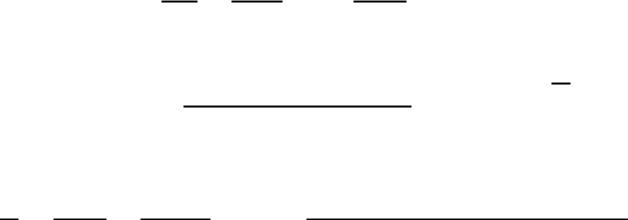
(
) |
Оцінимо |
-ий залишок ряду |
|
|||||||||||||
| |
|
( |
|
)| |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|||||||||
( |
|
|
|
|
|
|
) |
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Нерівність | |
( |
|
)| |
виконується при |
, |
||||||||||
|
|||||||||||||||
тому беремо 2 члени ряду для обчислення інтеграла з точністю :
|
|
|
|
|
|
|
|
. |
∫ |
|
|
|
|
|
|||
|
|
|
||||||
