
FKS
.pdf11
kx , k y , kz визначаються відповідно числами 1 , 2 , 3 , тобто складові хвильового вектора
змінюються дискретно або мають дискретний спектр. Відповідно і сам вектор k має дискретний спектр.
10. Хвильові функції вільних електронів у кристалі.
Хвильову функцію вільних електронів в кристалі треба знаходити з рівняння Шредінгера для стаціонарного стану, тобто коли потенціальна енергія
U (r ) 0 .
Рівняння Шредінгера:
(2-1)
де, ∆ - оператор Лапласса; (r) - хвильова функція вільного електрону;ħ – стала Планка; m –
маса електрона; Е – енергія (кінетична).
В одновимірному випадку рівняння має вигляд:
(2-2)
Позначимо вираз:
(2-3)
Параметр к пов’язаний з енергією електрона і від нього залежить хвильова функція. Він відіграє дуже важливу роль в квантовій теорії твердого тіла(2.
d-4)
Знайдемо розв’язок рівняння (2-4). Розв’язок цього рівняння має вигляд:
-5)
де, r1, r2 – корні характерного рівняння:
d-6) -7)
-8)
де, і = √-1
Тоді загальний розв’язок рівняння буде мати вид:
r-9)
Індекс k в рівнянні (2-9) ми пишемо тому, що хвильова функція залежить від k, як від параметру. Окремі розв’язки:
(2-10)
(2-11)
В результаті цих розрахунків можна зробити висновок:
вільний електрон в кристалі може перебувати в трьох станах з хвильовими функціями (2-9), (2- 10), (2-11).
Графічно хвильова функція може бути представлена, як плоска хвиля, що поширюється у напрямку осі ох.
12
11.Кількість квантових станів в зоні Бріллюена (густина станів у зоні Бріллюена).
Із визначення витікає, що всі зони Бріллюена мають однакове число квантових станів. Визначимо в яких межах змінюються складові вектору k. В першій зоні Бриллюена:
kx [-π/a1; π/a1], ky
За циклічними умовами Борна-Кармана:
kx |
2 1 , |
|
|
|
|
2 1 |
|
|
|
|||||||
|
|
|
|
|||||||||||||
|
a1 n1 |
|
|
a1 |
|
|
|
a1n1 |
|
|
|
|
a1 |
|||
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|||||
|
|
|
|
|
2 |
|
|
|
|
|
||||||
(7.4) |
|
|
a2 |
|
a2n2 |
|
a2 |
|||||||||
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
2 3 |
|
|
|
|
|
|
|
|
|
|
|
a3 |
|
|
a3n3 |
|
|
|
a3 |
||||||
|
|
|
|
|
|
|
|
|
|
|
||||||
[-π/a2; π/a2], kz [-π/a3; π/a3] (7.3)
k |
|
|
2 |
|
1 |
k |
|
|
2 |
|
2 |
k |
|
|
2 |
|
3 |
x |
a1 |
|
n1 |
y |
a2 |
|
n2 |
z |
a3 |
n3 |
|||||||
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
Об’єм основної області кристалу:
V0=(a1n1)(a2n2)(a3n3) (7.5)
|
|
|
|
|
a1n1 |
|
1 |
|
|
|
a1n1 |
|
|
n1 |
1 |
|
|
n1 |
(7.6) |
||||||||||||||
|
a |
2 |
a |
2 |
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
2 |
|
|
|
||||||||||||||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a2 n2 |
|
|
2 |
|
|
|
|
a2 n2 |
|
|
|
|
n2 |
|
|
2 |
|
n2 |
|
(7.7) |
||||||||
a |
|
|
|
a |
|
|
|
|
|
|
|
||||||||||||||||||||||
|
2 |
|
|
|
|
2 |
|
|
|
|
|
|
2 |
2 |
|
|
|
2 |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a3 n3 |
|
3 |
|
|
|
a3 n3 |
|
|
n3 |
|
3 |
|
n3 |
|
(7.8) |
|||||||||||||
|
a |
|
|
|
|
a |
|
|
|
|
|||||||||||||||||||||||
|
|
3 |
|
|
|
|
2 |
|
|
|
|
|
|
2 |
2 |
|
|
|
2 |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Зцих формул видно, що 1 може приймати n1 значень
2 може приймати n2 значень
3 може приймати n3 значень
Оскільки 1 , 2 , 3 змінюються незалежно, то максимальне число різних складових
хвильового вектора k в межах зони Бріллюена (відповідно і число вектора k в цій зоні) буде дорівнювати n1n2n3 .З формули (7.5) знайдемо:
n1n2n3 = V0/a1a2a3 (7.9)
Тоді (7.9) визначає кількість елементарних комірок в об’ємі V0. Оскільки примітивній комірці належить один атом, то вираз (7.9) визначає атомів кількість в цьому кристалі. Оскільки в типових металах електронний газ складається з електронів, кількість яких дорівнює кількості атомів N, то кількість можливих станів в зоні Бріллюена дорівнює числу атомів в даному кристалі. Якщо врахувати, що згідно принцупу Паулі, в одному стані можуть знаходитись 2 електрона, то їх кількість, що визначається одної зоною Бріллюена становить 2N, тобто електронним станом на один атом
13
12. Квазіімпульс електрона у кристалі.
Для аналіза фізичних властивостей, які визначаються рухом електронів (електропровідність, теплопровідність, надпровідність, ефект Хола) треба знати за якими законами рухаються електрони, під дією зовнішніх сил. Якщо на електрон не діють зовнішні сили, то він знаходиться в стані, що визначається хвильовою функцією:
(5-4) (5-8)
Використовуючи методи квантової механіки можна показати, що середня швидкість |
|
|
|
електрона < > в стані з хвильовою функцією дорівнює похідній від енергії по вектору : |
|
|
(8-1) |
або в одновимірному випадку |
|
|
(8-2) |
Ця залежність не є абсолютно новою, оскільки для вільного електрона: |
|
|
(8-3) |
|
(2-14) |
E |
|
|
(8-4) |
|
(8-5) |
Формула (8-5) співпадає з формулою (8-2).
кристалічної гратки такий звязок не існує, крім того стан електрона в періодичному полі кристалічної гратки – це стан в якому імпульс і відповідно швидкість не мають визначеного значення, тому у формулі (8-1) і (8-2) стоять середні значення швидкості.
Формула (2-14) виконується для вільного електрона. Для електрона в періодичномуvполі
З’ясуємо фізичний зміст вектора k в формулі (5-4).
Нехай на електрон в кристалі діє зовнішня сила . Розглянемо одновимірний випадок.
Якщо електрон під дією цієї сили переміститься на відстань |
, то робота цієї сили буде |
|||
дорівнювати і ця робота буде дорівнювати зміній енергії електрона |
: |
k(8-6) |
||
Розділим це рівняння на |
: |
|
|
|
|
Edt |
|||
(8-7) |
|
(8-8) |
|
k |
Підставимо формулу (8-2) у формулу (8-8): |
|
|||
|
(8-v9) (8-10) |
|
||
vk

|
2 |
|
|
|
|
|
|
|
|
|
|
|
14 |
Таким |
чином величина |
(характеристика електрона в періодичному полі |
||||
кристалічної гратки) має значення імпульса електрона, оскільки її приріст дорівнює імпульсу |
||||||
сили за час |
: |
|
|
|
|
|
|
|
|
|
|
(8-11) |
|
|
|
dk(11 |
||||
Тому, для електрона в кристалі велечина |
називається квазіімпульсом. |
|
|
|||
Закон збереження квазіімпульса електрона в кристалі формується так: |
(8-12) |
|||||
13. Ефективна маса електрона у кристалі.
Введені поняття ефективної маси електрона дозволяє зробити опис деяких фізичних властивостей кристалічних речовин.
Припустимо, що ми вже знаємо ефективну масу електрона. Тоді другий закон Ньютона буде мати вигляд:
m |
d |
|
|
F |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-1) |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
m |
|
|
|
F |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-2) |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
d |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
d |
|
|
|
d |
1 |
|
|
|
dE |
1 |
|
|
|
2 E |
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|||||||||||||
|
dt |
|
|
|
|
|
|
dt |
|
|
|
dk |
|
|
|
|
|
dt |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
dk |
|
1 |
F |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(8-1) |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
d |
|
|
1 |
|
|
|
d E |
|
F |
|
|
|
|
|
|
|
|
|
|
-3) |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
dt |
|
|
|
|
|
2 |
|
dk 2 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Підставимо (11-3) в (11-2) |
|
|
|
|
|
|||||||||||||||||||||||||||||||
m |
|
|
|
|
F |
|
|
|
|
|
|
|
|
|
|
F |
|
|
|
|
|
2 |
|
|
(11-4) |
|||||||||||
|
|
d |
|
|
|
|
|
1 d 2 E |
|
|
|
|
d 2 E |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F |
|
t |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
dk 2 |
|
dk 2 |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
Поняття про ефективну масу електрона дозволяє пояснити наявність в напівпровідниках електронної та діркової провідності.
14. p–провідність у напівпровідниках.
Чистий напівпровідник при 00 К – це кристал з повністю заповненою першою зоною Бріллюена та пустою другою зоною Бріллюена
Носії Р типу існують в першій зоні Бріллюена. Квантові стани можуть переходити в вільні місця
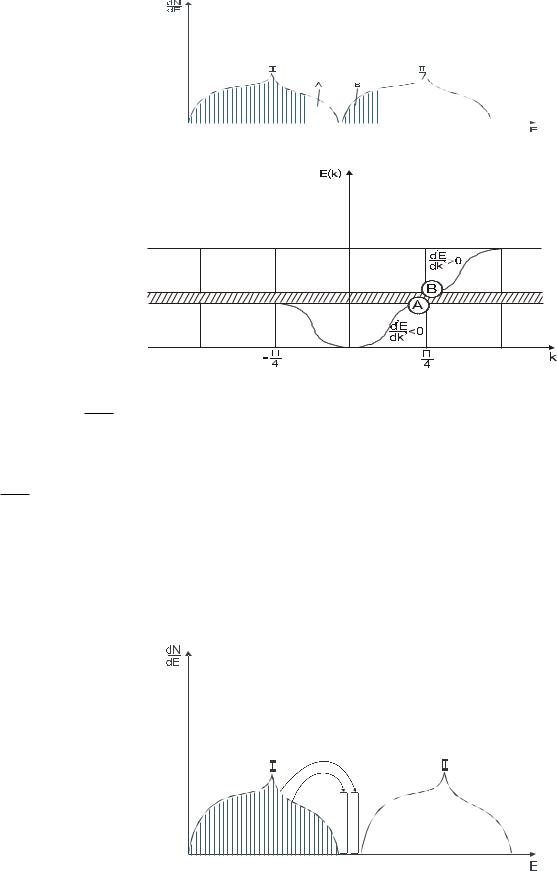
15
Таким чином в чистому напівпровіднику при підвищені температури виникають носії зарядів двох типів.
m |
|
2 |
0 |
(11-5) |
|
|
|||
|
|
|||
|
d 2 E |
|
||
dk 2
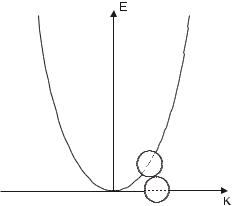
В вільній ділянці першої зони (А) електрони будуть мати від’ємну масу (11-5). Тому, що ця ділянка відповідає кривій Е від k, де перша похідна зменшується і відповідно друга похідна
d 2 E 0 . dk 2
Це означає, що електрони в цій ділянці ведуть себе як частинки з від’ємною масою і від’ємним зарядом, тобто як частинки з позитивним зарядом і позитивною масою, з точки зору переносу заряду. Це і є – Р-провідність.
Домішкова провідність пояснюється таким чином. Якщо напівпровідник легований якимось елементом, то в забороненій зоні виникають додаткові енергетичні рівні.
Якщо ці рівні вільні, то на них можуть переходити електрони з першої зони Бріллюена і в цьому випадку виникає домішкова провідність (Р-провідність). Ця домішка називається акцепторна домішка. При цьому переході виникають вільні стани.
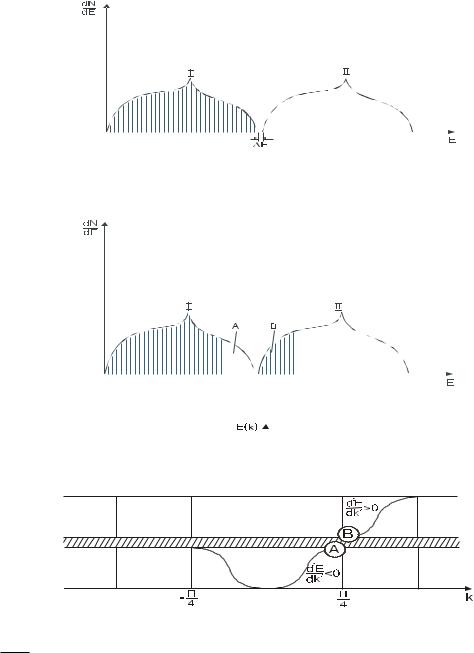
16
15. n–провідність у напівпровідниках.
Чистий напівпровідник при 00 К – це кристал з повністю заповненою першою зоною Бріллюена та пустою другою зоною Бріллюена
Носії Р типу існують в першій зоні Бріллюена. Квантові стани можуть переходити в вільні місця
Таким чином в чистому напівпровіднику при підвищені температури виникають носії зарядів двох типів.
m |
|
2 |
0 |
(11-5) |
|
|
|||
|
|
|||
|
d 2 E |
|
||
dk 2
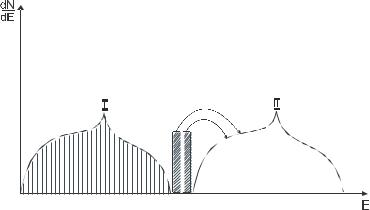
|
|
17 |
|
На ділянці В другої зони Бріллюена, друга похідна |
d 2 E |
0 оскільки ця ділянка |
|
dk 2 |
|||
|
|
відповідає області В графіка Е(k). Тому, електрони тут мають позитивну та ефективну масу, тобто ведуть себе як нормаль електрона. Тут здійснюється n-провідність.
Домішкова провідність пояснюється таким чином. Якщо напівпровідник легований якимось елементом, то в забороненій зоні виникають додаткові енергетичні рівні.
Якщо домішкові рівні зайняті електронами, то при підвищені температури електрони з них переходять у другу зону і в цьому випадку реалізується n-провідність. Легуючий елемент називається донорною домішкою.
Дискретність спектру хвильового вектора електрона у кристалі як наслідок виконання циклічних умов Борна-Кармана.
Властивість періодичності функції (r) можна записати:
k
(3-5) (3-6) (3-7) (3-8) (3-9) (3-10)
(3-11)
Умови (3-10), (3-11) виконуються при значеннях:
k |
x |
n a |
2 |
1 |
1 |
0, 1, 2... |
|
|
1 1 |
|
|
|
|
||
k y n2 a2 |
2 2 |
2 |
0, 1, 2... |
(3-12) |
|||
k |
z |
n a |
3 |
2 |
3 |
|
3 0, 1, 2... |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
18 |
З (3-12) витікає: |
|
|
|
|
|
|
|
|
|
|
|
kx |
|
2 |
|
|
1 |
|
|
||||
a1 |
|
n1 |
|
||||||||
|
|
|
|
|
|
|
|||||
k y |
|
2 |
|
|
|
2 |
|
|
|
||
a2 |
|
n2 |
(3-13) |
||||||||
|
|
|
|
|
|
||||||
kz |
|
2 |
|
|
|
3 |
|
|
|
||
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a3 |
|
|
|
n3 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
Формули (3-13) визначають можливі значення |
складових хвильового вектора k |
||||||||||
електрона в кристалі. Оскільки а1, а2, а3 та n1, n2, n3 фіксовані для даного кристалу числа, то kx , k y , kz визначаються відповідно числами 1 , 2 , 3 , тобто складові хвильового вектора
змінюються дискретно або мають дискретний спектр. Відповідно і сам вектор k має дискретний спектр.
Оскільки n1, n2, n3 великі цілі |
числа, а сусідні значення 1 , 2 , 3 |
|
відрізняються на |
||
одиницю, то сусідні значення kx , k y , kz |
дуже близькі і відрізняються на |
|
1 |
|
. Тобто спектр |
|
|
|
|||
|
|
|
|||
|
10000 |
|
|||
можливих значень величини к в принципі дискретний, але практично є неперервний і має назву “квазінеперервний”. Це можна сказати і про спектр можливих значень енергії електрона в кристалі. Якщо розглядати під збільшенням ділянки графіка Е~ f (k) та осі k, то можна побачити, що вони складаються з окремих близько розташованих одна від одної точок.
Рис.1.1
