Практикум 2

Розділ 7. ДИФЕРЕНЦІАЛЬНЕ ЧИСЛЕННЯ ФУНКЦІЙ ОДНІЄЇ ЗМІННОЇ

61

7.4. Формули для похідних вищих порядків

Похідні вищих порядків

f (x) (f (x)) ,

f

(n)

(f

(n 1)

(x)

(x)) , n

Позначення

(4)

(n)

y , y

, y

, ..., y

, ...;

Диференціали вищих порядків

d

2

f(x0) d(df(x0)),

dn f (x

0

) d(dn 1f(x

0

))

Інваріантність 1-го диференціала

df(u(x)) f (u)du, u u(x)

Формула обчислення диференціала

d

n

f (x0 ) f

(n)

(x0 )dx

n

,

де x — незалежний аргумент

Лейбніцова формула

u(x)v(x) (n)

n

Cnku(n k)(x)v(k)(x)

k 0

u(0) u, v(0)

v

Похідна параметрично заданої

x(t),

x

функції

y

(n)

y

(n 1)

(t)

x(t),

(x) :

n 1

x

(n)

x

t

y(x) :

, t ( ; )

y(t), t ( ; )

y

n (t)

x (t)

y

x

t

Похідні вищих порядків деяких функцій.

m !

m n

(n)

n

1

( 1) n !

x

,

n m,

(x

m (n)



n 1



)

(m n)!

0,

n m

x a

(x a)

m

(ax )(n)

ax (ln a)n

(ex )(n)

ex

(log x)(n)

( 1)n 1(n 1)!

(ln x)(n)

( 1)n 1(n 1)!

a

xn ln a

xn

(n)

n

n

(n)

n

n

x

cos

x

(sin x)

sin

(cos x)

2

2

Дотична і нормаль до кривої.

y

Дотичною до кривої в точці M0

y0 y

M

називають пряму M0T, що є

T

граничним положенням січної M0M,

f(x0 )

коли точка M прямує по кривій до

точки M0.

df(x0 )

y0

M0

x

O

x0

x0 x

x

Нормаллю до кривої називають

y

дотична

пряму, яка перпендикулярна до

y0

дотичної і проходить через точку

y f (x)

дотику.

нормаль

O

x0

x

Геометричний зміст похідної і диференціала в точці

Похідна функції f(x) у точці x0

f (x0 ) tg ,

дорівнює кутовому коефіцієнту

де — кут нахилу дотичної до осі

дотичної, проведеної до графіка

Ox.

функції y f(x) у точці

Диференціал функції дорівнює

M0(x0; f (x0 )), тобто

приросту ординати дотичної.

Рівняння дотичної

f (x0 )

y f (x0 ) f (x0 )(x x0 )

f (x

0

)

x

x

0

Рівняння нормалі

f (x0) 0

y f(x0)

1

(x x0 )

f (x0 )

f (x

0

) 0

x

x

0

Розділ 7. ДИФЕРЕНЦІАЛЬНЕ ЧИСЛЕННЯ ФУНКЦІЙ ОДНІЄЇ ЗМІННОЇ

63

Теорема Роля. Якщо функція f (x) :

y

C

3) на кінцях відрізку [a;b] набуває

m

рівних значень f (a) f (b), то в

O

a

b x

інтервалі (a;b) існує принаймні одна

точка , така, що

На графіку функції існує точка M,

f ( ) 0, (a;b).

дотична в якій паралельна осі Ox.

Теорема Лаґранжа.

y

B

Якщо функція f (x) :

C

1) неперервна на відрізку [a;b],

2) диференційовна в інтервалі (a;b),

A

то в інтервалі (a;b) існує принаймні

одна точка така, що

O

a

b x

f (b) f (a) f

( )(b a), (a;b).

На графіку функції існує точка C,

дотична в якій паралельна січній AB.

Теорема Коші.

Правило Бернуллі — Лопіталя.

Якщо функції f (x), g(x):

Якщо функції f (x), g(x):

1) означені і диференційовні у

1) неперервні на відрізку [a;b],

проколеному околі точки x0,

2) диференційовні в інтервалі (a;b),

2) g (x) 0 в цьому околі,

3) lim

f(x) lim g(x) 0

( ),

3) похідна g (x) 0 в інтервалі (a;b),

то в інтервалі (a;b) існує принаймні

x x0

x x0

f (x)

одна точка така, що

4) існує

lim

A,

g (x)

f(b) f(a)

f ( )

x x0

то існує

g(b) g(a) g ( ) , (a;b).

f(x)

0

lim

або

A.

x x

0

g(x)

0

Многочлен Тейлора n -го порядку

n

f (k)(x0 )

k

функції f (x) за степенями (x x0 )

Pn(x)

(x

x0 )

k !

k 0

Формула Тейлора n -го порядку

n

(k)

(x0 )

для функції f (x) в околі точки x0

f (x)

f

(x x0 )k

Rn(x)

k 0

k !

Формула Тейлора — Маклорена

n

f

(k)

для функції f (x) в околі точки x0 0

f (x)

(0)

xk

Rn(x)

k 0

k !



Залишковий член формули Тейлора

(x)

Rn(x) f(x) Pn

Залишковий член у формі Пеано

n

x0

Rn(x) o((x x0 ) ), x

Залишковий член у формі

f

(n 1)

Лаґранжа

Rn

(x)

( )

(x x0 )n 1, (x0; x)

(n 1)!

f (x) f (x

0 )

f (x

0 )

(x x0 ) ...

f (n)(x0 )

(x x

n

o((x x

n

0 )

0 ) ),

1 !

n !

 ex 1 x x2

... xn

e

xn 1

,

(0; x)

2 !

n !

(n 1)!

 ln(1 x) x x

2

... ( 1)n 1 x

n

( 1)n

xn 1

2

n

(1 )n 1 n 1

 sin x x x3

... ( 1)n 1

x2n 1

( 1)n cos

x2n 1

3!

(2n 1)!

(2n 1)!

 cos x 1 x2

x4 ... ( 1)n

x2n

( 1)n 1 cos

x2n 2

2!

4 !

(2n)!

(2n 2)!

k співмножників

n 1 співмножник

n

( 1)

... ( k

1)

( 1) ... ( n)

(1 x) 1

xk

xn 1

k 1

k !

(1 )n 1(n 1)!

Розділ 7. ДИФЕРЕНЦІАЛЬНЕ ЧИСЛЕННЯ ФУНКЦІЙ ОДНІЄЇ ЗМІННОЇ

65

7.8. Асимптоти. Екстремуми. Точки перегину

Асимптота. Асимптотою кривої з

y

y f(x)

нескінченною гілкою називають таку

пряму, що віддаль d точки M кривої до

M

цієї прямої прямує до нуля, коли точка

d

M віддаляється вздовж нескінченної

гілки від початку координат.

O

x

Вертикальна асимптота. Пряма

y

y

x x0 є вертикальною асимптотою

графіка функції y f(x), якщо

lim f(x) .

x

x x0

x0

x

0

x

Похила асимптота y = kx + b.

lim

f(x) k,

Графік функції y f(x) має похилу

x

x

асимптоту y kx b, тоді й лише

lim (f(x) kx) b.

тоді, коли існують скінченні границі

x

Екстремум функції в точці. Якщо існує такий -окіл точки x0,

що для всіх

x U (x0 ) \ {x0 } виконано нерівність:

 f(x0 ) f(x) f(x0 ) 0,

y

max

max

max

то точку x0 називають точкою

строгого локального максимуму

функції f (x), а значення f(x0 ) —

локальним максимумом функції;

 f(x0 ) f(x) f(x0 ) 0,

min

min

min

то точку x0 називають точкою

O

x

строгого локального мінімуму функції

Точки максимуму і мінімуму

f (x), а значення f(x0 ) — локальним

називають точками екстремуму

мінімумом функції.

функції, а максимуми та мінімуми

функції — екстремумами функції.

Точка перегину. Точку x0

y

називають точкою перегину функції

f (x), якщо під час переходу через неї

функція змінює напрям опуклості на

O

x

протилежний.

Критична точка 1-го порядку.

1)

f (x0 ) 0;

Нехай функція f (x) означена в околі

2) f (x0 ) ;

точки x0. Точку x0 називають

3)

f (x0 ).

критичною точкою 1-го порядку, якщо

виконано одну з умов:

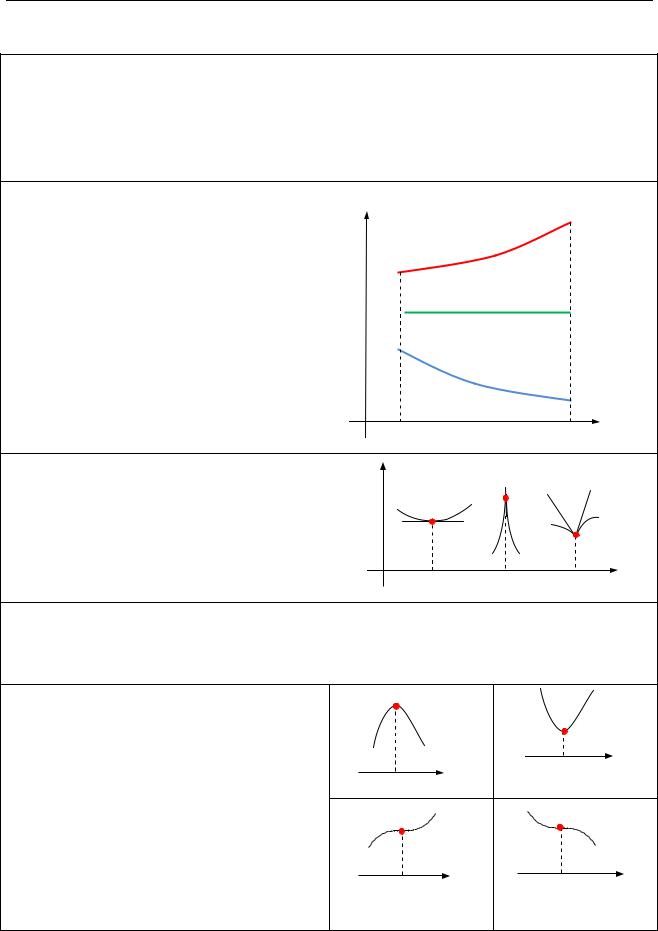
Достатня умова монотонності