
Практикум 2
.pdf
|
Розділ 4. МНОЖИНИ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
11 |
|
||||
|
4.6. Числові множини |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Запис числа у десятковій системі |
|
|
|
|
|
|
n ... 1 0 |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
n |
10n |
... 10 |
|
, |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
0 |
|
|
|||
|
|
|
i |
{0, 1, 2, 3, 4, 5, 6, 7, 8, 9} |
|
|
||||||||||||||||||
|
Запис числа у двійковій системі |
|
|
|
|
|
|
n ... 1 0 |
|
|
|
|
|
|||||||||||
|
|
|
n 2n |
... 1 2 0, |
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
i {0, 1} |
|
|
|
|
|||||||||||
|
Десяткові дроби (a , i, i {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}) |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
скінченний |
|
|
|
|
|
|
|
a, 1 2... n |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
нескінченний періодичний |
|
a, 1 2... n ( 1 2... k ) |
|
|
|||||||||||||||||||
|
|
a, 1 2... n 1 2 |
... k ... 1 2... k ... |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
період |
|
|
|
|
|
|
|
|
||
|
Позначення числових множин |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
Множина натуральних чисел |
|
|
|
|
{1, 2, 3, ..., n, ...} |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
Множина цілих чисел |
|
{..., 2, 1, 0, 1, 2, ...} |
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Множина раціональних чисел |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
m ,n |
|
|
|
||||||||||||||
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
{x | x скінченний або нескінченний |
|
|||||||||||||||||||||
|
|
|
періодичний десятковий дріб} |
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
Множина дійсних чисел |
|
{x | x нескінченний |
|
|
|||||||||||||||||||
|
|
|
|
|
|
десятковий дріб} |
|
|
|
|
||||||||||||||
|
Множина ірраціональних чисел |
|
|
|
|
|
|
|
\ |
|
|
|
|
|||||||||||
|
|
{x | x нескінченний неперіодичний |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
десятковий дріб} |
|
|
|
|
|||||||||||||
|
Включення числових множин. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
7 |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12 Розділ 4. МНОЖИНИ
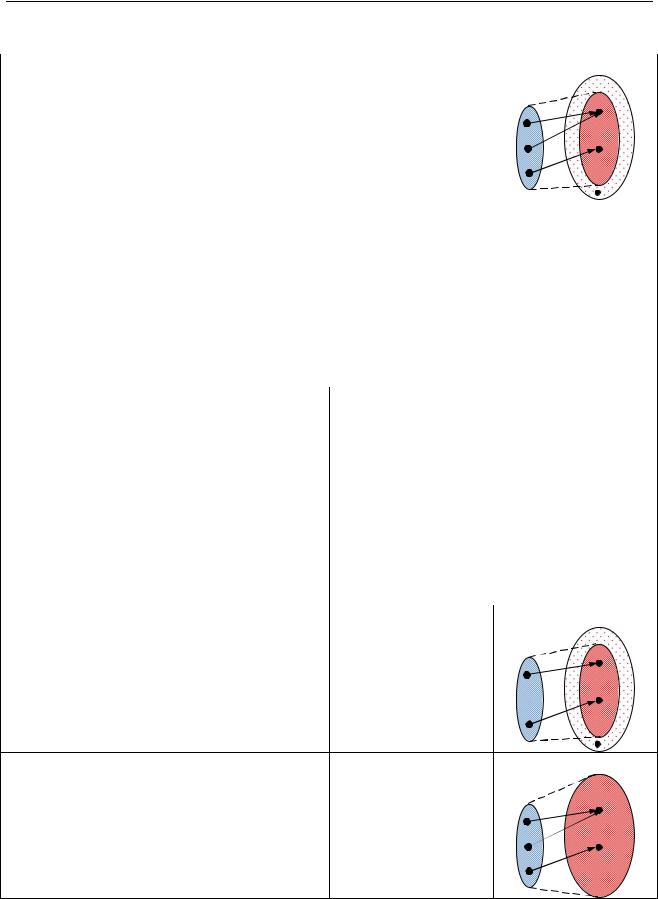
4.7. Відображення множин
Відображення. Відображенням |
|
|
f |
Y |
f : X Y |
|
|
||
множини X у множину Y (функцією з |
X |
|
||
множини X у множину Y ) називають |
|
|
|
|
правило, |
y f (x), x X |
|
|
|
яке кожному елементу x X |
|
|
||
ставить у відповідність |
|
|
|
|
лише один елемент y Y. |
|
|
|
|
аргумент функції |
x (прообраз елемента f (x)) |
|||
|
|
|
||
значення функції |
f (x) (образ елемента x ) |
|
||
|
|
|
|
|
область означення функції |
|
D(f ) X |
|
|
|
|
|||
множина значень функції |
E(f ) {f (x) | x X} f (X) |
|||
|
|
|
|
|
Деякі типи функцій |
|
|
|
|
|
|
|
|
|
дійсна функція |
|
E(f ) |
|
|
|
|
|
|
|
функція дійсного аргументу |
|
D(f ) |
|
|
|
|
|
|
|
дійсна функція кількох змінних |
|
n |
|
|
|
D(f ) , E(f ) |
|
||
вектор-функція |
|
|
n |
|
|
D(f ) , E(f ) |
|
||
послідовність елементів множини Y |
|
f : Y |
|
|
|
|
|
||
числова послідовність |
f : Y |
|
||
|
|
|
|
|
Взаємно однозначне відображення |
x1 X x2 |
X : |
f |
Y |
|
|
|||
(ін’єкція) |
x1 x2 |
|
X |
|
|
|
|||
f (x1 ) f (x2 )
Відображення множини X |
y Y x X : |
f |
Y |
|
|
||
на множину Y |
f(x) y |
X |
|
(сюр’єкція) |
|
|
|
f (X) Y
|
Розділ 4. МНОЖИНИ |
|
13 |
|
|
|
|
|
|
|
|
|
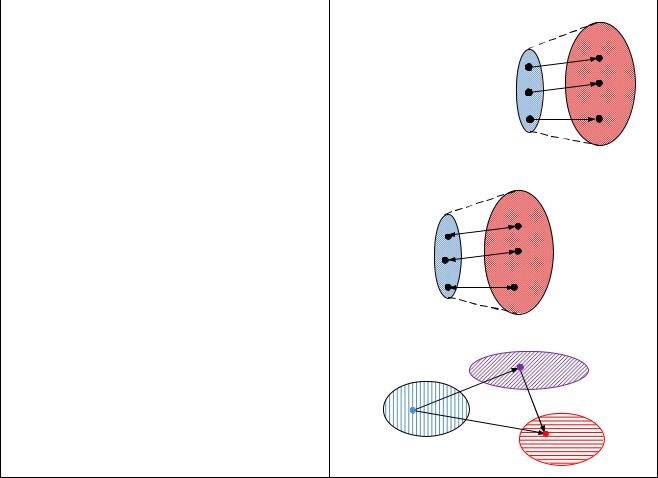
Взаємно однозначна відповідність |
y Y ! x X : |
f |
Y |
|
|
між X та Y |
f(x) y |
X |
|
|
|
(бієкція) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Обернена функція. Якщо |
f |
Y |
|
|
|
відображення f : X Y є бієкцією, |
X |
|
то функцію f 1 : Y X : |
|
|
x f 1(y), y Y |
|
|
|
||
називають оберненою до f функцією. |
|
|
|
||
|
|
|
f 1 |
|
|
|
|
|
|
|
|
Складена функція. Якщо |
|
|
D(f ) |
||
g : D E, |
f : E F, |
D(g) |
g |
g(x) E |
|
то функцію f g : D F : |
|
|
|||
D |
|
f |
|||
(f g)(x) f (g(x)), x D |
x |
|
|||
f g |
F |
||||
називають складеною функцією |
|
||||
|
f(g(x)) |
||||
(суперпозицією функцій f та g). |
|
|
|
||
4.8. Потужність множин
Скінченна множина. Множину A |
Кількість усіх підмножин n -елементної |
називають скінченною, якщо вона має |
скінченної множини дорівнює 2n. |
скінченну кількість елементів. |
|
Рівнопотужні множини. |
Зліченна множина. Множину A |
Множини A та B називають |
називають зліченною, якщо |
рівнопотужними, якщо між їх |
A . |
елементами можна встановити взаємно |
Елементи множини A можна |
однозначну відповідність і позначають |
занумерувати. |
A B. |
|
Властивості скінченних, нескінченних і зліченних множин |
|
|
|
Множина A скінченна тоді й лише |
Нескінченна множина містить |
тоді, коли A {1, 2, ..., n}. |
зліченну підмножину. |
Множина A нескінченна тоді й |
Множини , , — зліченні, |
лише тоді, коли існує множина |
множини , — незліченні. |
B A, B A, така, що A B. |
Декартів добуток зліченних множин |
Нескінченна підмножина зліченної |
є зліченною множиною. |
множини зліченна. |
|

14 Розділ 4. МНОЖИНИ
4.9. Дії з числами. Дроби
Додавання. |
Множення. |
x y z, |
x y z, |
де x, y — доданки, z — сума. |
де x, y — множники, z — добуток. |
Властивості додавання. |
Властивості множення. |
x y y x (комутативність |
x y y x (комутативність |
додавання); |
множення); |
x (y z) (x y) z |
x (y z) (x y) z |
(асоціативність додавання); |
(асоціативність множення); |
x 0 x (існування нуля); |
1 x x (існування одиниці); |
x ( x) 0 (існування |
x x 1 1 (x 0) (існування |
протилежного числа ( x)). |
оберненого числа x 1). |
|
(x y) z x z |
y z (дистрибутивність множення щодо додавання). |
|||||
|
|
|
|
|
|
|
Віднімання. |
|
Ділення. |
|
|
||
x y x ( y) z, |
x : y x y 1 z (y 0). |
|||||
x — зменшуване, y |
— від’ємник, |
x — ділене, y — дільник, z — частка. |
||||
z — різниця. |
|
|||||
|
|
|
|
|||
Правило знаків для множення і ділення |
|
|
||||
|
|
|
|
|
|
|
|
|
: |
: |
|||
|
|
: |
: |
|||
|
|
|
|
|
||
Звичайні дроби |
|
Якщо a b, |
то дріб a називають |
|||
|
x |
|
||||
|
|
|
|
b |
||
|
|
, |
|
правильним, |
|
|
y |
|
|
|
|||
де x — чисельник, |
|
а якщо a b, то — неправильним. |
||||
y 0 — знаменник. |
|
|
|
|
||
Виділення цілої частини |
a bc r |
c r , |
||||
|
|
|
||||
неправильного дробу |
b |
b |
b |
|||
|
|
|
|
|||
|
|
|
|
|
0 r b |
|
Дії з дробами (знаменники всіх дробів відмінні від нуля) |
|
|||||
|
ac |
|
a |
; |
|
|
|
|
|
||||
bc |
|
|
|
|
|
||||||||
|
|
|
b |
|
|
|
|
|
|
||||
|
a |
|
b |
|
|
a b |
; |
|
|
||||
c |
|
|
|
|
|
||||||||
|
|
|
c |
|
|
|
c |
|
|
|
|
||
a |
c |
|
ak |
cl |
ak cl |
, |
|||||||
|
|
b |
|
d |
|
|
|
m |
|
m |
m |
|
|
де m НСК(b,d),k m |
,l m |
; |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
b |
d |
|
|
a |
|
c |
|
|
ac |
|
; |
|
|
|||
b |
|
|
|
|
|
|
|||||||
|
d |
bd |
|
|
|
|
|||||||
|
a |
: |
c |
|
ad |
|
,c 0 |
|
|
||||
b |
|
bc |
|
|
|
||||||||
|
|
d |
|
|
|
|
|
|
|||||
|
|
Розділ 4. МНОЖИНИ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
15 |
|
|||
|
4.10. Відсотки. Пропорції |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Відсотки. Відсоток (процент) |
|
|
1%a |
|
|
a |
|
|
|
|
0, 01a |
|
|
|
||||||||||||
|
числа a — це одна сота частина a. |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
100 |
|
|
|
|||||||||||||||||||||
|
Задачі на відсотки |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
Знаходження відсотків числа |
|
|
|
|
p%a pa |
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
100 |
|
|
|
|
|
|||||
|
Знаходження числа за відсотками |
p%a b a b : |
|
|
p |
b 100 |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
100 |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Знаходження процентного |
число a становить |
a |
|
|
100% від числа b |
|
||||||||||||||||||||
|
відношення чисел |
|
|
|
|||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Якщо число a збільшити на p%, |
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
то дістанемо число |
|
|
|
|
a 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
100 |
|
|
|
|
|||||||||||
|
Якщо число a зменшити на p%, |
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
то дістанемо число |
|
|
|
|
a 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
100 |
|
|
|
|
|||||||||||
|
Формула складених відсотків. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Якщо A — початковий вклад, p — |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
річний відсоток, то наприкінці n -го |
|
|
|
|
A 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
року вклад становитиме |
|
|
|
|
|
|
|
|
100 |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Пропорція. Пропорцією називають |
Властивості пропорції. |
|
|
|
|
|||||||||||||||||||||
|
рівність двох відношень: |
a |
c |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
c |
b |
d |
ad bc; |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
b |
d ,b 0,d 0, |
a |
c |
d |
b |
d c |
; |
|
|
|||||||||||||||||
|
де a,d — крайні члени пропорції; |
|
|
||||||||||||||||||||||||
|
b,c — середні члени пропорції |
b |
d |
|
|
c |
|
|
|
a |
|
|
|
|
|
|
b |
a |
|
|
|
||||||
|
a |
c |
a b c d |
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
b |
d |
|
|
|
b |
|
|
|
|
|
|
|
|
d |
|
|
|
|
||||||
|
Задачі на пропорцію |
a |
c x ad ; |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
x |
d |
|
|
|
|
|
|
c |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
c |
x bc |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
b |
d |
|
|
|
|
|
|
d |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Поділ числа a у відношенні k : l |
|
|
|
|
ak |
та |
|
|
al |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
k l |
|
|
|
|
|
|
k |
l |
|
|
|
|
|||||||||
|
Масова частка речовини. Якщо |
|
xi |
|
|
|
|
|
|
|
|
|
mi |
|
|
|
|
|
|
|
, |
|
|||||
|
суміш містить k речовин масою |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
m1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
m1,m2,...,mk, то масова концентрація |
|
|
|
m2 ... mk |
|
|||||||||||||||||||||
|
|
|
|
|
i |
1, 2,...,k |
|
|
|
|
|||||||||||||||||
|
i -ої речовини |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

16 Розділ 4. МНОЖИНИ
4.11. Подільність натуральних чисел
Ділення націло. Натуральне число |
Ділення з остачею. Якщо a — |
|||||||||||||
a ділиться на натуральне число b |
ділене, b — дільник і |
|
||||||||||||
(позначають a b), якщо існує |
|
|
|
a bc r, |
r b, |
|||||||||
натуральне число c таке, що a bc. |
то кажуть, що c — неповна частка, |
|||||||||||||
Якщо a b, то b — дільник a, |
число a |
r — остача. |
|
|
||||||||||
|
|
|
|
|
||||||||||
кратне b, c |
— частка. |
|
|
|
|
|
|
|
|
|
|
|||
Основні властивості подільності (a, b, c ) |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
0 a; |
|
|
|
|
|
|
|
|
a b, b a a b; |
|
||||
a 1; |
|
|
|
|
|
|
|
|
a b,b c a c; |
|
|
|||
a a; |
|
|
|
|
|
|
|
|
a (bc) a b,a c |
|
||||
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ознаки подільності числа m 1... n 1 n, 1 2 |
... n |
|||||||||||||
m 2 |
|
n {0, 2, 4, 6, 8} |
m 5 |
|
|
n {0, 5} |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
m 3 |
|
|
|
3 |
|
|
m 9 |
|
|
9 |
||||
|
|
|
|
|
|
|
|
|
|
|||||
m 4 |
|
|
|
|
|
|
4 |
m 10 |
|
|
n 0 |
|||
|
|
n 1 |
|
|
||||||||||
|
|
|
|
n |
|
|
|
|
|
|
|
|||
Парні числа. Натуральне число |
Непарні числа. Натуральне число |
|||||||||||||
називають парним, якщо воно ділиться |
називають непарним, якщо воно не |
|||||||||||||
націло на 2. Його можна записати у |
ділиться націло на 2. Його можна |
|||||||||||||
вигляді |
|
|
|
|
|
|
|
|
записати у вигляді |
|
|
|||
|
n 2k, k |
|
|
|
|
|
n 2k 1, k |
|||||||
Прості і складені числа. Простим |
Натуральне число, яке має більше як |
|||||||||||||
числом називають натуральне число, |
два різних дільники, називають |
|||||||||||||
яке має лише два різних дільники — |
складеним. Число 1 не належить ані до |
|||||||||||||
одиницю і саме число. |
|
|
|
|
|
простих, ані до складених. |
||||||||
Основна теорема подільності. |
|
|
|
|
|
|||||||||
Будь-яке натуральне число, більше за |
|
a p 1 p 2 |
...p k , |
|||||||||||
одиницю, можна розкласти в добуток |
1 |
|
2 |
k |
||||||||||
де pi — прості числа, i . |
||||||||||||||
простих чисел, причому цей добуток |
||||||||||||||
єдиний з точністю до порядку |
|
|
|
|
|
|
|
|||||||
співмножників. |
|
|
|
|
|
|
|
|
|
|
||||
Найбільший спільний дільник. |
Найменше спільне кратне. |
|||||||||||||
Найбільшим спільним дільником |
|
|
Найменшим спільним кратним |
|||||||||||
натуральних чисел a та b називають |
натуральних чисел a та b називають |
|||||||||||||
найбільше число, на яке ділиться і |
найменше число, яке ділиться як на |
|||||||||||||
число a, і число b і позначають |
|
|
число a, так і на число b, і позначають |
|||||||||||
|
НСД(a,b). |
|
|
|
|
|
|
НСК(a,b). |
||||||
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
НСД (a,b) НСК(a,b) ab |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

|
Розділ 4. МНОЖИНИ |
17 |
|
|
|
|
|
|
|
|
Алгоритм знаходження НСД. |
Алгоритм знаходження НСК. |
|
|
|
Розкладають задані числа на прості |
Розкладають задані числа на прості |
|
|
|
множники. |
множники. |
|
|
|
Складають добуток зі спільних |
Складають добуток з усіх простих |
|
|
|
простих множників, узятих з |
множників, узятих з найбільшим |
|
|
|
найменшим показником степеня. |
показником степеня. |
|
|
4.12. Деякі спеціальні нерівності
Порівняння дійсних чисел. Для |
a b (a дорівнює b); |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
будь-яких дійсних чисел a та b |
a b (a менше за b, |
|
b більше за a) |
|||||||||||||||||||||||||||||||||||
встановлено одне з трьох відношень: |
a b (a більше за b, |
|
b менше за a) |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
Властивості рівностей. |
Властивості нерівностей. |
|
|
|
|
|
||||||||||||||||||||||||||||||||
Якщо a b,b c, то a c. |
Якщо a b,b c, |
то a c. |
||||||||||||||||||||||||||||||||||||
Якщо a b, то: |
Якщо a b, то: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
a c b c; |
a c b c; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
ac bc; |
|
ac bc,c 0 |
і ac bc, c 0; |
|||||||||||||||||||||||||||||||||||
|
a |
|
b |
, c 0 |
|
a |
|
b |
, c 0 |
і |
|
a |
|
|
|
b |
|
, c 0 |
||||||||||||||||||||
c |
|
|
|
|
c |
|
|
|
||||||||||||||||||||||||||||||
|
c |
|
c |
|
c |
|
|
|
|
|
|
|
|
|
|
|
|
c |
|
|
|
|
|
|
|
|
|
|||||||||||
Нерівність Бернуллі |
|
|
|
|
n |
|
1 nh (h 1, n ) |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
(1 h) |
|
|||||||||||||||||||||||||||||||
Середнє арифметичне |
|
|
|
|
A |
|
a1 |
a2 |
... an |
|||||||||||||||||||||||||||||
чисел a1,a2,...,an |
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
Середнє геометричне |
|
|
|
|
|
|
|
G |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
n a a |
...a |
|
|
|
|
|
|
|
||||||||||||||||||||||
чисел a1,a2,...,an |
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
1 |
|
2 |
|
|
|
n |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Середнє гармонічне |
|
|
|
Hn |
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
чисел a1,a2,...,an |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
1 |
|
|
|
|
1 |
|
... |
|
1 |
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
a |
2 |
|
a |
n |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Середнє квадратичне |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
a2 |
a2 |
... a2 |
|||||||||||||||||||||||||||
чисел a ,a ,...,a |
|
|
|
Sn |
|
|
1 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
n |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
1 2 |
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Співвідношення між середніми |
|
|
Hn Gn |
An |
Sn |
(ai 0) |
||||||||||||||||||||||||||||||||
Нерівність Коші |
|
|
|
|
|
|
|
|
|
a1 |
|
a2 |
... an |
|||||||||||||||||||||||||
|
|
n a a |
...a |
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
1 2 |
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
||||
(ai 0)
18 Розділ 4. МНОЖИНИ
4.13. Числова вісь
Модуль дійсного числа. Модулем |
|
|
|
|
|
x 0, |
|
||||||||||||
|
|
|
|
x, |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|||
(абсолютною величиною) дійсного |
|
|
|
x 0 |
|
||||||||||||||
|
|
|
|
x, |
|
||||||||||||||
числа x називають число |
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|||||||||||||
Нескінченності. Множину дійсних |
1) x ( ) , |
|
|
||||||||||||||||
чисел доповнюють елементами, які |
x ( ) x ; |
|
|||||||||||||||||
називають |
|
|
|
|
2) x( ) , |
|
|
||||||||||||
плюс нескінченністю |
|
|
|||||||||||||||||
x( ) x 0; |
|
||||||||||||||||||
та мінус нескінченністю |
|
||||||||||||||||||
і позначають та , |
3) ( ) ( ) , |
|
|||||||||||||||||
вважаючи при цьому, що: |
( ) ( ) ; |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
4) x x |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Числова вісь. Числовою віссю |
|
O |
1 |
|
E |
|
|||||||||||||
називають пряму, на якій вибрано: |
|
|
|
|
|||||||||||||||
0 |
|
|
|
1 |
x |
||||||||||||||
1) початок — точку O; |
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||
2) додатний напрям; |
Між точками числової осі і множиною |
||||||||||||||||||
дійсних чисел можна встановити |
|||||||||||||||||||
3) масштаб. |
|
|
|
|
|||||||||||||||
|
|
|
|
взаємно однозначну відповідність. |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||
Правило зображення дійсного числа |
|
|
|
|
|
|
|
|
|
||||||||||
xM точкою числової осі M : |
|
O |
|
|
|
|
M |
|
|||||||||||
1) |
|
OM |
|
|
|
xM |
|
; |
|
|
|
|
|
x |
|||||
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
2) якщо x |
M |
|
0, то точка M |
|
|
|
|
|
xM |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
розташована ліворуч від точки O, |
M2 |
|
O |
M1 |
|
||||||||||||||
якщо x |
M |
|
0, то точка M O; |
x2 0 |
|
0 |
|
x1 0 |
x |
||||||||||
якщо xM 0, то точка M |
Число x називають координатою |
||||||||||||||||||
розташована праворуч від точки O. |
точки M на числовій осі і позначають |
||||||||||||||||||
M(x). |
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
||||||||||||
Віддаль між точками. Віддаль між |
M1 |
|
|
|
|
M2 |
|
||||||||||||
точками M1(x1) та M2(x2) на прямій |
x1 |
|
|
|
|
x2 |
x |
||||||||||||
знаходять за формулою |
|
|
|
|
x2 x1 |
|
|
||||||||||||
|
|
|
|
|
|
||||||||||||||
d(M1, M2 ) x2 x1 .
|
|
|
|
|
|
|
|
|
|
|
|
|
Розділ 4. МНОЖИНИ |
|
|
|
|
|
|
|
19 |
|
|||||
|
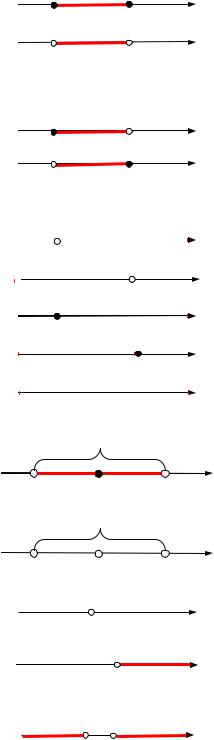
4.14. Числові проміжки |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Відрізок [a;b] {x | a x b} |
|
|
|
|
a |
b |
x |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Інтервал (a;b) {x | a x b} |
|
|
|
|
a |
b |
x |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Півінтервали |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
[a;b) {x | a x b} |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
b |
x |
|
||||||
|
(a;b] {x | a x b} |
|
|
|
|
a |
b |
x |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Нескінченні проміжки |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(a; ) {x | a x} |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
a |
|
|
|
|
x |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( ;b) {x | x b} |
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
||||||||||||
|
|
|
|
|
|
|
|
b |
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
[a; ) {x | a x} |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
a |
|
|
|
|
x |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( ;b] {x | x b} |
|
|
|
|
|
|
|
|
|
|
|
x |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
b |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( ; ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
-окіл точки a . |
|
|
|
|
|
U |
(a) |
|
|
|
||||||||||||||||
|
U (a) {x |
|
|
|
|
x a |
} |
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
(a ;a ), 0 |
a |
|
|
a |
|
|
a |
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
Проколений -окіл точки a . |
|
|
|
|
|
U |
(a) |
|
|
|
||||||||||||||||
|
U (a) \ {a} {x |
|
0 |
x a |
} |
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
(a ;a) (a;a ) |
a |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
a |
|
|
a |
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
-окіл точки |
|
|
|
|
U ( ) |
|
|
|
||||||||||||||||||
|
U ( ) {x |
x } ( ; ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
-окіл точки |
|
|
|
|
|
|
|
U ( ) |
|
|
|
|||||||||||||||
|
U ( ) {x |
|
|
|
x } ( ; ) |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
-окіл точки |
|
|
|
|
|
U ( ) |
|
|
|
|||||||||||||||||
|
U ( ) x |
|
|
x |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
( ; ) ( ; ) |
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

20 Розділ 4. МНОЖИНИ
4.15. Елементи комбінаторики
Факторіал |
|
|
|
n ! 1 2 ... n; 0 ! 1 |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
(n 1)! n !(n 1) |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Подвійний факторіал |
|
|
|
|
|
(2k)!! |
2 4 ... (2k) |
|
|
||||||||||
|
|
|
(2k 1)!! 1 3 ... (2k 1) |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Розміщення. Розміщенням з n |
|
|
|
|
|
Кількість розміщень |
|
|
|||||||||||
елементів по k |
елементів (0 k n) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
без повторення |
|
з повтореннями |
|||||||||||||||||
називають будь-який упорядкований |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
n ! |
|
|
|
k |
|
n |
k |
||||||
набір з k елементів n -елементної |
k |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
An |
|
|
|
|||||||||||
множини. |
|
An |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
(n |
k)! |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Розміщення різняться одне від одного |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
або складом елементів або порядком їх |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
розташування. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Перестановка. Перестановкою з n |
|
|
|
Кількість перестановок |
|
|
|||||||||||||
елементів (без повторень) називають |
|
|
|
|
(n1 n2 ... nk |
n) |
|
|
|||||||||||
будь-яку впорядковану підмножину з |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
без повторення |
|
з повтореннями |
|||||||||||||||||
n елементів заданої множини. |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Перестановки різняться одне від |
Pn |
|
|
n ! |
|
Pn(n1, n2, ..., nk ) |
|||||||||||||
одного лише порядком розташування |
|
|
|
|
|
|
|
|
|
|
|
|
n ! |
|
|
||||
елементів. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
n !n |
2 |
!...n ! |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
k |
||||
Комбінація. Комбінацією з n |
|
|
|
|
|
Кількість комбінацій |
|
|
|||||||||||
елементів по k |
елементів (0 k n) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
без повторення |
|
з повтореннями |
|||||||||||||||||
називають будь-який набір з k |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
елементів n -елементної множини. |
|
|
|
|
|
|
n ! |
|
|
k |
|
|
k |
|
|
||||
|
|
|
k |
|
|
|
|
|
|
|
|
Cn |
Cn k 1 |
||||||
Комбінації різняться одна від одної |
Cn |
(n k)!k ! |
|||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||
лише складом елементів. |
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Правило суми. Якщо об’єкт a |
Правило добутку. Якщо об’єкт a |
||||||||||||||||||
можна вибрати m способами, а об’єкт |
можна вибрати m способами і після |
||||||||||||||||||
b — іншими n способами, то вибір |
кожного з таких виборів об’єкт b |
|
|
||||||||||||||||
«або a, або b » можна здійснити |
можна вибрати n способами, то вибір |
||||||||||||||||||
m n способами. |
«a та b » (у вказаному порядку) можна |
||||||||||||||||||
|
|
|
здійснити mn способами. |
|
|
|
|
|
|||||||||||
Властивості Ak . |
Властивості Ck . |
|
|
|
|
|
|||||||||||||
|
|
n |
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|||
An |
An 1 |
P n !; |
Ck |
|
Cn k, k 0, 1, ..., n; |
|
|
|
|||||||||||
n |
n |
n |
n |
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
||
A0 |
1; |
|
Cn0 Cnn 1; |
|
|
|
|
|
|
|
|
||||||||
n |
|
|
Cnk 11 |
|
Cnk Cnk 1, k 0,1,..., n 1; |
||||||||||||||
Ak 1 (n k)Ak |
|
||||||||||||||||||
n |
|
n |
|
Cn1 ... Cnn 1 Cnn 2n |
|||||||||||||||
|
|
|
Cn0 |
||||||||||||||||
