2. Формирование закона управления, обеспечивающего желаемые значения корней характеристического уравнения

Структурная схема типового объекта в отсутствие возмущающего воздействия имеет вид

Математическое описание объекта, полученное в результате поэлементного описания, имеет вид:

(2.1)

В матричной форме систему (2.1) можно представить в виде

, (2.2)

здесь ,,,.

Передаточная функция объекта имеет вид

(2.3).

Выбор переменных состояния не является единственно возможным. Переменные состояния могут быть выбраны множеством способов. Любая замена векторана вектор

, (2.4)

где- неособая матрицаприводит к новому матричному уравнению

, (2.5)

где . (2.6)

Выберем переменные состояния так, чтобы в системе (2.5) матрица соответствовала системе дифференциальных уравнений, записанной в первой нормальной форме Коши, т.е., чтобы матрицаимела вид

. (2.7)

Для этого от передаточной функции (2.3) перейдем к дифференциальному уравнению объекта

,

здесь или

, (2.8)

. Заметим, что характеристическое уравнение объекта, соответствующее передаточной функции (2.3) и дифференциальному уравнению (2.8), имеет вид

или

(здесь). (2.9)

Выберем переменные состояния следующим образом:

.

При выбранных переменных система дифференциальных уравнений объекта примет вид

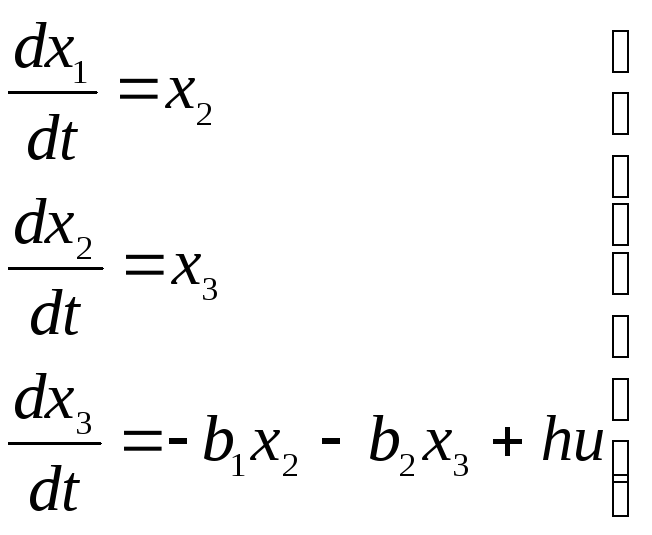(2.10).

При этом матричное уравнение (2.5) имеет матрицы

,,.

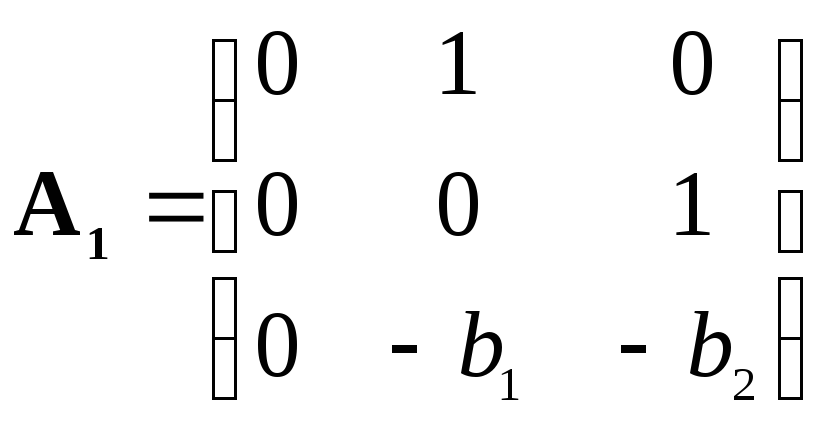Сформируем управление :

(2.11)

так, чтобы замкнутая система имела заранее заданные корни характеристического уравнения.

Имеем для замкнутой системы

,

,

и тогда, исключая второе уравнение, получим матричное уравнение замкнутой системы

.

Рассмотрим собственную матрицу замкнутой системы . Имеем

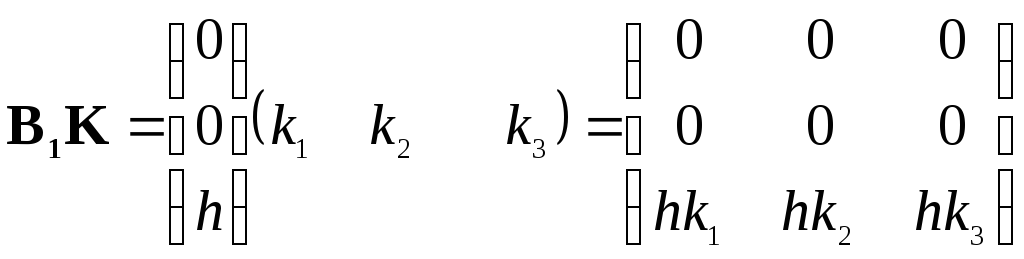и тогда

. (2.12)

Пусть желаемые корни (в общем случае комплексно-сопряженные) равны . Тогда по теореме Виета характеристическое уравнение может быть представлено в виде

, (2.13)

здесь определяются по заданным значениям. Таким образом, необходимо, чтобы характеристическое уравнение замкнутой системы имело заданные коэффициенты. Рассмотрим вопрос, как связаны коэффициентыс элементами матрицы (2.12). Сравнивая вид матрицы(2.7) с характеристическим уравнением (2.9), можно видеть, что элементы последней строки матрицыявляются коэффициентами характеристического уравнения Применяя этот результат к матрице синтезированной системы (11) и характеристическому уравнению (2.13), получим

,

откуда значения коэффициентов, задающих требуемый закон управления определятся зависимостями

. (2.14)

Зависимости (2.14) определяют коэффициенты обратных связей по переменным состояния в базисе . Для окончательного решения задачи необходимо пересчитать эти коэффициенты для базиса.

Имеем ,,

,,

откуда следует, что

,. (2.15)

Для того, чтобы получить аналогичную зависимость для переменной рассмотрим второе уравнение системы (2.1)

.

Приведем его к виду

. (2.16)

Так как и, следовательно, то из (2.16) получим

и

. (2.17)

Подставляя (2.15), (2.17) в уравнение, определяющее управление (2.11), получим

(2.18)

где ,,.

3.Расчет переходного процесса синтезированной сау

Математическое описание синтезированной системы состоит из системы уравнений разомкнутого объекта (2.1) и уравнения (2.18). Расчет переходного процесса на единичное ступенчатое входное воздействие имеет целью проверку выполнения предъявляемых к системе требований по времени регулирования и перерегулированию. Он может проводиться либо непосредственным численным интегрированием системы уравнений (2.1), (2.18) либо посредством определения с помощью этих уравнений передаточной функции замкнутой синтезированной системы, определением аналитического выражения для переходного процесса и его расчетом по полученной формуле.

Литература

1.В.А. Бесекерский, Е.П. Попов. Теория систем автоматического регулирования. -М.: Наука, 1975.- 768с.

2. Д.В. Васильев, В.Г. Чуич. Системы автоматического управления (примеры расчета).- М.: Высшая школа, 1967.- 418с.

3. Н.Н. Иващенко Автоматическое регулирование.- 4 изд.- учебник для вузов.- М.: машиностроение, 1976.- 736с.

4. Техническая кибернетика. Устройства и элементы систем автоматического регулирования. Кн.1/ Под ред. В.В. Солодовникова.- М.: Машиностроение, 1973.- 680с.

5. Ю.И. Топчеев, А.П. Цыпляков. Задачи по теории автоматического регулирования. учебное пособие для вузов.- М.: Машиностроение, 1977.- 592с.

6. Техническая кибернетика. Теория автоматического регулирования. Кн.2/ Под ред. В.В. Солодовникова.- М.: Машиностроение, 1967.- 682с.

Рассмотрено за заседании

кафедры САУ. Протокол № 6

от 28.02.02

Заведующий кафедрой Н.В. Фалдин