
Fizika_Laboratornye_raboty / 6
.pdfКАЗАНСКАЯ ГОСУДАРСТВЕННАЯ АРХИТЕКТУРНО-СТРОИТЕЛЬНАЯ АКАДЕМИЯ
_________________________________________________________
Кафедра физики
МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ЛАБОРАТОРНЫМ РАБОТАМ ПО ФИЗИКЕ
для студентов специальностей
2903, 2906, 2907, 2908, 2910
Лабораторная работа № 6
ОПРЕДЕЛЕНИЕ МОМЕНТА ИНЕРЦИИ ДИСКА МЕТОДОМ ВРАЩЕНИЯ
Казань - 1997
Составитель: В.И. Сундуков Под редакцией В.В. Алексеева, Л.И. Маклакова
УДК 539.15
Методические указания к лабораторным работам по физике для студентов дневного и заочного отделений специальностей 2903, 2906, 2907, 2908, 2910/ Казанская государственная архитектурно-строитель-ная академия; Сост. В.И. Сундуков. Под редакцией В.В. Алексеева, Л.И. Маклакова. Казань, 1997 г.
10с.
Вработе рассматриваются общие вопросы вращательного движения. При- водятся теоретический и практический способы определения моментов инер- ции диска.
Ил. 3. Табл. 1.
Рецензент профессор кафедры молекулярной физики Казанского госуни- верситета Скирда В.Д.
ãКазанская государственная архитектурно-строительная академия, 1997 г.
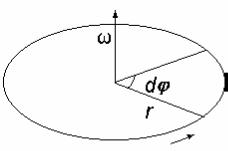
ЭЛЕМЕНТЫ КИНЕМАТИКИ ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ
Твердым телом называется совокупность точек, расстояния между кото- рыми в процессе движения не меняются. Любое движение твердого тела может быть представлено в виде поступательного и вращательного. При поступа- тельном движении все точки твердого тела движутся с одинаковыми линейны- ми скоростью и ускорением. При вращательном движении точки твердого тела двигаются по окружностям, центры которых лежат на одной и той же прямой, называемой осью вращения. Точки расположенные на разных расстояниях от оси вращения обладают различными линейными скоростями и ускорениями, так как движутся по окружностям различной длины. Поэтому для характери- стики вращательно движения твердого тела необходимо ввести такие величи- ны, которые будут одинаковыми для всех его точек. Такими величинами явля- ются угол поворота, угловая скорость и угловое ускорение.
Рассмотрим определение этих величин и их |
|
|
связь с линейными величинами на примере дви- |
|
|
жения по окружности материальной точки. Дви- |
|
|
жение точки будем описывать углом поворота |
|
|
радиуса-вектора, проведенного в рассматривае- |
|
|
мую точку из центра окружности (рис.1). Удобно |
|
|
угол поворота ϕ считать вектором, который сов- |
Рис. 1 |
|
падает с осью вращения. Его направление нахо- |
||
|
дится по правилу правого винта. Модуль вектора ϕ выбирается равным углу поворота. Введение угла поворота в форме вектора позволяет одновременно характеризовать ось вращения и направление движения.Такие вектора называ- ются аксиальными, и они в отличие от обычных (полярных векторов) не имеют точки приложения. Для характеристики быстроты вращения вводится угловая
скорость ω. Вектор угловой скорости направлен вдоль оси вращения по прави- лу правого винта. Модуль вектора угловой скорости равен производной от угла
поворота по времени
ω = |
dϕ |
. |
(1) |
|
|||
|
dt |
|
|
Если угловая скорость постоянна, то вращение называется равномерным. Для
характеристики быстроты изменения угловой скорости вводится понятие углового ускорения, равного производной от угловой скорости по времени
ε = |
dω |
. |
(2) |
|
|||
|
dt |
|
|
Вектор углового ускорения совпадает по направлению с вектором угловой ско- рости при ускоренном вращательном движении и противоположен ему при за- медленном вращении.
Линейная скорость точки V направлена по касательной к окружности. Мо-
дуль вектора V равен производной от пути по времени
V = |
ds |
. |
(3) |
|
|||
|
dt |
|
|
Быстроту изменения линейной скорости по модулю характеризует танген-
циальное ускорение
a |
= |
dV |
, |
(4) |
|
||||
τ |
|
dt |
|
|
|
|
|
|
а быстроту изменения скорости по направлению − нормальное ускорение
an = |
V 2 |
. |
(5) |
|
R |
||||
|
|
|
Тангенциальное ускорение направлено по касательной к окружности, а нор- мальное − по радиусу к центру окружности. Линейные и угловые характери- стики движения вращающегося тела связаны между собой. Учитывая, что s = R ×ϕ, получаем
V = |
ds |
= R × |
dϕ |
= ω × R . |
(6) |
|
dt |
dt |
|||||
|
|
|
|
Связь между тангенциальным и угловым ускорениями можно определить, если продифференцировать соотношение (6) по времени:
a |
= |
dV |
|
= |
d |
(ω × R) = R × |
dω |
= ε × R . |
(7) |
|
|
|
|
|
|||||||
τ |
|
|
dt |
|
dt |
dt |
|
|||
Подставляя V = ω × R в формулу (5) получим соотношение между нор- |
||||||||||
мальным ускорением и угловой скоростью |
|
|||||||||
αn = |
V 2 |
= ω 2 × R. |
|
|
(8) |
|||||
|
R |
|
|
|||||||
|
|
|
|
|
|
|
|
|
||
ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА
Чтобы твердое тело с закрепленной осью привести во вращение, необхо- димо к какой-то его точке приложить внешнюю силу F, не проходящую через ось вращения и не параллельную ей. Рассмотрим случай когда сила F лежит в плоскости, перпендикулярной оси вращения (рис. 2). Из опыта следует, что вращающие действие силы тем значительнее, чем больше расстояние между прямой, вдоль которой эта сила действует, и осью вращения. Это расстояние равно длине перпендикуляра опущенного из центра вращения на прямую, вдоль которой направлена действующая сила. И это расстояние называется плечом l
(l = r × sinα ).
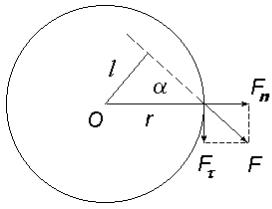
Способность силы вращать тело зависит не только от величины силы, но
и от ее направления действия и точки приложения к твердому телу. Момен-
том силы относительно оси вращения называется векторная величина, харак-
теризующая вращательную способность силы. Ее модуль равен произведению модуля силы на плечо: M = F × l или
M = F × r × sinα = F × r |
Рис. 2(9) |
τ |
|
где Fτ - проекция силы F на касательную к траектории движения.
Вектор M направлен по оси вращения в сторону поступательного движения правого винта, если его вращать в направлении действия силы. Если на тело действует несколько сил, то результирующий момент сил равен сумме момен-
тов каждой силы с учетом направления действия
M = åMi . |
(10) |
i
Рассмотрим вывод основного закона динамики вращения твердого тела. Разобъем твердое тело мысленно на частицы с массой Dmi , которые будем
рассматривать как материальные точки. Движение каждой такой частицы будет
подчиняться второму закону Ньютона
a = |
Fi |
, |
(11) |
|
|||
i |
Dmi |
|
|
|
|
|
где Fi – векторная сумма всех внешних и внутренних сил, приложенных к час- тице. Разложим силу Fi на две составляющие — касательную к траектории
движения Fτi и перпендикулярную к ней Fni (рис. 2). Так как сила Fni не приво- дит тело во вращательное движение (момент силы равен нулю), то запишем уравнение движения только для проекции ускорения ai и силыFτi на направле- ние касательной к траектории:
a |
= |
Fτi |
. |
(12) |
|
||||
τi |
|
Dmi |
|
|
|
|
|
||
Умножим числитель и знаменатель этого равенства на радиус вращения i- час-
тицы
ri: a |
= |
Fτi × ri |
. |
(13) |
|
||||
τi |
|
Dmi × ri |
|
|
|
|
|
||
Переходя к угловому ускорению согласно выражению(7) запишем, учитывая соотношение (9):
ε = |
Mi |
|
|
|
. |
(14) |
|
Dm × r 2 |
|||
|
i i |
|
|
Величина, равная произведению массы материальной точки на квадрат ее рас- стояниядо оси вращения, называется моментом инерции материальной точки:
I |
i |
= Dm × r 2 . |
(15) |
|
i i |
|
|
Тогда равенство (10) можно записать в виде: |
|
||
ε = Mi . |
(16) |
||
|
|
Ii |
|
Из этого соотношения вытекает, что чем больше Ii, тем меньше ε, т.е., момент
инерции характеризует способность материальной точки противодействовать изменению ее угловой скорости. Такое свойство в механике называется инерт- ностью. Таким образом, момент инерции, подобно массе в поступательном движении, служит мерой инертности тела во вращательном движении. Момент инерции величина скалярная и обладает свойством аддитивности, т.е., момент инерции твердого тела равен сумме моментов инерции составляющих его час- тиц:
I = åIi . |
(17) |
Продолжим вывод закона и просуммируем соотношение (16) по всем матери- альным частицам, учитывая то, что для всех точек угловая скорость одинакова:
åMi
ε = |
i |
(18) |
|
åIi |
|||
|
|
i
Согласно соотношений (10) и (17) выражение (18) записывается в векторной
форме как
r |
M |
|
ε = |
|
(19) |
I |
Это выражение называется основным законом динамики вращения твердого тела. Угловое ускорение твердого тела прямо пропорционально результирую- щему моменту внешних сил, приложенных к телу, обратно пропорционально моменту инерции и направлено в сторону действия момента сил.
РАБОТА ПРИ ВРАЩАТЕЛЬНОМ ДВИЖЕНИИ
Если к телу приложена сила F и под ее действием происходит элемен- тарное перемещение ds, то для элементарной работы dA справедливо соотно- шение:

dA = Fτ × ds , |
(20) |
где Fτ – проекция силы F на направление движения. Так как ds = r × dϕ и
Fτ × r = M , то можно записать: |
|
dA = Fτ × r ×dϕ = M × dϕ . |
(21) |
Если момент силы M = const, то |
|
A = M ×ϕ |
(22) |
ОПИСАНИЕ УСТАНОВКИ И ВЫВОД ЗАБОЧЕЙ ФОРМУЛЫ
Цель работы − применение законов динамики поступательного и враща- тельного движения для определения момента инерции диска.
Экспериментальная установка состоит из диска А со шкивом Б, на который наматывается нить с прикрепленным к ней грузом m. Диск может вращаться вокруг оси О. Высота перемещения груза определяется по вертикально распо- ложенной линейке (рис. 3).
Груз массой m движется вниз с постоянным ускорением a под действием двух сил. Сила тяжести mg направлена вниз, а сила натяжения нити T направ- лена вверх. Cилой сопротивления воздуха пренебрегаем. По второму закону Ньютона:
mg - T = ma . |
(23) |
Вращение диска происходит под дейст- вием момента силы натяжения нити T×r и мо- мента силы трения Mt, тормозящего враще- ние. По основному закону динамики враща- тельного движения:
T × r - Mt = I ×ε (24)
где r − радиус шкива, ε − угловое ускорение диска, I − момент инерции диска. Так как точки шкива, на который намотана нить дви-
жутся с тангенциальным ускорением равным ускорению груза a, то. a = ε × r Из формул (23) и (24) получим выражение для момента инерции диска:
Рис. 3
I = |
[m(g - a)× r - Mt ]× r |
. |
(25) |
|
|||
|
a |
|
|
Для нахождения Mt воспользуемся законом сохранения энергии. Груз, поднятый на высоту h1 обладает потенциальной энергией mgh1. При опускании
груза вниз его потенциальная энергия переходит в основном в кинетическую энергию вращательного движения диска. После опускания груза его потенци- альная энергия обращается в нуль, а кинетическая энергия вращения диска принимает максимальное значение. Диск продолжает вращаться, наматывая нить на шкив. За счет кинетической энергии вращающегося диска груз подни- мается на высоту h2 . В верхнем положении груза кинетическая энергия диска обращается в нуль, а потенциальная энергия груза принимает максимальное значение. Высота h2 будет меньше первоначальной высоты h1 из-за потери энергии на трение. По закону сохранения энергии убыль потенциальной энер- гии будет равна работе момента силы трения, возникающего при вращении диска:
mgh1 - mgh2 = Mt ×ϕ . |
(26) |
Так как путь проходимый какой-либо точкой на поверхности шкива, на ко- торый намотана нить, равен пути проходимому грузом h1 + h2 , то результи- рующий угол поворота будет равен:
ϕ = |
h1 + h2 |
. |
|
|
(27) |
|
|
|
|||||
|
r |
|
|
|
|
|
Подставляя выражение (27) в (26) получим: |
|
|||||
Mt = mgr( h1 - h2 ) . |
|
(28) |
||||
|
|
h1 + h2 |
|
|
||
С учетом последнего выражения формулу (25) можно записать в следую- |
||||||
щем виде: |
|
|
|
|
|
|
I = mr2 é |
|
2gh2 |
|
-1ù |
(29) |
|
|
|
|||||
|
êa( h + h ) |
ú |
|
|||
ë |
1 2 |
|
û |
|
||
Движение груза на нити из начального положения является равноускорен- ным без начальной скорости. Для пути груза вниз и для ускорения справедливы
следующие выражения: h = |
at2 |
и a = |
2h |
|
|
1 |
(t − время движения груза вниз). |
||
|
|
|||
1 |
2 |
|
t2 |
|
|
|
|||
Подставив в формулу (23) выражения для ускорения поступательного движе- ния a, получим конечную формулу для расчета момента инерции диска:
I = mr2 |
é |
gh t2 |
ù |
|
|
ê |
2 |
|
-1ú |
(30) |
|
|
|
||||
|
êh1( h1 + h2 ) |
ú |
|
||
|
ë |
|
|
û |
|
Порядок выполнения работы
1.Внимательно прочитать пункты выполнения задания и изучить рабо- чую формулу (30).
2.Измерить штангенциркулем диаметр шкива и определить его радиус r.
3.Отметить по линейке нижнее положение груза (по верхнему или ниж- нему краю).
4.Поднять груз наматывая на шкив нить в верхнее положение, опреде- лить высоту h1 относительно выбранного нижнего положения.
5.Отпустив диск измерить секундомером время движения груза до ниж- ней точки t. Позволить диску продолжать по инерции вращаться и за- фиксировать верхнюю точку подъема груза h2.
6.Данные занести в таблицу. Значение массы груза указано на установке.
7.Рассчитать по формуле (30) момент инерции диска.
8.Повторить опыт (пункты 4-7) несколько раз, рассчитать среднее значе- ние момента инерции и определить погрешность измерений.
|
|
|
|
|
|
Таблица 1 |
|
|
|
|
|
|
|
|
|
N опыта |
r, м |
h1, м |
h2, м |
t, с |
I, кг×м2 |
|
Icp, кг×м2 |
1 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
КОНТРОЛЬНЫЕ ВОПРОСЫ
1.Что характеризуют и как направлены угловая скорость, угловое ускорение?
2.Какова связь между линейными и угловыми кинематическими величинами?
3.Что называется моментом силы?
4.Дайте понятие момента инерции.
5.Сформулируйте основной закон динамики вращательного движения.
6.Выведите основной закон динамики вращательного движения.
7.Выведите рабочую формулу.
8.Какое значение момента инерции диска будет получено ( завышенное или за- ниженное) если при выводе рабочей формулы не учитывать потери энергии на трение.
