
физика механика
.pdf
Движение тела, траектория которого – произвольная, не прямая, линия.
● Длина пути
Сумма длин всех участков траектории, пройденных телом за рассматриваемый промежуток времени.
●Поступательное движение абсолютно твердого тела8
Движение, при котором любая прямая, связанная с телом, перемещается параллельно самой себе. При поступательном движении траектории всех точек тела одинаковы, скорости
иускорения всех точек в данный момент времени равны. Поэтому для описания такого движения тела достаточно описать движение одной произвольной его точки,
называемой материальной.
●Материальная точка (МТ)
Тело, размерами которого можно пренебречь в условиях данной задачи.
Критерий: тело можно считать материальной точкой, если его размеры, по крайней мере, на порядок (в 10 раз) меньше характерных размеров, используемых в задаче.
***** Глава1. §1 *****
§2. Общий вид задания движения МТ
Независимо от вида траектории и выбранной системы отсчета описание движения материальной точки сводится к заданию закона ее движения.
● Закон движения
Зависимость радиус-вектора r или координат x, y, z точки
от времени t, которая определяет ее положение при движении в любой момент времени:
(1.1) r = r (t) x = x(t), y = y(t), z = z(t).
Векторный r = rr(t) и координатный x=x(t), y=y(t), z=z(t) способы задания движения равносильны ( ).
8Абсолютно твердое тело – тело, расстояния между частицами которого не изменяются
-21 -
● Радиус-вектор точки rr(t)
Вектор, проведенный из начала координат системы отсчета в местонахождение исследуемой точки.
● Перемещение r
Вектор, соединяющий начальное и конечное положения исследуемой точки:
r = rr(t + t) − rr(t).
Зная закон движения и начальные условия МТ (положение и скорость в момент времени t = t0 ) можно решить основную задачу
механики, то есть определить положение тела в любой момент времени.
***** Глава1. §2 *****
§3. Количественные характеристики движения материальной точки
Описание движения материальной точки сводится к
математическому |
представлению в |
явном виде радиус-вектора |
||||||
r = r (t), скорости υ =υ(t) и ускорения a = a(t). |
|
|
|
|||||
● Средняя скорость υr |
|
|
|
|
|
|||
Вектор, равный отношению приращения радиус-вектора |
r |
|||||||
точки |
к промежутку времени |
t, в |
течение которого |
это |
||||
приращение произошло: |
|
|
|
|
|
|||
(1.2) |
υr = |
r |
υx = |
x , υy |
= |
y , υz = |
z . |
|
|
|
t |
|
t |
|
t |
t |
|
● Мгновенная скорость υr
Вектор, равный пределу средней скорости при неограниченном уменьшении промежутка времени, в течение которого рассматривается движение точки, то есть первой производной радиус-вектора точки по времени:
(1.3) υr = lim |
υr = lim |
r |
= dr |
|
t →0 |
t→0 |
t |
dt |
|
|
- 22 - |
|
|
|
|
|
|
υx |
= lim |
|
υx = lim |
|||
|
|
t→0 |
|
t →0 |
|
|
|
|
|
(1.3′) |
υy = lim |
υy |
= lim |
|
|
|
t→0 |
|
t →0 |
|
|
|
υz |
= lim |
|
υz = lim |
|||
|
|
t→0 |
|
t →0 |
xt = dxdt , yt = dydt , zt = dzdt .
● Физический смысл мгновенной скорости
Быстрота изменения радиус-вектора или соответствующих его проекций во времени.
● Геометрический смысл мгновенной скорости
Вектор мгновенной скорости направлен по касательной к траектории в данной точке.
● Среднее ускорение |
ar |
|
|
|
|
|
|||
Вектор, равный отношению приращения вектора скорости |
|||||||||
точки |
|
к промежутку времени |
t , в течение которого это |
||||||
υ |
|||||||||
приращение произошло: |
|
|
υy , |
|
υz . |
||||
ar = |
υ |
|
ax = |
υx , |
ay = |
az = |
|||
|
t |
|
|
t |
|
t |
|
t |
|
● Мгновенное ускорение (полное ускорение) a
Вектор, равный пределу среднего ускорения при неограниченном уменьшении промежутка времени, в течение которого рассматривается движение точки, то есть первой производной вектора скорости по времени или второй производной радиус-вектора точки по времени:
(1.4) |
r |
= |
lim |
r |
= |
lim |
υ |
= |
dυ |
= |
d 2r |
|
|
|
|
|||||
a |
a |
|
t |
dt |
dt2 |
|
|
|
||||||||||||
|
|
|
t→0 |
|
|
t→0 |
|
|
|
|
|
2 |
|
|
||||||
|
|
= lim |
|
ax |
= lim |
|
|
υx |
= dυx |
= d |
x |
, |
||||||||
|
ax |
|
|
|
|
|||||||||||||||
|
|
|
t→0 |
|
t→0 |
t |
|
|
dt |
|
|
|
dt2 |
|
||||||
(1.4′) |
|
|
= lim |
|
ay |
= lim |
|
υy |
= |
dυy |
= |
d 2 y |
, |
|||||||
ay |
|
|
t |
|
|
dt |
|
dt |
2 |
|||||||||||
|
|
|
t→0 |
|
t→0 |
|
|
|
|
|
|
|
||||||||
|
|
|
|
az |
= lim |
|
|
υz |
|
= |
dυz |
= |
d 2z |
. |
|
|||||
|
az = lim |
|
|
t |
|
dt |
|
|
2 |
|
||||||||||
|
|
|
t→0 |
|
t→0 |
|
|
|
|
|
dt |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
●Физический смысл мгновенного ускорения
-23 -

Быстрота изменения вектора скорости во времени, представимая в виде быстроты изменения скорости по модулю (тангенциальное ускорение aτ ) и быстроты
изменения rвектора скорости по направлению (нормальное ускорение an ):
(1.5) ar = ddυt = ddυtτ + ddυtn = arτ + arn .
В выражении (1.5) вектор полного ускорения a сонаправлен с бесконечно малым приращением вектора
скорости |
|
, а не υ ! Аналогичное утверждение |
||||
dυ |
||||||
относится и к двум другим парам векторов arτ − |
|
и |
||||
dυτ |
||||||
r |
|
|
r |
|||
|
||||||
an − dυn . Вектор тангенциального ускорения |
aτ |
|||||
сонаправлен с вектором скорости υ , который и называют линейной скоростью.
●Геометрический смысл мгновенного ускорения
Тангенциальная составляющая вектора мгновенного ускорения направлена по касательной к траектории движения точки, а нормальная – перпендикулярна указанной касательной.
●Общий вид законов поступательного движения:
|
r |
|
r |
|
r t |
|
|
r t |
|
r t |
||
|
r |
(t) |
= r0 |
+ i ∫υx (t)dt + |
j ∫υy (t)dt + k ∫υz (t)dt, |
|||||||
|
|
|
|
|
|
|
t0 |
|
t0 |
|
t0 |
|
|
|
|
|
r |
|
r t |
|
r t |
|
r t |
||
(1.6) |
r |
|
+ |
+ |
+ |
|||||||
υ |
|
(t) |
=υ |
0 |
i |
∫ax (t)dt |
j ∫ay (t)dt |
k ∫az (t)dt, |
||||
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
t0 |
|
t0 |
|
t0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
|
|
r |
|
|
|
|
|
||
|
a(t) = f (t)n, |
|
|
|
|
|||||||
где n – единичный вектор, характеризующий направление ускорения в пространстве.
Частным случаем законов поступательного движения является равнопеременное движение материальной точки.
●Векторный способ задания равнопеременного движения материальной точки:
(1.7) rr(t) = rr |
+υr |
t + |
1 art2; υr(t) =υr |
+ art; ar = const. |
|
0 |
0 |
|
2 |
0 |
|
|
|
|
|
|
|
|
|
|
|
- 24 - |
|
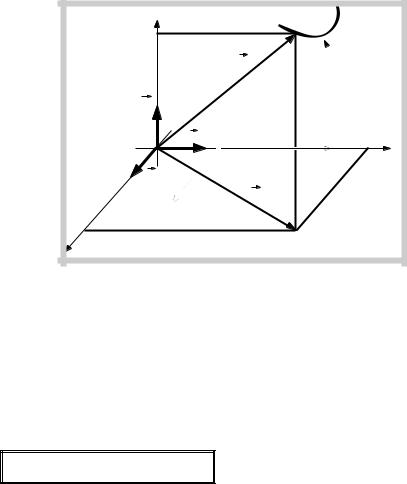
●Координатный способ задания равнопеременного движения материальной точки:
x(t)
(1.8) y(t)
z(t)
=x0 +υ0 xt + 12 axt2;
=y0 +υ0 yt + 12 ayt2;
=z0 +υ0zt + 12 azt2;
υx (t) =υ0 x + axt; |
ax = const, |
υy (t) =υ0 y + ayt; |
ay = const, |
υz (t) =υ0z + azt; |
az = const. |
Проекции радиус-вектора, скорости и ускорения имеют знак «+», если при проектировании того или иного вектора на
координатные |
оси |
направление |
его |
соответствующей |
|||
составляющей совпадает с направлением единичных ортов |
|||||||
ir, rj , kr |
декартовой системы координат |
и знак |
«–», если |
||||
процедура |
проектирования |
обнаруживает |
разные |
||||
направления |
|
|
|
|
|
|
|
составляющей |
|
Z |
|
|
|
|
|
рассматриваемого |
.z(t) |
|
|
|
траектория |
||
|
|
|
r(t) |
||||
вектора |
|
и |
|
|
|
||
|
|
|
|
материальной |
|||
единичных ортов. |
|
|
|
|
точки |
||
k |
|
|
|
|
|||
При решении |
задач |
0 |
|
j |
|
y(t) |
|
|
|
|
|
. Y |
|||
часто |
необходимо |
i |
|
|
|
|
|
использовать |
|
x(t). |
|
|
rxy (t) |
|
|
принцип |
|
|
|
|
|
||
независимости |
X |
|
|
|
|
||
движений. |
|
|
|
|
|
|
|
● Принцип независимости движений
Любое движение материальной точки (тела) может быть представлено в виде суперпозиции (наложения или векторной суммы) двух или более независимых движений, определяемых в одной системе отсчета.
***** Глава1. §3 *****
- 25 -
§4. Естественное задание прямолинейного и плоского движения материальной точки
● Прямолинейное движение
Движение, совершаемое материальной точкой вдоль одной прямой (например, вдоль оси ОХ декартовой системы координат).
● Перемещение |
X (t)= x(t) − x0 |
|
при |
равнопеременном |
||||
движение за промежуток времени от t=0 до t=T |
||||||||
|
X (t)= x(t) − x |
0 |
=υ |
0x |
t + |
1 a |
x |
t2; |
|
|
|
|
2 |
|
|||
(1.9) |
υx (t) =υ0x + axt; |
|
|
|
|
|||
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
a = const.
x
Знак величины Х указывает на направление перемещения: «+» – по оси ОХ, «–» – против оси ОХ.
● Длина пути L1 либо при равноускоренном, либо при
равнозамедленном движении
(1.10) L1 = X .
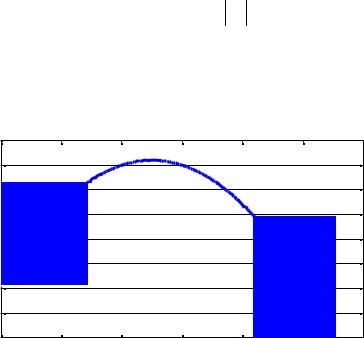
●Длина пути L(t) (график зависимости пути L от времени t) при равнопеременном характере движении:
|
|
a) υ0x > 0, |
ax < 0 |
|
|
|
X, m |
|
|
|
|
|
|
35 |
|
|
|
x(t)=11+10t-t 2 |
|
|
30 |
|
|
|
|
|
|
25 |
|
|
|
|
|
|
20 |
|
|
|
|
|
|
15 |
|
|
|
|
|
|
10 |
|
|
|
|
|
|
5 |
|
|
|
|
|
|
0 |
2 |
4 |
6 |
8 |
10 |
t,c |
- 26 -
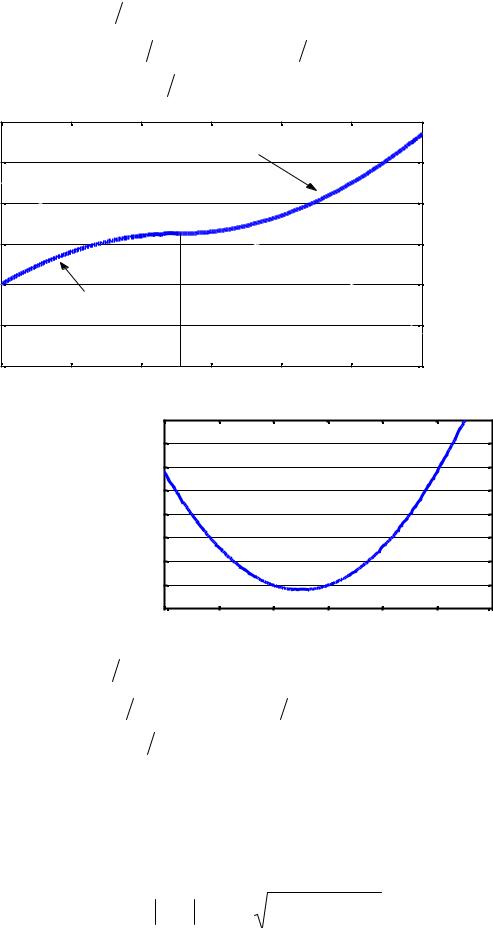
(1.11) |
|
|
|
2 |
|
|
|
0 ≤ t ≤ t0 , |
L(t)= υ0 xt + 1 2axt |
2 |
|
|
2 |
||||
|
|
|
|
|
|
t0 ≤ t, |
||
|
|
2(υ0 xt0 + 1 2axt0 )−υ0 xt −1 2axt |
|
|||||
|
|
|
t0 = −υ0 x |
ax . |
|
|
|
|
|
L, m |
|
|
|
|
|
|
|
|
|
|
|
L(t)=t 2 -10t+50 |
|
|
|
|
|
60 |
|
|
|
|
|
|
|
|
40 |
|
|
|
|
|
|
|
|
20 |
|
|
|
|
|
|
|
|
0 |
L(t)=10t-t 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
-20 |
|
|
|
|
|
|
|
|
|
|
t0 |
|
|
|
|
|
|
-40 |
2 |
4 |
6 |
8 |
10 |
t, c |
|
|
0 |
|||||||
|
|
|
|
X, m |
|
|
|
|
|
|
|
|
||
● Длина пути |
|
L(t) |
35 |
|
|
|
|
|
|
|
|
|||
(график |
|
|
|
30 |
|
|
|
|
|
|
|
|
||
зависимости пути L |
25 |
|
|
|
|
|
|
|
|
|||||
от |
времени |
t) |
при |
20 |
|
|
|
|
|
|
|
|
||
равнопеременном |
|
15 |
|
|
|
|
|
|
|
|
||||
характере |
|
|
|
10 |
|
|
|
|
2 |
|
|
|
||
движении: |
|
|
|
|
|
|
|
|
|
x(t)=t -10t+29 |
|
|
||
|
|
|
5 |
|
|
|
|
|
|
|
|
|||
b) υ0 x < 0, |
ax > 0 |
|
0 |
2 |
4 |
6 |
|
8 |
10 t, c |
|||||
(1.12) |
−υ |
0 x |
t −1 2a |
x |
t2 |
|
|
|
|
0 ≤ t ≤ t |
0 |
, |
||
L(t)= |
|
|
2 |
|
|
|
2 |
|
|
|
||||
|
|
|
|
|
|
|
|
|
t0 |
≤ t, |
|
|
||
|
|
2(υ0 xt0 + 1 2axt0 )+υ0 xt + 1 2axt |
|
|
|
|||||||||
|
|
|
t0 = −υ0 x |
|
ax . |
|
|
|
|
|
|
|
|
|
● Плоское движение
Движение, полностью описываемое на плоскости XOY декартовой системы координат.
● Длина пути s(t) за время движения от t0 до t
(1.13) |
t |
t |
s(t0 ,t) = ∫υr(t)dt = ∫ υx2 (t) +υ2y (t)dt. |
||
|
t0 |
t0 |
|
- 27 - |
|
● Траектория движения |
|
|
|
|
Зависимость y=y(x) |
и соответствующий график функции |
|||
(1.14) |
y = y(x). |
|||
|
|
|
|
|
|
***** |
Глава1. §4 ***** |
|
|
|
|
|
|
|
§5. Кинематика вращательного движения
Так как кинематика еще не закончилась, приходится вновь и вновь вводить новые определения.
● Вращательное движение тела
Движение, при котором одна прямая, связанная с телом, не перемещается, являясь неподвижной относительно системы отсчета, и называется осью вращения; траектории всех точек вращающегося тела представляют собой концентрические окружности, плоскости которых перпендикулярны оси вращения, а центры лежат на этой оси.
Очевидно, определения поступательного или вращательного движения неприменимы к движению материальной точки, с одной стороны. С другой стороны, материальная точка не может находиться в стороне от этих понятий или возвышаться над ними. Следовательно, логично заключить, что для точки одинаково справедливо применение понятий и терминов как поступательного, так и вращательного движений. Выбор терминологии определяется соображениями удобства описания условий конкретной задачи и оптимальности вычисления искомой физической величины.
Нетрудно заключить, что между кинематическими характеристиками поступательного и вращательного движений материальной точки существует вполне определенная связь. В дальнейшем такая кинематическая связь двух видов движений материальной точки будет приведена и использована при решении задач. К стати сказать, что других видов движений, кроме указанных, и не существует, разве что их комбинация.
-28 -
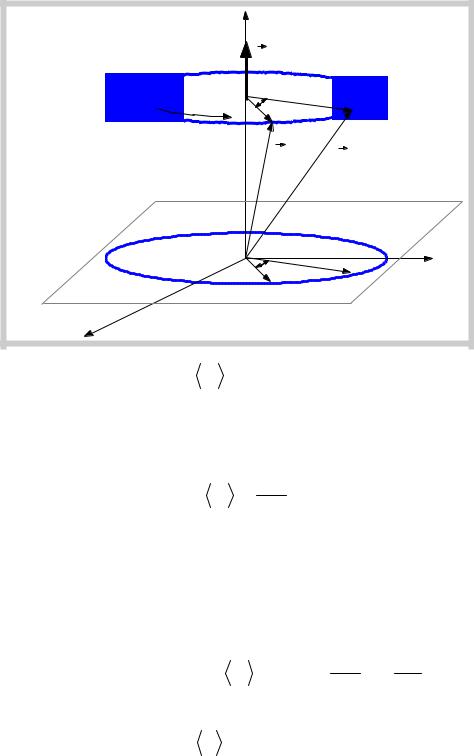
● Вектор элементарного поворота dϕ |
|
|||
Вектор, величина которого равна элементарному углу |
||||
поворота радиус-вектора материальной точки r (t) за |
||||
промежуток времени dt , а направление определяется по |
||||
правилу правого винта (буравчика), рукоятка которого |
||||
движется в том же направлении, что и точка (см. рис.). |
||||
|
|
Z |
|
|
|
|
.dϕ dϕ |
|
|
|
|
|
r ( t ) |
r ( t + dt ) |
|
|
|
|
|
|
|
. dϕ |
Y |
|
|
|
|
||
|
X |
|
|
|
● Средняя угловая скорость ωr |
|
|
||
Вектор, равный отношению вектора углового перемещения |
||||
ϕ |
ко времени |
t , в течение которого произошло это |
||
событие: |
|
ϕ . |
|
|
|
|
ω = |
|
|
● Мгновенная угловая скорость ω |
t |
|
||
|
|
|||
Вектор, равный пределу средней угловой скорости при |
||||
неограниченном уменьшении промежутка времени, в |
||||
течение которого произошел поворот: |
|
|||
(1.15) |
r |
r |
|
ϕ |
= |
dϕ |
. |
ω = lim |
ω = lim |
|
|
dt |
|||
|
t→0 |
t→0 |
|
t |
|
|
● Среднее угловое ускорение εr
- 29 -

Вектор, равный отношению изменения вектора угловой скорости ω ко времени t , за которое это изменение произошло:
εr = ωt .
● Мгновенное угловое ускорение ε
Вектор, равный пределу среднего углового ускорения при неограниченном уменьшении промежутка времени, в течение которого произошел поворот:
(1.16) |
r |
r |
= |
lim |
|
ωr |
= |
dω |
= |
d 2ϕ |
. |
ε = lim |
ε |
|
|
dt |
dt2 |
||||||
|
t→0 |
|
|
t→0 |
t |
|
|
|
|||
● Общий вид законов вращательного движения:
(1.17) |
t |
t |
ϕ(t) = ϕ0 + ∫ω(t)dt; |
ω(t) = ω0 + ∫ε(t)dt; ε(t) = f (t). |
|
|
t0 |
t0 |
Уравнения (1.17) в отличие от аналогичной системы (1.6) написаны в скалярном, а не векторном виде. Это не случайно, так как координатного способа представления закона вращательного движения не требуется (векторы угловой скорости ω и углового ускорения ε направлены
вдоль оси вращения, являясь аксиальными векторами).
Между векторными величинами поступательного и вращательного движений существует определенная связь.
●Закон равнопеременного вращательного движения:
(1.18) ϕ(t) = ±ϕ0 ±ω0t ± |
1 |
εt2; ω(t) = ±ω0 ± εt; ± ε = const. |
|
2 |
|
Выбор знака в формулах (М 1.16) определяется по правилу буравчика: знак плюс выбирается в том случае, когда направление поступательного движения острия буравчика синхронизировано с движением точки по окружности, которая при этом движется в том же направлении, что и рукоятка буравчика.
***** Глава1. §5 *****
- 30 -
