
Лекции №1
.pdf
скачкообразного возмущения на выходе получается мгновенный выходной импульс, теоретически имеющий бесконечно большую амплитуду, соответствующую бесконечно большой скорости изменения входной величины в момент подачи входного сигнала.
Выполнить идеальное дифференцирующее звено из пассивных элементов нельзя. Известным приближением к идеальному дифференцирующему звену является случай, когда в реальном звене выполняется условие p T << 1 . Это означает, что реальное звено приближается к идеальному,
если постоянная времени звена мала и звено работает на низких частотах или при медленно меняющихся процессах.
Уравнение звена в операторной форме Y ( p) = T p X ( p) дает возможность получить выражение для передаточной функции W ( p) = Y ( p) / X ( p) = p T . При действии на, входе звена единичной функции переходная функция представляет собой функцию Дирака, аналитическое выражение которой имеет вид h(t) = 0 при t>< 0 ; h(t) = ∞ при t = 0 . Это видно и из следующих соображений: единичная функция остается неизменной при всех значениях t>< 0 , так как при t < 0 x(t) = 0 , а при t > 0 x(t) = 1 . Это означает, что первая производная при этом равна нулю; в
момент, когда t = 0 , функция скачком меняется от 0 до 1, а первая производная, определяющая тангенс угла наклона касательной, становится равной бесконечности, так как угол наклона касательной равен π / 2 (рис. 24,б). Получение всплеска выходной координаты до значения, равного бесконечности, с помощью пассивных элементов невозможно и теоретически такой всплеск возможен лишь при наличии некоторого «резервуара» неограниченной мощности.
Так как передаточная функция в частотной форме W ( j ω ) = j ω T , то годограф
представляет собой прямую, совпадающую с осью положительных значений мнимых величин и простирающуюся от j 0 до j ∞ (рис. 24,в).
ЛАЧХ - бесконечная прямая с наклоном +20 дБ/дек., ЛФЧХ - прямая, параллельная оси lgω
с неизменной ординатой, равной π / 2 . Аналитическое выражение для ЛАЧХ: L(ω |
) = 20 lgω T , а |
для ЛФЧХ ϕ (ω ) = arctg(∞ ) = π / 2 . ЛАЧХ пересекается с осью частот там, где ω |
= 1/ T , так как |
ω T = 1, а lgω T = 0 . |
|
10.9. Реальное дифференцирующее звено со статизмом
Применяют, как правило, для цепей последовательной коррекции САУ для улучшения работы системы. Часто используют электрическую схему, которая обладает свойствами дифференцирующего звена, проявляющимися на некотором диапазоне частот (рис. 25,г).
Уравнение движения звена, связывающего входную и выходную координаты, имеет вид: y(t) + K T dy / dt = K [x(t) + T dx / dt].
Если на входе звена действует единичная функция, решением дифференциального уравнения |
|||||||
является переходная функция h(t) = K [1 − |
(1 −1/ K ) e−t k / T ]. Графически переходная функция |
||||||
имеет вид, показанный на рис. 25,а. |
|
|
|
|
|
||
Выражение |
для |
передаточной |
функции |
звена |
в |
операторной |
форме: |
W ( p) = K (1 + p T )/(1 + p K T ), в частотной форме W ( j ω ) = K |
(1 + j ω |
T )/(1 + j ω |
K T ), где |
||||
K < 1. При изменении |
частоты от 0 до ∞ |
W ( j ω ) |
меняется |
от 1 |
до K . Не |
подставляя |
|
промежуточных значений, можно сказать следующее: так как звено обладает дифференцирующими свойствами, то его годограф должен находиться в первом квадранте комплексной плоскости. И действительно, годограф представляет собой полуокружность с
центром в точке |
A с координатами (1+ K ) / 2; |
j 0 |
(рис. 25,б). |
|
|
|
|
Построение ЛАЧХ и ЛФЧХ (рис. 25,б). Известно, что модуль отношения векторов равен отношению модулей векторов. Аналитическое выражение для ЛАЧХ:
L (ω ) = 20lg |
|
K (1+ jω T ) / (1+ ωj |
K T ) |
|
= 20lg (K |
|
1ω+ j |
T |
|
/ |
|
1ω+ j K T |
|
) = 20lg K + |
||
|
|
|
|
|
|
|||||||||||
+ 20lg 1+ ω 2 T 2 − 20 lg 1 + ω 2 K 2 T 2 = L (ω )+ L |
2 |
(ω )+ L (ω ). |
||||||||||||||
Графически ЛАЧХ L1 (ω ) |
1 |
|
|
3 |
|
|
|
|
|
|
||||||
представляет |
собой |
прямую, параллельную оси абсцисс и |
||||||||||||||
проходящую ниже нулевого уровня, так как K < 1.
31
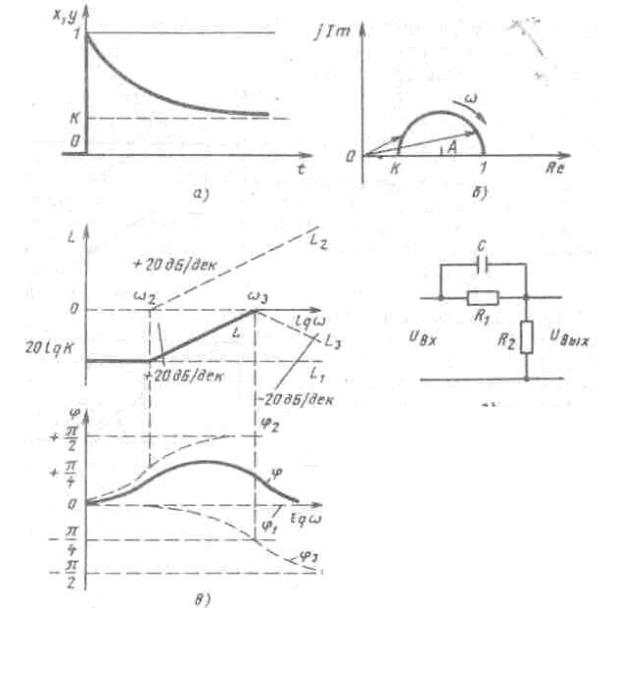
Рис. 25. Характеристики реального дифференцирующего звена со статизмом: а - переходная; б - амплитудяо-фазовая: в - ЛАЧХ и ЛФЧХ; г - электрическая модель звена
|
Частота |
сопряжения |
для |
L2 (ω ) |
(ω 2 = 1/T ) |
ниже, |
чем |
для |
характеристики |
L3 (ω ) |
|||||||||
(ω 3 = 1/ KT ) , так как K < 1. Очевидно и то, что ордината L2 (ω ) |
на частоте ω 3 равна − 20 lg K > 0 . |
||||||||||||||||||
В |
самом |
деле, |
на |
частотах |
ω > ω 2 |
L2 (ω ) ≈ 20lgω( T ) . |
|
При |
ω = ω 3 |
= 1/ KT , |
|||||||||
L3 (ω |
) ≈ 20 lg (1/ KT ) |
T= 20 lg (1/ K )= 20 lg1− 20lg K= − 20lg K . |
|
Поэтому |
результирующая |
||||||||||||||
характеристика L(ω ) на частотах ω ≥ ω |
3 , проходит на нулевом уровне или, иными словами, |
||||||||||||||||||
совпадает с осью lgω . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Аналитическое |
|
|
|
выражение |
|
|
|
|
|
для |
|
|
|
|
ЛФЧХ: |
|||
ϕ (ω |
) = arg[K ] + arg[1+ jω |
T ] − arg[1+ ωj |
K T ] = ϕ 1 +ϕ 2 |
ϕ+ |
3 , |
где |
ϕ 1 |
= 0 , |
так |
как |
вектор |
||||||||
содержит только действительную часть; ϕ 2 = arg[1+ jω |
T |
] = arctg(ω |
T ), которая в области низких |
||||||||||||||||
частот, когда ω стремится к 0, близка к +0, на частоте сопряжения ω |
= 1/ T равна + π / 4 , а при |
||||||||||||||||||
ω → |
∞ стремится |
к + π |
/ 2 ; |
ϕ 3 |
= −arg[1 + j ω |
K T ] = −arctg(ω |
K T ) |
меняется |
в |
области |
|||||||||
отрицательных значений и при ω |
→ |
0 близко к ϕ 3 |
−0 . |
|
|
|
|
|
|
|
|
|
|
||||||
Колебательное звено (апериодическое звено второго порядка). Рассмотрим механическую систему, пример которой приведён на рис. 26,а. Жидкость вытесняется через зазор между
32
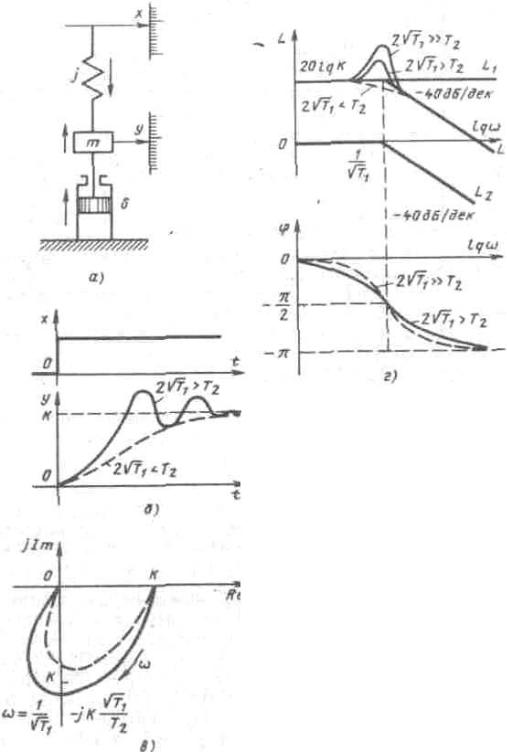
поршнем и стенкой. Создается трение, характеризуемое коэффициентом δ . Если приложим входную величину x , то пружина сначала сожмётся, затем начнётся перемещение массы, которая, двигаясь по инерции, пройдет положение равновесия и растянет пружину. Составляем уравнение.
n
Сумма всех сил, действующих на систему ∑ Pi = 0 . При приложении x инерционные силы и
|
|
|
|
i=1 |
|
|
|
|
PУПР − РИН − РВ.С. = 0 ; |
||
силы сопротивления вязкой среды будут действовать в обратную сторону: |
|||||||||||
РУПР = j (x − y) ; |
PИН = m y ; |
PB.C. = δ y ; где y - скорость перемещения. |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
n |
|
|
Подставляя |
значения |
РУПР , |
PИН , |
PB.C. |
в |
уравнение |
|
∑ Pi = 0 , |
получим |
||
− j y − m y − δ |
y = − j x , |
|
|
|
|
|
|
i=1 |
|
j , |
|
разделим |
обе |
части |
этого |
уравнения |
на |
||||||
тогда T y + T |
y + y = x , где T = m / |
j , с2; T |
= δ / |
j , с. |
|
|
|
|
|
||
1 |
2 |
|
1 |
2 |
|
|
|
|
|
|
|
Рис. 26. Характеристики колебательного звена: а – механическая модель звена; б
– переходная; в – амплитуднофазовая; г – ЛАЧХ и ЛФЧХ
33
Уравнение |
движения |
колебательного |
звена: |
T d 2 y / dt2 |
+ T |
|
dy / dt + y(t) = K x(t) . |
|
|
|
|
|
1 |
2 |
|
|
|
Перейдем от оригиналов к изображениям: T p2 |
Y ( p) + T p Y ( p) + Y |
( p) = K X ( p) . |
|
|||||
|
|
1 |
|
2 |
|
|
|
|
Передаточная |
функция |
W (p) = Y ( p) / X ( p) = K /(T p2 + T p +1). |
При 2 T |
> T звено |
||||
|
|
|
1 |
2 |
|
|
1 |
2 |
обладает колебательными свойствами. Если это условие не соблюдается, то колебательное звено вырождается в апериодическое. Если X ( p) = 1/ p (единичная функция), то переходная функция
имеет вид h(t) = K 1+ e−t /T |
cosω |
|
t + |
|
1 |
|
sinω |
|
t |
|
, где T = 2 T / T ; ω |
|
= |
4 T − T 2 |
/ 2 T . |
||||||
0 |
|
|
|
0 |
|
0 |
|||||||||||||||
|
|
|
|
|
|
ω 0 T |
|
|
|
1 |
2 |
|
1 |
2 |
1 |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
W ( j ω ) = K /(1− ω 2 T + j ω |
T ). Амплитудно-фазовая |
характеристика |
колебательного |
||||||||||||||||||
|
|
1 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
звена имеет вид, показанный на рис. 26,в. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Для построения ЛАЧХ и ЛФЧХ (рис. 26,г) находят выражения для модуля и фазы вектора |
|||||||||||||||||||||
W ( j ω ) в следующем |
виде: |
для |
|
модуля |
A(ω ) = K / |
(1 − ω 2 T )2 + ω |
2 T 2 |
; для фазового угла |
|||||||||||||
ϕ ω( ) = arctg ω− |
T2 / (1ω − |
|
T1 ) . |
|
|
|
|
|
|
|
|
|
|
1 |
|
2 |
|
A(ω |
), |
|
|
2 |
|
|
|
Логарифмируя |
выражение |
|
найдем |
||||||||||||||
L(ω ) = 20 lg K − 20 lg (1 − ω |
2 T )2 + ω 2 T 2 . |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
1 |
|
L(ω |
2 |
|
ϕ (ω |
|
), |
|
|
|
|
|
|
|
|
|
|
Используя |
выражение |
для |
|
) |
и |
|
строят |
логарифмические |
характеристики |
||||||||||||
колебательного звена с учетом допущений, которые имели место при нахождении асимптотической ЛАЧХ инерционного звена. Для построения асимптотической ЛАЧХ
колебательного звена следует найти значение ω = 1/ T1 , провести прямую, параллельную оси частот и отстоящую от нее на величину 20lg K , до точки с частотой ω = 1/ T и из этой точки
провести прямую с наклоном (-40дБ/дек). Следует учитывать, что построение асимптотической ЛАЧХ колебательного звена связано с наличием существенной погрешности, зависящей от
коэффициента затухания χ = T2 / 2 T1 при χ |
= 0.5 ошибка минимальна. |
10.10. Запаздывающее звено |
|
Для любого устройства, служащего |
для передачи или преобразования информации, |
справедливо то, что выходная величина проявляется с некоторым запаздыванием на время τ относительно момента поступления информации на вход устройства. В ряде случаев это запаздывание настолько мало, что им пренебрегают, полагая τ = 0 , и считают, что практически информация на входе и выходе возникает в один и тот же момент времени. Однако есть и такие устройства, где этот временной сдвиг играет существенную роль. Если устройство не поглощает энергию, то x(t) и y(t) совпадают по виду функциональных зависимостей. Звено определяется
как запаздывающее, если оно описывается уравнением y(t) = x(t −τ ) , τ - время запаздывания.
Примерами запаздывающего звена могут быть длинная линия без потерь, длинный трубопровод, некоторые тепловые объекты (печи, нагреватели). Для идеального запаздывающего
звена передаточная функция имеет вид W (p) = e− p τ и W ( j ω ) = e− j ω τ . Годограф - окружность с
радиусом, равным 1, |
так как |
||||||
e− j ω τ = cosω |
τ |
− j sinω |
τ |
, |
а |
||
A(ω |
) = |
cos2 ω |
τ + sin 2 ω |
τ |
= 1 . |
||
|
Каждой |
|
точке годографа |
||||
соответствует |
бесконечное |
||||||
множество |
значений |
частот. |
|||||
Скользя своим концом по этой |
|||||||
окружности, |
|
вектор |
W ( j ω |
) |
|||
описывает по часовой стрелке |
|
||||||
при |
|
росте |
|
частоты |
|
всё |
|
возрастающий |
угол. |
При |
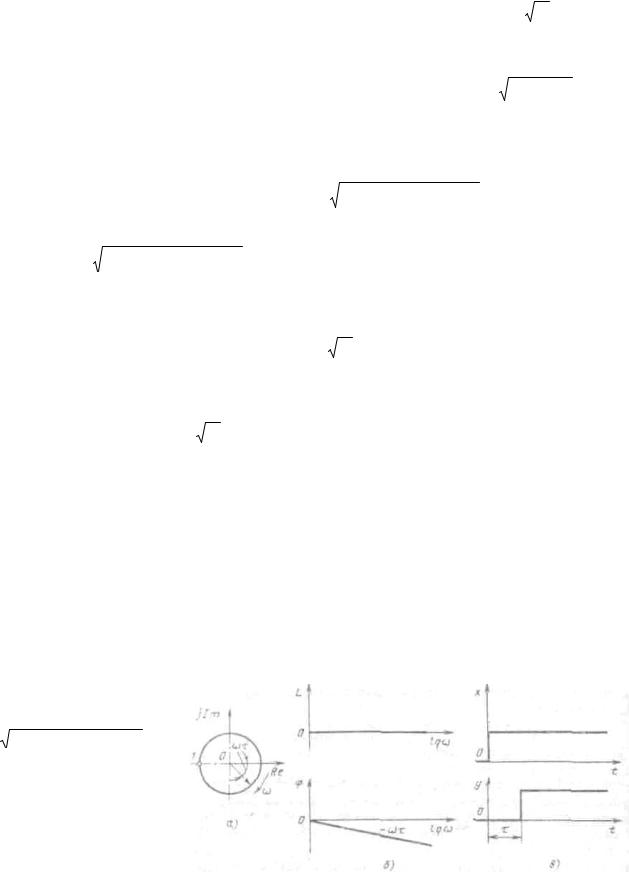
Рис. 27. Характеристики запаздывающего звена: а - |
||||
частотах, равных 0, 2 π |
/τ , |
амплитудно-фазовая; б - ЛАЧХ и ЛФЧХ; в - |
|||||
4 π |
/τ |
, значение W ( j ω ) = 1. |
переходная |
||||
34
ЛАЧХ запаздывающего звена совпадает с ЛАЧХ безынерционного звена с передаточным
коэффициентом |
K = 1. |
Аналитическое |
выражение |
ЛФЧХ |
ϕ (ω ) = arctg(− sinω |
τ / cosω τ ) = arctg(− tgω |
τ ) = −ω τ . Из |
фазочастотной характеристики сле- |
|
дует, что запаздывающее звено дает равномерное пропускание всех частот при сдвиге фаз, пропорциональном запаздыванию τ .
35

11. УСТОЙЧИВОСТЬ САУ
11.1.Математический признак устойчивости (критерий Ляпунова)
САУ, как любая динамическая система, характеризуется переходным процессом, возникающим в ней при нарушении её равновесия под воздействием сигнала управления, настройки или помех.
В переходном процессе различают две составляющие:
- свободные движения системы, определяемые начальными условиями и yB (t) - вынужденные движения, определяемые возмущающим воздействием и свойствами системы, т. е. y (t ) = yC (t) + yB (t ) .Чтобы САУ
могла правильно реагировать на сигнал управления, настройки или изменения нагрузки, в переходном процессе свободная составляющая с течением времени
должна стремиться к нулю, т. е. lim yC (t) → 0 , так как характер свободного движения
t→ ∞
системы определяет её устойчивость.
Для определения устойчивости САУ исследуют однородное дифференциальное уравнение описывающее свободные движения САУ. Такое уравнение линейной САУ, разрешенное относительно исследуемой величины, можно записать так:
C |
d n y |
|
|
d n−1 y |
|
|
dy |
|
y = 0 , |
|
C + C |
C |
+ ... + C |
C + C |
|||||||
dtn−1 |
||||||||||
0 |
dtn |
1 |
|
n−1 |
|
dt |
n |
C |
||
где C0 , C1 , …, Cn - постоянные коэффициенты, определяемые параметрами САУ. В операторной форме это уравнение имеет вид (C0 pn + C1 pn−1 + ... + Cn ) Y ( p) = 0 .
Отсюда характеристическое уравнение имеет вид
C0 pn + C1 pn−1 + ... + Cn = 0 .
Решение дифференциального уравнения при всех вещественных корнях имеет
вид
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
yC (t) = ∑ Ai eλ i t , |
|
|
||||
|
|
|
|
|
|
i=1 |
|
|
|
|
где Ai - постоянные интегрирования, определяемые |
параметрами системы и |
|||||||||
начальными условиями (всегда больше 0). |
|
|
|
|
||||||
Для системы, изображённой на рис. 28., |
|
|
|
|
||||||
|
|
W |
( p) = K K |
2 |
/ (1+ p T ) (1+ p T ) ; |
|||||
|
|
П |
|
1 |
|
1 |
|
2 |
|
|
|
|
W ( p) = Y ( p) / X |
( p) = W |
( p)/ 1+W ( p) |
||||||
или |
|
С |
|
|
|
П |
|
|
П |
|
|
|
|
( p) Y ( p) = W |
|
( p) X ( p) , |
|
||||
|
|
1+W |
|
|
||||||
|
|
|
П |
|
|
П |
|
|
|
|
где 1+W |
( p) - полином n -го порядка; W ( p) |
- полином m -го порядка, как правило, |
||||||||
|
П |
|
|
|
|
П |
|
|
|
|
n > m .
36

Подставляя вместо WP (p) выражение, определённое через параметры звеньев, получим
|
+ |
K1 |
K2 |
|
|
Y (p) = |
|
K1 |
K2 |
|
X (p). |
|
1 |
|
|
|
|
|
|
|
|||||
(1 + p T ) (1+ p T |
) |
(1 |
+ p T ) (1 |
+ p T |
) |
|||||||
|
1 |
2 |
|
|
|
|
1 |
|
2 |
|
|
|
|
|
Приводя |
обе |
части |
|
к |
|
общему |
знаменателю, |
получим |
выражение |
||||||||||||
[T T p2 |
+ (T + T ) p + 1+ K |
1 |
K |
2 |
] Y (p) = K |
1 |
K |
2 |
X (p) |
и уравнение, в котором правая и |
|||||||||||||
1 |
2 |
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
левая части являются полиномами от |
p |
|
(левая часть - полином второй степени, |
||||||||||||||||||||
правая |
- нулевой). Переходя |
от |
|
изображений к оригиналам, |
будем иметь |
||||||||||||||||||
T T |
2 |
d 2 y / dt 2 |
+ (T + T ) dy / dt + (1+ K |
1 |
K |
2 |
) y(t) = K |
1 |
K |
2 |
x(t), где |
левая часть - уравнение |
|||||||||||
1 |
|
|
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
собственных движений, а правая - уравнение вынужденных движений. Чтобы понять, система расходящаяся или сходящаяся, необходимо решить уравнение
только |
|
собственных |
движений |
|
|
|
T T |
|
d 2 y / dt 2 |
+ (T + T ) dy / dt + (1+ K |
1 |
K |
2 |
) y(t) = 0 , |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
2 |
|
|
|
|
|
|
1 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
решением которого будет сумма частных решений |
|
yC (t) = ∑ Ai |
|
eλ i t , |
где |
|
λ i |
|
корни |
|||||||||||||||||||||||||||||||||||||||
характеристического |
уравнения |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= 0 , |
|
|
где |
i=1 |
|
= T T ; |
|
C = T + T ; |
||||||||||||||||||||||||
|
C |
0 |
λ 2 |
+ C λ |
+ C |
2 |
|
|
|
C |
0 |
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
|
|
|
1 |
|
1 |
|
2 |
||||
C |
2 |
= 1 + K |
1 |
K |
2 |
. |
Его корни |
λ |
1,2 |
= −C / 2 C |
0 |
± |
C 2 |
− 4 C |
0 |
C |
2 |
/ 2 C |
0 |
. Если C 2 |
|
< 4 C |
0 |
C |
2 |
то |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|||||||||||
λ .1,2 |
= −C1 / 2 C0 |
± j C12 − 4 C0 C2 / 2 C0 , |
|
|
|
т.е. |
λ |
может |
|
в общем |
|
случае |
|
оказаться |
||||||||||||||||||||||||||||||||||
комплексным числом. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
Комплексные корни характеристического уравнения всегда бывают попарно |
|||||||||||||||||||||||||||||||||||||||||||||
сопряженными: λ /1 = α |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
||||||||
+ j β |
|
и |
λ / 2 |
|
= α |
|
− j β . |
Тогда |
уравнение |
yC (t) = ∑ Ai |
eλ i t |
в |
||||||||||||||||||||||||||||||||||||
соответствии с формулой Эйлера e+ jβ i t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i=1 |
|
|
|
|
|
|||||||||||||||||||
|
= cos β i t ± j sin β i |
t может быть представлено |
||||||||||||||||||||||||||||||||||||||||||||||
в следующем виде: |
|
j |
i ) t + A e( |
|
|
|
|
|
j ) |
|
= A* eα i t |
sin (β |
|
t +ϕ |
|
) , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
A e( i |
|
i |
− jβ |
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
α |
+ β |
|
|
|
|
|
α |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
i |
|
|
|
i+1 |
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где |
A* - начальная амплитуда; |
ϕ |
- начальная фаза. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Если α > 0 , то с увеличением t |
растет амплитуда. Если α |
< 0 , то с увеличением |
|||||||||||||||||||||||||||||||||||||||||||
t амплитуда стремится к нулю. Если α |
|
= 0 , то имеем чисто гармонический процесс. |
||||||||||||||||||||||||||||||||||||||||||||||
Поэтому вид кривой уравнения |
yC (t) |
|
|
определяется видом корней, которые могут |
||||||||||||||||||||||||||||||||||||||||||||
быть комплексно-сопряженные, чисто вещественные, чисто мнимые, нулевые, кратные.
Проанализируем |
кривую |
yC (t) |
при |
возможных |
|
видах |
корней |
|
|
|
|
S |
|
m |
|
k |
|
характеристического |
уравнения: |
yC (t) = ∑ Ai |
e±α i t e± j β i t + ∑ Ai |
e±α i t + ∑ Ai e± j β i t + |
||||
|
|
|
i=1 |
|
i=S +1 |
|
i=m+1 |
|
l |
|
|
|
|
|
|
|
|
+ ∑ Ai e0t + (Aq1 + Aq2 + ... + Aqγ ) e±α q t e± j β q t . Каждая |
составляющая |
- |
некоторая |
кривая |
||||
j=k +1 |
|
|
|
|
|
|
|
|
e±α i t , параметры которой изменяются от -1 до +1; кривая A e±α i t |
- показывает, как во |
|||||||
|
|
|
|
|
i |
|
|
|
времени изменяется амплитуда (рис. 29). Для оценки устойчивости надо определить
lim yC (t). |
Возможны, |
случаи: 1) |
если |
все |
α i |
< 0 , то |
lim yC (t) = 0 и, |
следовательно, |
t→ ∞ |
|
|
|
|
|
|
t→ ∞ |
|
система асимптотически устойчивая; |
2) если все α i < 0 , но среди корней имеются |
|||||||
нулевые |
или чисто |
мнимые |
корни, |
то |
lim yC (t) |
стремится |
к некоторому |
|
|
|
|
|
|
|
t→ ∞ |
|
|
|
|
|
|
|
|
|
|
37 |
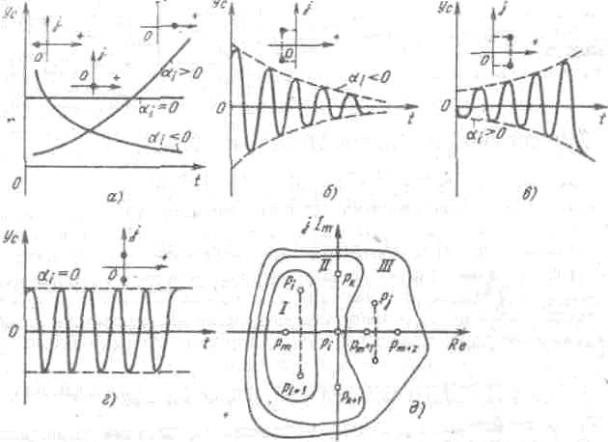
Рис. 29. Кривые, характеризующие переходные процессы для различных пар корней: а - корни вещественные: б - корни комплексно-сопряженные с отрицательной вещественной частью; в - корни комплексносопряженные с положительной вещественной частью; г - корни мнимые; д - расположение корней характеристического уравнения; I - устойчивая САУ; II - консервативная САУ; III - неустойчивая САУ
установившемуся |
процессу, определяемому нулевыми или |
мнимыми |
корнями |
(консервативная |
система); 3) если хотя бы одно значение |
α i > 0 , то |
lim yC (t) |
|
|
|
t→ ∞ |
стремится к бесконечности, т. е. система неустойчивая.
Замечание: особые трудности в обеспечении устойчивости возникают в системах с кратными корнями. Если кратный корень нулевой или чисто мнимый, система оказывается неустойчивой.
Вывод: необходимое и достаточное условие устойчивости линейных систем: среди корней характеристического уравнения отсутствуют нулевые и чисто мнимые корни; вещественные части всех корней характеристического уравнения
отрицательные. |
|
|
|
|
|
|
|
Пример. |
|
|
|
|
|
|
|
а) Пусть, мы имеем дифференциальное уравнение звена 0.1 |
d 2 y |
+ 2 dy + y = 2 x , |
|||||
|
|
||||||
|
|
2 |
dt 2 |
|
dt |
||
|
|
|
|
|
|
||
передаточная функция в операторной форме W (p) = |
|
|
, |
следовательно |
|||
0.1 p2 + 2 p + 1 |
|||||||
характеристическое |
уравнение |
0.1 p2 + 2 p + 1 = 0 ; |
|
дескриминант |
|||
|
|
|
|
|
|
|
38 |

D = b2 − 4 |
a c = 4 − 4 0.1 = 3.6 ; |
корни p1, 2 = − 2 ± |
3.6 = −19.5 и − 0.51. |
Оба корня имеют |
||||
|
|
|
2 0.1 |
|
|
|
|
|
отрицательную вещественную часть – система устойчива. |
|
|
|
|
||||
б) |
для |
случаев |
отрицательного |
дискриминанта, |
например |
для |
||
характеристического |
уравнения |
2 p2 + 2 p + 8 = 0 , |
дискриминант |
|||||
D = b2 − 4 |
a c = 4 − 4 2 8 = −60 , корни равны p |
= −2 ± −60 = −2 ± j |
−60 = −0.5± j |
60 |
. |
|||
|
||||||||
|
|
|
1, 2 |
4 8 |
4 8 |
|
4 8 |
|
|
|
|
|
|
||||
11.2.Другие критерии оценки устойчивости линейных САУ
Прямой метод анализа устойчивости систем связан с необходимостью определения корней (вычисление корней просто лишь для характеристического уравнения первой и второй степени). Существуют общие выражения для корней уравнений третьей и четвертой степеней, но эти выражения громоздки и практически мало пригодны. Что же касается уравнений более высоких степеней, то для них вообще невозможно написать общие выражения для корней через коэффициенты характеристического уравнения. Поэтому в инженерной практике применяют правила, которые позволяют определять устойчивость системы без вычисления корней. Эти правила называют критериями устойчивости. С помощью критериев устойчивости можно также выяснить, как влияют на устойчивость те или иные параметры и структурные изменения в системе.
Различают две группы критериев устойчивости: алгебраические (Рауса и Гурвица), основанные на анализе коэффициентов характеристического уравнения, и частотные (Михайлова, Найквиста), основанные на анализе частотных характеристик.
Замечание: частотные критерии позволяют оценивать устойчивость системы, даже если имеются в наличии только экспериментальные частотные характеристики.
1.Критерий Гурвица
Этот критерий позволяет, не решая уравнения, сказать, где на комплексной плоскости расположены его корни. Из коэффициентов характеристического уравнения C0 λ .n + C1 λ .n−1 + ... + Cn−1 λ + Cn = 0 n -го порядка строится сначала главный
определитель Гурвица по следующему правилу: по главной диагонали определителя слева направо выписываются все коэффициенты характеристического уравнения от C1 до Cn в порядке возрастания индексов. Столбцы вверх от главной диагонали
дополняются коэффициентами с последовательно возрастающими индексами, а столбцы вниз - коэффициентами с последовательно убывающими индексами. На место коэффициентов с индексами больше n (где n - порядок характеристического уравнения) и меньше нуля проставляют нули:
C1 C3 C5 C7 …0
C0 C2 C4 C6 …0
∆ n = 0 C1 C3 C5 …0 .
………………0
………………Cn
Выделяя в главном определителе Гурвица диагональные миноры, получаем определитель Гурвица низшего порядка
39

∆ |
|
= |
|
|
|
, ∆ |
|
= |
|
C1 C3 |
|
, ∆ |
|
|
C1 C3 C5 |
, … |
||||||
|
|
|
|
|
|
|
|
|||||||||||||||
1 |
|
C |
|
2 |
|
|
3 |
= |
C |
0 |
C |
2 |
C |
4 |
||||||||
|
|
|||||||||||||||||||||
|
|
|
1 |
|
|
|
|
C0 |
C2 |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
C1 C3 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Номер определителя Гурвица зависит от номера коэффициента по диагонали, до которого составляют данный определитель.
Определение: чтобы САУ была устойчива; необходимо и достаточно, чтобы определитель Гурвица и его диагональные миноры имели знаки, одинаковые со знаком коэффициента C0 характеристического уравнения, т. е. были
положительными, так как всегда C0 можно выбрать положительным.
Таким образом, при C0 > 0 для устойчивости системы необходимо и достаточно выполнение следующих условий:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
> 0 , ∆ |
|
|
|
|
C1 C3 |
|
> 0 , ∆ |
|
|
C1 C3 C5 |
> 0 , … |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
∆ |
1 |
= |
|
C |
|
2 |
|
= |
|
3 |
= |
C |
0 |
C |
2 |
C |
4 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
C0 C2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
C1 C3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
1. Система первого порядка. Характеристическое уравнение первого порядка C0 λ |
+ C1 |
= 0 . |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
Если |
|
C0 > 0 , |
C1 > 0 , то |
|
λ |
|
в левой части комплексной плоскости, |
|
следовательно, |
∆ |
= |
|
C1 |
|
> 0 , |
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
C1 |
> 0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
λ .2 |
+ C λ + C |
|
|
|
|
|
|
|
|
||||
|
|
|
2. Система второго порядка. Характеристическое уравнение |
C |
0 |
2 |
= 0 . Корни |
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
||
характеристического |
|
уравнения: |
λ |
1/ 2 |
= −C / 2 C ± |
C2 − 4 C C / 2 C . |
Возможны |
варианты, |
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
0 |
|
|
|
|
|
1 |
|
|
0 |
|
2 |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|||
если оба корня вещественные: а) |
C |
2 |
> 4 C |
0 |
C |
2 |
- корни только вещественные, |
если |
C |
0 |
> 0 и |
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
C > |
0 , то λ |
.1 |
< 0 , λ |
.2 |
<< 0 ; б) |
|
|
C 2 |
< 4 C |
0 |
C |
2 |
|
- |
корни комплексно-сопряженные, |
следовательно, |
||||||||||||||||||||||||||||||||||||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
можно записать λ 1/ 2 |
=α |
|
± j β |
|
. Так как α |
= −C1 / 2 C0 < 0 , |
если C0 > 0 и C1 > 0 . Определитель |
|||||||||||||||||||||||||||||||||||||||||||||||||||
∆ |
2 |
= |
|
C1 C3 |
|
> 0 , если C |
0 |
> 0 , ∆ |
2 |
= C C |
2 |
> 0 , |
∆ |
1 |
= |
|
C |
|
|
> 0 , при C > 0 . |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
C0 C2 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Вывод: для устойчивой системы второго порядка все коэффициенты характеристического уравнения должны иметь один и тот же знак.
3. Система третьего порядка. Характеристическое уравнение C0 λ .3 + C1 λ .2 + C2 λ + C3 = 0 . Главный определитель
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C1 C3 0 |
|
> 0 , если C0 > 0 . |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∆ 3 = |
C0 C2 0 |
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
C1 C3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Так как младший диагональный минор |
∆ 1 = |
|
C1 |
|
, то по Гурвицу |
C1 > 0 . Минор второго |
|||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||
порядка ∆ |
2 |
= |
|
C1 C3 |
|
= C C |
2 |
− C |
0 |
C |
3 |
> 0 , если система устойчива. |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
C0 |
C2 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Воспользуемся правилом Саррюса и определим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
C1 C3 |
0 |
|
= C C |
|
C |
|
|
|
C 2 = C |
|
|
(C C |
|
|
|
|
C |
) |
|
|
∆ |
|
. |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
∆ |
3 |
= |
C |
0 |
C |
2 |
0 |
2 |
3 |
− C |
0 |
0 |
2 |
− C |
0 |
= C |
3 |
2 |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
3 |
|
|
1 |
|
|
3 |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
0 |
|
C1 C3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
По Гурвицу для устойчивой системы ∆ 3 |
> 0 , но так как ∆ 2 |
> 0 , то C3 |
> 0 . Из минора ∆ 2 |
||||||||||||||||||||||||||||||||||||||
следует, что C2 > C0 C3 / C1 , а так как C0 |
|
> 0 , C3 > 0 |
|
и C1 > 0 , то C2 |
> 0 . |
|
|
|
|
|
|||||||||||||||||||||||||||||||
Таким образом, система третьего порядка устойчива, если: а) C0 > 0 , C1 |
> 0 , C2 > 0 , C3 > 0 ; |
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
40 |
