
- •Учреждение образования Белорусский государственный университет информатики и радиоэлектроники
- •Общие сведения Сведения об эумк
- •Методические рекомендации по изучению дисциплины
- •Рабочая учебная программа
- •Учреждение образования
- •«Белорусский государственный университет
- •Информатики и радиоэлектроники»
- •Пояснительная записка
- •Содержание дисциплины
- •2. Перечень тем практических занятий, их содержание и объем в часах
- •3. Литература
- •3.2 Дополнительная
- •4. Контрольные работы, их характеристика
- •5. Учебно-методическая карта дисциплины
- •Теоретический раздел Лекция 1
- •1.1 Введение
- •1.2 Основные понятия
- •1.3 Аксиомы теории вероятностей
- •1.4 Непосредственный подсчет вероятностей
- •1.5 Основные комбинаторные формулы
- •Лекция 2
- •2.1 Геометрическое определение вероятностей
- •2.2 Теоремы сложения вероятностей
- •2.3 Условная вероятность
- •2.4 Зависимые и независимые события
- •2.5 Теоремы умножения вероятностей
- •2.6 Вероятность безотказной работы сети
- •Лекция 3
- •3.1 Формула полной вероятности
- •3.2 Формула Байеса
- •3.3 Теорема о повторении опытов
- •Формула Пуассона
- •Формулы Муавра-Лапласа
- •Лекция 4
- •4.1 Случайные величины. Закон распределения вероятностей
- •4.2 Функция распределения
- •4.3 Ряд распределения
- •4.4 Плотность распределения
- •Лекция 5
- •5.1 Числовые характеристики случайной величины
- •5.1.1 Математическое ожидание
- •5.1.2 Начальные моменты
- •5.1.3 Центральные моменты
- •5.1.4 Дисперсия
- •5.1.5 Среднее квадратическое отклонение
- •5.1.6 Мода
- •5.1.7 Медиана
- •6.2 Типовые законы распределения непрерывных случайных величин
- •6.2.1 Равномерное распределение
- •6.2.2 Экспоненциальное распределение
- •6.2.3 Нормальное распределение
- •Лекция 7
- •7.1. Закон распределения функции случайного аргумента
- •7.1.1 Монотонно возрастающая функция
- •7.1.2 Монотонно убывающая функция
- •7.1.3 Немонотонная функция
- •7.2 Числовые характеристики функции случайного аргумента
- •7.2.1 Характеристическая функция случайной величины
- •Лекция 8
- •8.1 Двухмерные случайные величины. Двухмерный закон распределения
- •8.1.1 Двухмерная функция распределения
- •8.1.2 Матрица распределения
- •8.1.3 Двухмерная плотность распределения
- •8.2 Зависимые и независимые случайные величины
- •8.3 Условные законы распределения
- •Лекция 9
- •9.1 Числовые характеристики двухмерных величин
- •9.1.1 Смешанные начальные моменты
- •9.1.2 Смешанные центральные моменты
- •9.1.3 Корреляционный момент
- •9.1.4 Коэффициент корреляции
- •9.2Условные числовые характеристики
- •9.2.1 Pегрессия
- •Лекция 10
- •10.1 Нормальный закон распределения на плоскости
- •10.2 Закон распределения функции двух случайных величин
- •10.3 Многомерные случайные величины
- •10.3.1 Функция распределения
- •10.3.2 Плотность распределения
- •10.3.3 Числовые характеристики
- •11.2.2 Теорема о дисперсии суммы
- •11.3 Числовые характеристики произведения случайных величин
- •11.3.1 Теорема о математическом ожидании произведения
- •11.3.2 Теорема о дисперсии произведения
- •Лекция 12
- •12.1 Закон больших чисел
- •12.1.1 Неравенство Чебышева
- •12.1.2 Теорема Чебышева
- •12.1.3 Теорема Бернулли
- •12.2 Центральная предельная теорема
- •Лекция 13
- •13.1 Математическая статистика. Основные понятия
- •13.2 Оценка закона распределения
- •13.2.1 Эмпирическая функция распределения
- •13.2.2 Статистический ряд распределения
- •13.2.3 Интервальный статистический ряд
- •13.2.4 Гистограмма
- •Лекция 14
- •14.1 Точечные оценки числовых характеристик
- •14.1.1 Оценка математического ожидания
- •14.1.2 Оценка начального момента
- •14.1.3 Оценка дисперсии
- •14.1.4 Оценка центрального момента
- •14.1.5 Оценка вероятности
- •14.2 Оценка параметров распределения
- •14.3 Интервальные оценки числовых характеристик
- •14.3.1 Доверительный интервал для математического ожидания
- •14.3.2 Доверительный интервал для дисперсии
- •14.3.3 Доверительный интервал для вероятности
- •Лекция 15
- •15.1 Проверка статистических гипотез
- •15.1.1 Проверка гипотезы о равенстве вероятностей
- •15.2 Критерии согласия
- •15.2.1 Критерий Пирсона
- •15.2.2 Критерий Колмогорова
- •Лекция 16
- •16.1 Статистическая обработка двухмерных случайных величин
- •16.1.1 Оценка корреляционного момента
- •16.2.1 Гипотеза о равенстве математических ожиданий
- •16.2.2 Гипотеза о равенстве дисперсий
- •16.2.3 Гипотеза о равенстве законов распределения
- •Лекция 17
- •17.1 Оценка регрессионных характеристик
- •17.1.1 Метод наименьших квадратов
- •Практический раздел Контрольные работы Указания по выбору варианта
- •Контрольная работа №1. Теория вероятностей Задача 1. Случайные события. Вероятность события Условия вариантов задачи
- •Методические указания
- •Основные комбинаторные формулы
- •Примеры
- •Задача 2. Теоремы сложения и умножения вероятностей Условия вариантов задачи
- •Методические указания
- •Примеры
- •Задача 3. Формула полной вероятности. Формула Байеса Условия вариантов задачи
- •Методические указания
- •Примеры
- •Задача 4. Формула Бернулли Условия вариантов задачи
- •Методические указания
- •Примеры
- •Задача 5. Дискретная случайная величина Условия вариантов задачи
- •Методические указания
- •Примеры
- •Задача 6. Непрерывная случайная величина Условия вариантов задачи
- •Методические указания
- •Примеры
- •Задача 7. Закон распределения функции случайного аргумента Условия вариантов задачи
- •Методические указания
- •Примеры
- •Задача 8. Двухмерные случайные величины Условия вариантов задачи
- •Методические указания
- •Примеры
- •Задача 9. Числовые характеристики суммы и произведения случайных величин Условия вариантов задачи
- •Методические указания
- •Примеры
- •Контрольная работа №2. Математическая статистика Задача 10. Обработка одномерной выборки Условие задачи
- •Методические указания
- •Оценка закона распределения
- •Точечные оценки числовых характеристик
- •Интервальные оценки числовых характеристик
- •Проверка статистических гипотез
- •Примеры
- •Задача 11. Обработка двухмерной выборки Условие задачи
- •Методические указания
- •Оценка регрессионных характеристик
- •Примеры
- •8,74746;
- •8,86278
15.2 Критерии согласия
Критериями согласия называются критерии, используемые для проверки гипотез о предполагаемом законе распределения.
Гипотеза о законе распределения выдвигается следующим образом.
1.
Построить по вариационному ряду график
эмпирической
функции распределения
![]() и гистограммы по
интервальным статистическим рядам
(равноинтервальному и/или равновероятностному).
и гистограммы по
интервальным статистическим рядам
(равноинтервальному и/или равновероятностному).
2. По виду графиков выдвинуть двухальтернативную гипотезу о предполагаемом (гипотетическом) законе распределения:
![]() –величина
X
распределена по такому-то
закону:
–величина
X
распределена по такому-то
закону:
![]()
![]() –величина
X
не распределена по такому-то
закону:
–величина
X
не распределена по такому-то
закону:
![]()
где
![]() – плотность и функция распределения
гипотетического закона распределения.
– плотность и функция распределения
гипотетического закона распределения.
График
эмпирической
функции распределения
![]() должен быть похож на график функции
распределения
должен быть похож на график функции
распределения
![]() гипотетического закона, а гистограммы
на график плотности гипотетического
распределения
гипотетического закона, а гистограммы
на график плотности гипотетического
распределения
![]() .
.
3.
Вычислить точечные оценки математического
ожидания
![]() и
дисперсии
и
дисперсии![]() и, используя метод моментов или метод
максимального правдоподобия, определить
оценки неизвестных параметров
и, используя метод моментов или метод
максимального правдоподобия, определить
оценки неизвестных параметров
![]() гипотетического закона распределения,
где
гипотетического закона распределения,
где![]() –
число неизвестных параметров
гипотетического закона распределения.
–
число неизвестных параметров
гипотетического закона распределения.
Оценки неизвестных параметров а, b равномерного распределения можно определить по формулам
![]()
или
![]()
где
![]() –
первое и последнее значение вариационного
ряда соответственно.
–
первое и последнее значение вариационного
ряда соответственно.
Оценку неизвестного параметра экспоненциального распределения можно определить по формуле
![]()
Оценки
неизвестных параметров
![]() нормального
распределения можно определить по
формулам:
нормального
распределения можно определить по
формулам:
![]()
4. Проверить гипотезу о предполагаемом законе распределения при помощи критерия согласия.
15.2.1 Критерий Пирсона
Критерий
согласия Пирсона
(![]() )
один из наиболее часто применяемых
критериев. Алгоритм проверки гипотезы
о законе распределения следующий.
)
один из наиболее часто применяемых
критериев. Алгоритм проверки гипотезы
о законе распределения следующий.
1.
По интервальному
статистическому ряду
(равноинтервальному
или равновероятностному) вычислить
значение критерия
![]() по
формуле:
по
формуле:
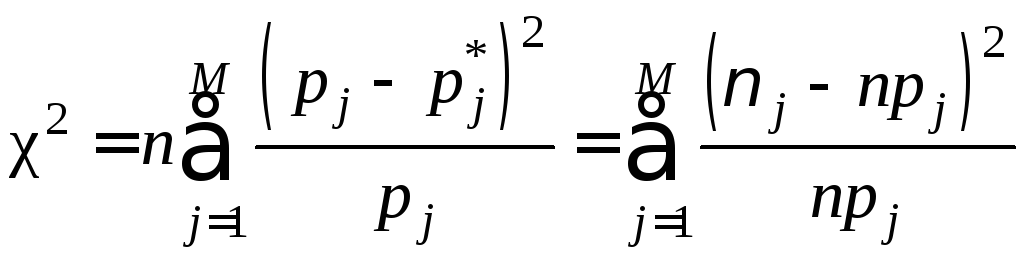 , (15.2)
, (15.2)
где
![]() –
объем выборки;
–
объем выборки;
M – число интервалов интервального статистического ряда;
![]() –частота
попадания в j-й
интервал;
–частота
попадания в j-й
интервал;
![]() –количество
чисел в выборке, попадающих в j-й
интервал;
–количество
чисел в выборке, попадающих в j-й
интервал;
pj
–
теоретическая вероятность попадания
случайной величины в j-
й интервал при условии, что гипотеза
![]() верна:
верна:
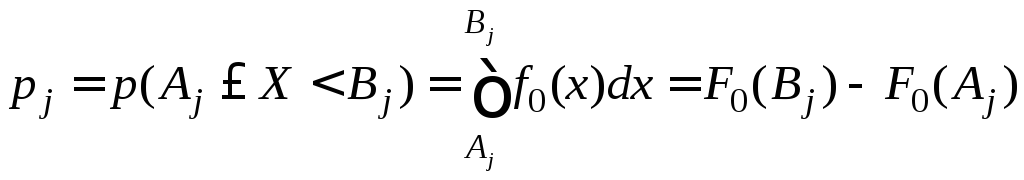 . (15.3)
. (15.3)
где
![]() ,
,![]() –
плотность и функция распределения
гипотетического закона распределения.
–
плотность и функция распределения
гипотетического закона распределения.
При расчете p1 и pM в качестве крайних границ первого и последнего интервалов A1, BM следует использовать теоретические границы гипотетического закона распределения.
Величина
![]() распределена по закону, который
называется распределением
распределена по закону, который
называется распределением![]() .
Данное распределение не зависит от
закон распределения величиныX,
а зависит от параметра k,
который называется числом степеней
свободы:
.
Данное распределение не зависит от
закон распределения величиныX,
а зависит от параметра k,
который называется числом степеней
свободы:
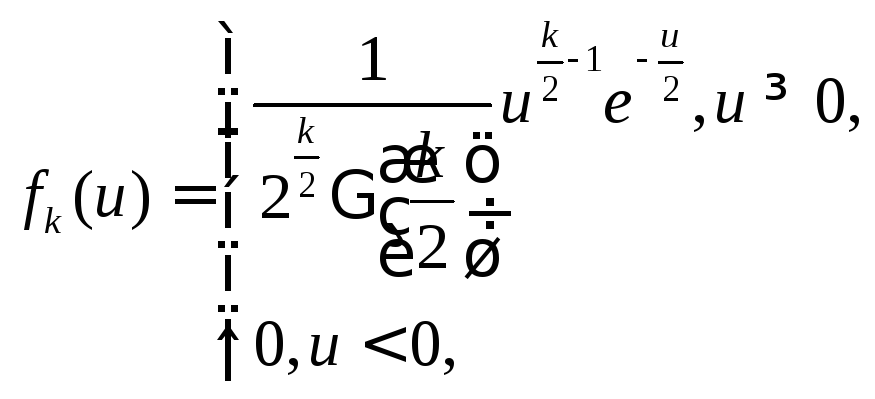 (15.4)
(15.4)
где
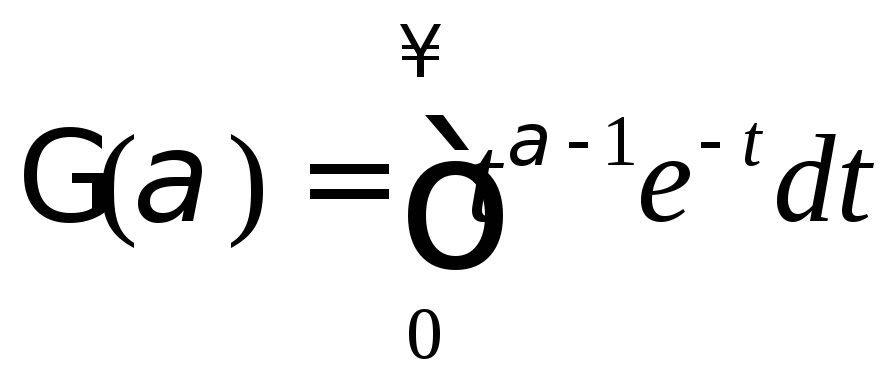 - гамма-функция.
- гамма-функция.
Так
как аналитическое выражение плотности
распределения
![]() является
довольно сложным, то в практике используют
таблицу значений
является
довольно сложным, то в практике используют
таблицу значений![]() ,
,
рассчитанных
из уравнения
![]() ,
для различных значенийk.
,
для различных значенийk.
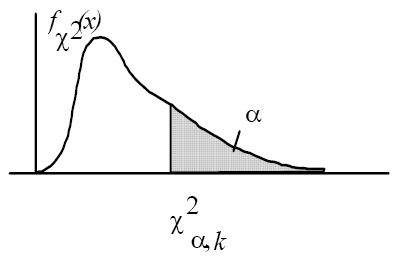
2.
Из таблицы распределения![]() выбирается значение
выбирается значение
![]() ,
где a
- заданный уровень значимости (a
= 0,05 или a
=
0,01), а k
- число степеней свободы, которое
определяется по формуле
,
где a
- заданный уровень значимости (a
= 0,05 или a
=
0,01), а k
- число степеней свободы, которое
определяется по формуле
![]() ,
,
где M – число слагаемых в формуле (15.2), т.е. число интервалов интервального статистического ряда,
s - число неизвестных параметров гипотетического закона распределения, оценки которых были определены по исходной выборке.
3.
Если значение![]() ,
вычисленное по формуле (15.2), больше, чем
критическое значение, т.е.
,
вычисленное по формуле (15.2), больше, чем
критическое значение, т.е.
![]() ,
то гипотезаH0
отклоняется, в противном случае нет
оснований ее отклонить.
,
то гипотезаH0
отклоняется, в противном случае нет
оснований ее отклонить.
