Лабораторная работа №3 Множественная регрессия

Линейная множественная регрессия:

Степенная функция:

Экспонента:

Гипербола:

Оценка параметров линейной множественной регрессии

1) в натуральном масштабе, т.е. для уравнения система нормальных уравнений имеет вид:

Ее решение может быть найдено, например, методом определителей.

Вычисление параметров линейной множественной регрессии можно провести с помощью инструмента Сервис/Анализ данных/Регрессия.

2) в стандартизированном масштабе:

,

где – стандартизированные переменные

;

,

–стандартизированные коэффициенты регрессии. Решают систему нормальных уравнений вида

Решая ее методом определителей, найдем -коэффициенты.

Определение-коэффициентов:

1) Находим матрицу парных коэффициентов корреляции. Для двухфакторной линейной регрессии она имеет вид:

	y
y	1
		1
			1

Удобнее всего найти эту матрицу Excel, используя инструмент анализа данных Корреляция. Для этого в главном меню нужно последовательно выбрать Сервис/Анализ данных/Корреляция.

2) для стандартизированного уравнения регрессии

имеем

; .

Коэффициенты «чистой» регрессии связаны с -коэффициентами следующим образом:

.

Методика построения уравнения регрессии при двухфакторном регрессионном анализе

приводит к следующим формулам для оценки параметров:

, ,.

Методика построения уравнения регрессии в виде степенной функции

Преобразуем ее в линейный вид:

,

где переменные выражены в логарифмах. Далее процедура МНК такая же, что и описана выше: строится система нормальных уравнений и определяются параметры, которые затем следует потенцировать.

Оценка тесноты связи и статистической значимости во множественной регрессии

1) коэффициент множественной детерминации ,

;

2) индекс множественной корреляции R;

3)линейный коэффициент множественной корреляции (для )

;

4)в случае двухфакторной линейной модели индекс множественной корреляции R может быть найден по формуле:

.

5) Скорректированный индекс (коэффициент) корреляции:

; k – число параметров при переменных.

В статистических пакетах прикладных программ в процедуре множественной регрессии обычно приводится скорректированный коэффициент (индекс) множественной корреляции (детерминации).

6) дельта-коэффициенты :

,

где – коэффициент парной корреляции междуy и ;

–множественный коэффициент детерминации.

7) частные коэффициенты эластичности:

,

где – коэффициент «чистой» регрессии при факторе;

–среднее значение результативного признака;

–среднее значение признака .

Значимость уравнения множественной регрессии в целом

оценивается с помощью F-критерия Фишера:

,

где n – число наблюдений, m – число параметров при переменной x. Если расчетное значение критерия с истепенями свободы больше табличного при заданном уровне значимости, то модель считается значимой.

Прогнозирование по уравнению линейной множественной регрессии

где– ошибка прогнозного значения, вычисляемая по формуле

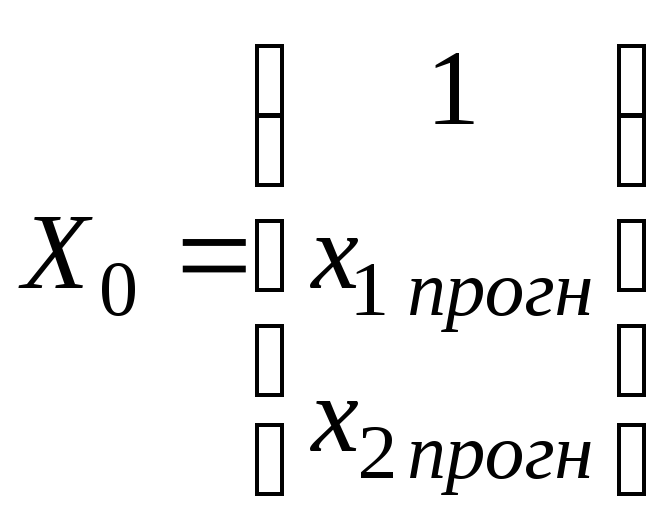
для двухфакторной модели.

Мерой для оценки включения фактора в модель

служит частный F-критерий, т.е. . Так, если оцениваем значимость влияния факторапосле включения в модель факторов, то формула частногоF-критерия примет вид:

.

Если фактическое значение критерия с истепенями свободы больше табличного при заданном уровне значимости, то дополнительное включение факторав модель статистически оправдано и коэффициент регрессии при данном факторе статистически значим.

Оценка значимости коэффициентов «чистой» регрессии

Для каждого фактора используется формула

,

где – коэффициент «чистой» регрессии при факторе;– средняя квадратическая ошибка коэффициента регрессии,

,

где – среднее квадратическое отклонение для признакаy;

–коэффициент детерминации для уравнения множественной регрессии;

–среднее квадратическое отклонение для признака ;

–коэффициент детерминации для зависимости фактора со всеми другими факторами уравнения множественной регрессии.

Практические рекомендации по выполнению расчетов

с помощью табличного редактора MS Excel

Исследуется зависимость производительности труда y (т/ч) от уровня механизации работ (%), среднего возраста работников(лет) и энерговооруженности(кВт/100 работающих) по данным 14 промышленных предприятий.

	32	30	36	40	41	47	56	54	60	55	61	67	69	76
	33	31	41	39	46	43	34	38	42	35	39	44	40	41
	300	290	350	400	400	480	500	520	590	540	600	700	700	750
y	20	24	28	30	31	33	34	37	38	40	41	43	45	48

Необходимо:

1. Рассчитать параметры линейного уравнения множественной регрессии с полным перечнем факторов.

2. Оценить значимость уравнения в целом, используя значение множественного коэффициента корреляции и общего F-критерия Фишера.

3. Оценить статистическую значимость параметров регрессионной модели с помощью t-критерия.

4. Исследовать коллинеарность между факторами. При наличии мультиколлинеарности исключить какой-либо фактор из уравнения регрессии.

5. Построить новое уравнение множественной регрессии, провести все необходимые исследования, аналогичные проведенным выше.

6. На основании результатов п. 5 найти

а) средние коэффициенты эластичности фактора y от независимых факторов;

б) прогнозное значение результата при значении важнейшей объясняющей переменной, равном максимальному наблюденному значению, увеличенному на 10 %, и при значении второй объясняющей переменной, равном минимальному наблюденному значению, уменьшенному на 15%.

в) Интервальное предсказание значения y с надежностью 0,95.

1. Получение протокола расчета. Операция проводится с помощью инструмента Анализ данных/Регрессия. Она аналогична расчету параметров парной линейной регрессии, рассмотренной выше, только в отличие от парной регрессии при заполнении строки входной интервал X в диалоговом окне следует указать сразу все столбцы значений факторных переменных.

Результаты анализа имеют вид:

ВЫВОД ИТОГОВ
Регрессионная статистика
Множественный R	0,97517313
R-квадрат	0,950962633
Нормированный R-квадрат	0,936251423
Стандартная ошибка	2,038864298
Наблюдения	14
Дисперсионный анализ
	df	SS	MS	F
Регрессия	3	806,1446094	268,7148698	64,64204
Остаток	10	41,56967627	4,156967627
Итого	13	847,7142857
	Коэффициенты	Стандартная ошибка	t-статистика
Y-пересечение	5,711742473	6,18918556	0,922858495
x1	0,148601283	0,340417689	0,436526326
x2	0,064880259	0,162051974	0,400366976
x3	0,037784221	0,033824423	1,11706919

2. Оцениваем статистическую значимость в целом. Изучив результаты, отмечаем, что в целом полученное уравнение линейной множественной регрессии

является статистически значимым. Действительно, . Сравним это число с критическим значением критерия Фишера, полученным при числе степеней свободыи, гдеn – число наблюдений, m – число параметров при переменной x. В нашем случае ,. Критическое значение даст функцияFРАСПОБР. , что существенно меньше расчетного значения.

О доле вариации результативного признака y, объясненной построенным уравнением множественной регрессии лучше всего судить по значению нормированного коэффициента корреляции, в данном случае он равен 0,9363. То есть построенное уравнение объясняет почти 94% всей вариации признака y.

3. Оцениваем статистическую значимость по отдельным параметрам. Чтобы оценить статистическую значимость параметров регрессионной модели с помощью t-критерия, найдем соответствующее нашим параметрам критическое значение с помощью функции СТЬЮДРАСПОБР при заданном уровне значимости 0,05 и числе степеней свободы . Коэффициент признается значимым, если выполняется неравенство.

Имеем

	0,44	0,4	1,12
	2,2281

Таким образом, ни один из факторов не имеет статистически значимого коэффициента регрессии, и построенное уравнение для прогнозирования непригодно.

4. Исследуем коллинеарность между факторами. Матрицу парных коэффициентов корреляции можно получить, используя инструмент Анализ данных/Корреляция. Заполнив диалоговое окно,

получим следующий результат:

Для оценки мультиколлинеарности факторов вычислим определитель матрицы парных коэффициентов корреляции факторов.

.

Поскольку определитель матрицы межфакторной корреляции близок к нулю, имеем мультиколлинеарность факторов и вытекающую отсюда ненадежность результатов множественной регрессии.

Оценка значимости мультиколлинеарности факторов может быть проведена методом испытания гипотезы о независимости переменных, т.е. . Доказано, что величинаимеет приближенное распределениес числом степеней свободы. Если фактическое значениепревосходит табличное (критическое), то гипотезаотклоняется, и мультиколлинеарность считается доказанной.

Имеем .

Критическое значение можно найти через статистическую функциюХИ2ОБР(), где– уровень значимости (по условию 0,05), аn – число степеней свободы. В нашем случае степеней свободы . Получаем.. Мультиколлинеарностью факторов пренебречь нельзя.

Особенно высока коллинеарность факторов и,. Один из этих факторов следует исключить из уравнения регрессии. Логично исключить тот, который имеет меньший коэффициент парной корреляции. Поскольку, а, исключаем фактор.

5. Построим регрессию на факторах и.

ВЫВОД ИТОГОВ
Регрессионная статистика
Множественный R	0,974693901
R-квадрат	0,950028201
Нормированный R-квадрат	0,940942419
Стандартная ошибка	1,962415214
Наблюдения	14
Дисперсионный анализ
	df	SS	MS	F
Регрессия	2	805,3524775	402,6762388	104,5621
Остаток	11	42,3618082	3,851073473
Итого	13	847,7142857
	Коэффициенты	Стандартная ошибка	t-статистика
Y-пересечение	7,265656067	4,873196972	1,490942416
x2	0,031021017	0,136948082	0,226516625
x3	0,052435862	0,004030875	13,00855684

Получили результаты:

, ,, что много больше, чем.

	0,22	13
	2,2281

Таким образом, при весьма удовлетворительной значимости уравнения регрессии в целом, мы добились значимости коэффициента регрессии при переменной .

6.

а) Найдем коэффициенты эластичности:

, (6.18)

где – коэффициент «чистой» регрессии при факторе;

–среднее значение результативного признака;

–среднее значение признака .

Имеем

	y
Среднее	35,14285714	39	508,5714286
Эластичность

Таким образом, при изменении фактора (среднего возраста работников) на 1%, производительность возрастает незначительно, на 0,03%; при изменении фактора (энерговооруженности) на 1%, производительность труда увеличивается на 0,72%.

б) Выполним прогнозирование. Максимальное наблюденное значение фактора – 750. Минимальное значение фактора –31. Прогнозные значения факторов:

; .

Тогда .

в) Доверительный интервал для данного прогнозного значения y можно найти, зная предельную ошибку прогноза , где– соответствующее критическое значение критерия Стьюдента, а– ошибка прогнозного значения. В нашем случае.

Ошибку прогнозного значения функции регрессии получим по формуле

.

Шаг 1. Параметр S – стандартная ошибка регрессии приведен в последней регрессионной статистике .

Шаг 2. Матрица состоит из чисел:. То есть,

.

Шаг 3. Матрица X состоит из чисел .

Составляем вспомогательную таблицу:

	…..	…..	….	…..	…..
Сумма

В данном случае, .

Шаг 4. Транспонируем матрицу X. Поскольку она симметрическая, то

.

Шаг 5. Найдем произведение матриц . ВExсel это можно сделать с помощью функции МУМНОЖ.

	58537523,04	2158299716	29989312607
	2158299716	79577299061	1,10572E+12
	29989312607	1,10572E+12	1,53641E+13

Шаг 6. Найдем обратную матрицу к матрице произведения . ВExсel это можно сделать с помощью функции МОБР.

	0,281568563	-0,007773123	9,81695E-06
	-0,007773123	0,000215175	-3,13231E-07
	9,81695E-06	-3,13231E-07	3,38079E-09

Шаг 7. Найдем произведение матриц (размерность матрицы произведения).

0,083373216

-0,002314683

3,84533E-06

Шаг 8. Найдем произведение матриц (размерность матрицы произведения, то есть только одно число).

.

Шаг 9. .

Шаг 10. .

Шаг 11. Таким образом, прогнозное значение результата будет с вероятностью 95% находиться в интервале .

Задания для самостоятельной работы

Вариант 1

x1	32	30	36	40	41	47	56	54	60	55	61	67	69	76
x2	33	31	41	39	46	43	34	38	42	35	39	44	40	41
x3	30	29	35	40	40	48	50	52	59	54	60	70	70	75
y	20	24	28	30	31	33	34	37	38	40	41	43	45	48

Вариант 2

x1	55	46	40	39	35	29	31	75	68	66	60	54	59	53
x2	33	42	45	38	40	30	32	40	39	43	38	34	41	37
x3	50	45	39	40	34	30	30	74	69	66	59	54	60	52
y	33	32	30	29	27	23	19	47	44	42	40	39	37	36

Вариант 3

x1	48	57	55	61	56	62	68	70	77	42	41	37	31	33
x2	44	35	39	43	36	40	45	41	42	47	40	42	32	34
x3	47	56	54	62	56	62	67	70	76	42	40	37	30	32
y	34	35	38	39	41	42	44	46	49	32	31	29	25	21

Вариант 4

x1	52	54	45	39	38	34	28	30	74	67	65	59	53	58
x2	36	32	41	44	37	39	29	31	39	38	42	37	33	40
x3	52	53	45	38	38	34	28	31	73	66	65	60	52	57
y	35	32	31	29	28	26	22	18	46	43	41	39	33	36

Вариант 5

x1	43	49	58	56	62	57	63	69	71	78	34	32	38	42
x2	48	45	36	40	44	37	41	46	42	43	35	33	43	41
x3	42	48	58	55	61	56	62	70	70	78	35	32	38	41
y	33	35	36	39	40	42	43	45	47	50	22	26	30	32

Вариант 6

x1	52	57	51	53	44	38	37	33	27	29	73	66	64	58
x2	32	39	35	31	40	43	36	38	28	30	38	37	41	36
x3	52	56	50	53	45	37	37	32	28	30	72	66	64	59
y	37	35	34	31	30	28	27	25	21	17	45	42	40	38

Вариант 7

x1	39	43	44	50	59	57	63	58	64	70	72	79	35	33
x2	44	42	49	46	37	41	45	38	42	47	43	44	36	34
x3	45	42	50	46	38	40	45	39	41	48	43	44	35	34
y	31	33	34	36	37	40	41	43	44	46	48	51	23	27

Вариант 8

x1	63	57	51	56	50	52	43	37	36	32	26	28	72	65
x2	40	35	31	38	34	30	39	42	35	37	27	29	37	36
x3	39	38	35	35	32	31	28	28	25	25	21	15	45	40
y	39	37	36	34	33	30	29	27	26	24	20	16	44	41

Вариант 9

x1	64	59	65	71	73	80	36	34	40	44	45	51	60	58
x2	46	39	43	48	44	45	37	35	45	43	50	47	38	42
x3	50	40	50	55	50	60	35	34	42	41	48	49	50	50
y	42	44	45	47	49	52	24	28	32	34	35	37	38	41

Вариант 10

x1	46	52	61	59	65	60	66	72	74	81	37	35	41	45
x2	51	48	39	43	47	40	44	49	45	46	38	36	46	44
x3	46	52	60	58	64	61	65	72	74	80	38	34	40	44
y	36	38	39	42	43	45	46	48	50	53	25	29	33	35