
- •I частина
- •§2. Способи задання функції
- •§3. Властивості функцій
- •§4. Елементарні функції
- •Розділ 2 границя функції. Похідна
- •§1. Границя функції
- •§2. Похідна функції
- •§3. Диференціювання складених функцій
- •§4. Похідні вищих порядків
- •§5. Застосування похідної для знаходження інтервалів монотонності та екстремумів функції
- •§6. Дослідження функції на опуклість, угнутість.
- •§7. Схема дослідження функції
- •§8. Функція багатьох змінних. Частинні похідні функції багатьох змінних. Частинні похідні вищих порядків
- •Розділ 3 диференціал функції
- •§1. Визначення диференціала функції однієї змінної
- •§2. Частинний і повний диференціали для функції багатьох змінних. Диференціали вищих порядків
- •§3. Абсолютна та відносна похибка прямого і посереднього (непрямого) виміру. Застосування диференціалів для визначення похибок вимірювань
- •§4. Застосування диференціала для лінійної апроксимації функції та наближених обчислень
- •Контрольні питання
§4. Застосування диференціала для лінійної апроксимації функції та наближених обчислень
Раніше
ми визначили, що різниця
![]() - нескінченно мала вищого порядку
малості, ніж
- нескінченно мала вищого порядку
малості, ніж![]() ,
тому при досить малому
,
тому при досить малому![]() :
:
![]() . (16)
. (16)
Це означає,
що при малих змінах аргументу (від
початкового значення
![]() )
величину зміни функції
)
величину зміни функції![]() можна приблизно вважати пропорційній
величині зміни аргументу з коефіцієнтом
пропорційності, рівним значенню похідної
можна приблизно вважати пропорційній
величині зміни аргументу з коефіцієнтом
пропорційності, рівним значенню похідної![]() ;
криву
;
криву![]() при цьому можна приблизно замінити
дотичною до неї в околі точки
при цьому можна приблизно замінити
дотичною до неї в околі точки![]() .
Так як
.
Так як![]() ,
то
,
то![]() .
Таким чином:
.
Таким чином:
![]() , (17)
, (17)
або:
![]() . (18)
. (18)
Розглянемо на прикладах застосування даної наближеної рівності для лінійної апроксимації деяких елементарних функцій і наближених обчислень.
Приклади.
№1.
Обчислити
![]() .
.
Розв’язання.
У нашому прикладі маємо
функцію
![]() .
Треба знайти значення функції
.
Треба знайти значення функції![]() ,
де
,
де![]() і
і![]() .
.
Так як
![]() то
то![]() .
.
Отже,
![]() .
.
№2.
Обчислити
![]() .
.
Розв’язання.
У нашому прикладі маємо
функцію
![]() .
Треба знайти значення функції
.
Треба знайти значення функції![]() ,
де
,
де![]() і
і![]() .
.
![]() .
.
Отже,
![]() .
.
№3.
Обчислити
![]() .
.
Розв’язання.
У нашому прикладі маємо
функцію
![]() .
Треба знайти значення функції
.
Треба знайти значення функції![]() ,
де
,
де![]() ,
,![]() ,
,![]() .
.
![]() .
.
При
![]() :
: .
.
Отже,
![]() .
.
№4.
Знайти
наближене значення вираження
![]() .
.
Розв’язання.
Маємо функцію двох
змінних
![]() .
.
Треба знайти
значення функції
![]() ,
,
де
![]() ,
,![]() ,
,![]() і
і![]() ,
,![]() ,
,![]() .
.
![]() ,
,
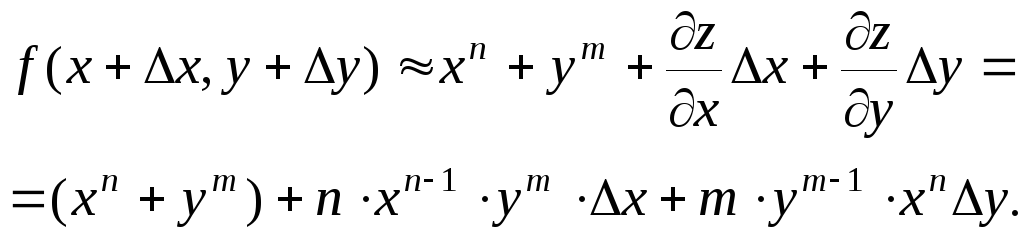
При
![]() і
і![]() :
:
 .
.
Отже:

№5.
Знайти площу
кімнати, якщо довжина і ширина кімнати
були виміряні з наступною точністю:
![]() (м) і
(м) і![]() (м).
(м).
Розв’язання. Площу кімнати можна визначити за формулою:
![]() .
.
Так, як площа
![]() ,
то
,
то![]() м2.
м2.
Знайдемо
абсолютну похибку непрямого виміру для
функції двох змінних
![]() :
:
![]() ;
;
![]() .
.
Отже:
![]() .
.
Контрольні питання
Функція однієї незалежної змінної. Область визначення, область значень функції. Способи задання функції. Обернена функція. Властивості функцій (парність і непарність, періодичність, монотонність, опуклість і угнутість).
Графіки і властивості основних елементарних функцій (степеневої
 ,
лінійної
,
лінійної ,
показникової
,
показникової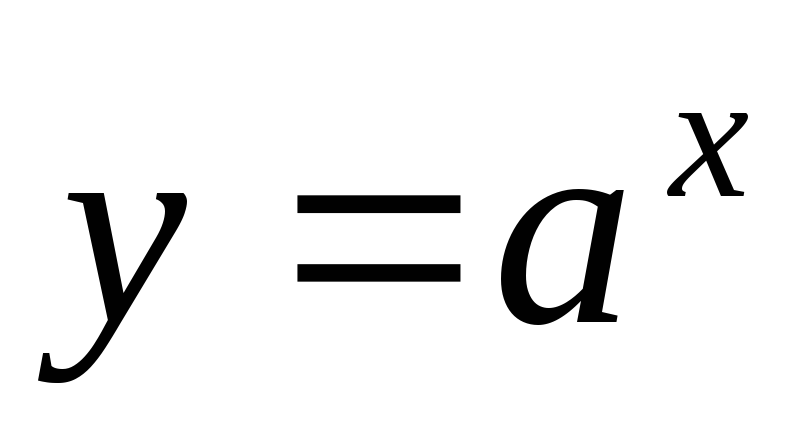 ,
логарифмічної
,
логарифмічної ,
тригонометричних функцій:
,
тригонометричних функцій: ).
).Границя функції. Визначення нескінченно малої і нескінченно великої функції. Теореми про границі функції. Перша і друга чудові границі.
Визначення похідної функції. Фізична і геометрична інтерпретація похідної функції в точці.
Диференціювання складених функцій.
Похідні вищих порядків.
Застосування похідної для дослідження функції. Інтервали зростання й спадання функції, екстремуми. Опуклість і угнутість кривої, точки перегину.
Схема дослідження функції. Побудова графіків функцій.
Функція багатьох змінних.
Частинні похідні функції багатьох змінних.
Частинні похідні вищих порядків.
Диференціал функції, його аналітичний і геометричний зміст. У яких випадках можна заміняти приріст функції її диференціалом?
Загальний вигляд задачі, яку розв'язують заміною приросту функції її диференціалом.
Застосування методів наближених обчислень для розрахунків основних елементарних функцій:
 ,
, ;
; ;
; .
.Прямі вимірювання. Абсолютна і відносна похибки прямих вимірювань.
Посередні (непрямі) вимірювання. Абсолютна і відносна похибки посередніх вимірювань для випадку: функції однієї незалежної змінної; функції багатьох незалежних змінних.
