
- •I частина
- •§2. Способи задання функції
- •§3. Властивості функцій
- •§4. Елементарні функції
- •Розділ 2 границя функції. Похідна
- •§1. Границя функції
- •§2. Похідна функції
- •§3. Диференціювання складених функцій
- •§4. Похідні вищих порядків
- •§5. Застосування похідної для знаходження інтервалів монотонності та екстремумів функції
- •§6. Дослідження функції на опуклість, угнутість.
- •§7. Схема дослідження функції
- •§8. Функція багатьох змінних. Частинні похідні функції багатьох змінних. Частинні похідні вищих порядків
- •Розділ 3 диференціал функції
- •§1. Визначення диференціала функції однієї змінної
- •§2. Частинний і повний диференціали для функції багатьох змінних. Диференціали вищих порядків
- •§3. Абсолютна та відносна похибка прямого і посереднього (непрямого) виміру. Застосування диференціалів для визначення похибок вимірювань
- •§4. Застосування диференціала для лінійної апроксимації функції та наближених обчислень
- •Контрольні питання
Розділ 2 границя функції. Похідна
§1. Границя функції
Число
А
називається границею
функції
![]() прих,
що
прямує до
а (х
а),
якщо для будь-якого як завгодно малого
числа
прих,
що
прямує до
а (х
а),
якщо для будь-якого як завгодно малого
числа
![]() знайдеться таке мале число
знайдеться таке мале число![]() ,
що для всіхх,
які задовольняють умову
,
що для всіхх,
які задовольняють умову
![]() ,
виконується нерівність
,
виконується нерівність
![]() .
.
Границю функції записують у вигляді:
![]()
 . (1)
. (1)
Іншими словами, коли значення аргументу прямує до числа а, то значення функції прямує до значення А. Значення функції в точці а може бути рівним значенню границі функції в точці а, але може і не дорівнювати (дивись рис.12).
Функція
![]() називається нескінченно
великою при
х
що
прямує
до
а,
якщо її границя рівна нескінченості
(
називається нескінченно
великою при
х
що
прямує
до
а,
якщо її границя рівна нескінченості
(![]() ).
Або, якщо значення функції більше
довільного додатного числаМ:
(
).
Або, якщо значення функції більше
довільного додатного числаМ:
(![]() ).
).
Функція
(х)
називається нескінченно
малою при
х
а
якщо її границя рівна нулю(![]() ).
).
Практичне обчислення границь базується на теоремах про границі.
Якщо
існують
![]() та
та![]() тоді:
тоді:
1) ![]() ;
;
2) ![]() ;
;
3) 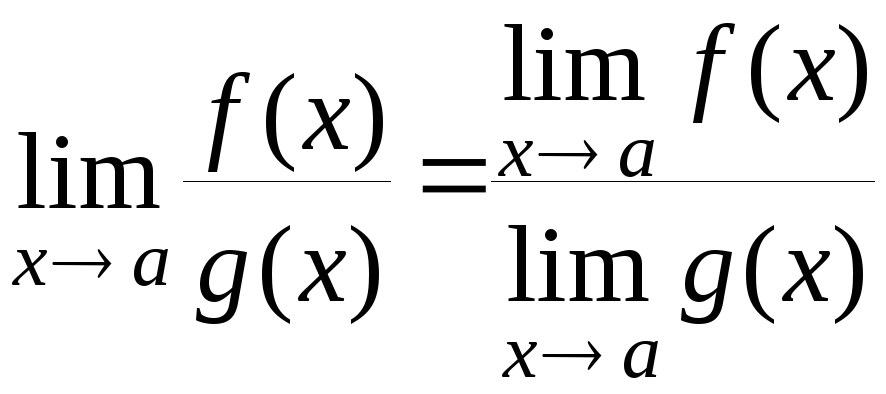 ,
при
,
при![]() .
.
Використовуються також наступні границі:
 (перша
чудова границя); (2)
(перша
чудова границя); (2)
![]()
![]()
![]() (друга
чудова границя). (3)
(друга
чудова границя). (3)
Приклади.
№1.
Знайти
границю функції:
![]() .
.
Розв’язання.
Якщо
замість змінної х
підставити у вираз значення 6:
![]() ,то
одержимо
невизначеність
типу
,то
одержимо
невизначеність
типу
![]() .
Розкриємо її. Для цього представимо
чисельник і знаменник дробу у вигляді
добутків:
.
Розкриємо її. Для цього представимо
чисельник і знаменник дробу у вигляді
добутків:
![]() .
.
№2.
Знайти
границю функції:
![]() .
.
Розв’язання.
Якщо
замість змінної х
підставити у вираз значення нескінченності
:
![]() ,то
одержимо
невизначеність
типу
,то
одержимо
невизначеність
типу
![]() .
Розкриємо її. Для цього винесемо за
дужки
.
Розкриємо її. Для цього винесемо за
дужки![]() :
:
 .
.
Якщо
тепер замість змінної х
підставити у вираз значення ,
то
вираз, вигляду
![]() прямує до нуля. В результаті:
прямує до нуля. В результаті:
 .
.
№3.
Знайти
границю функції
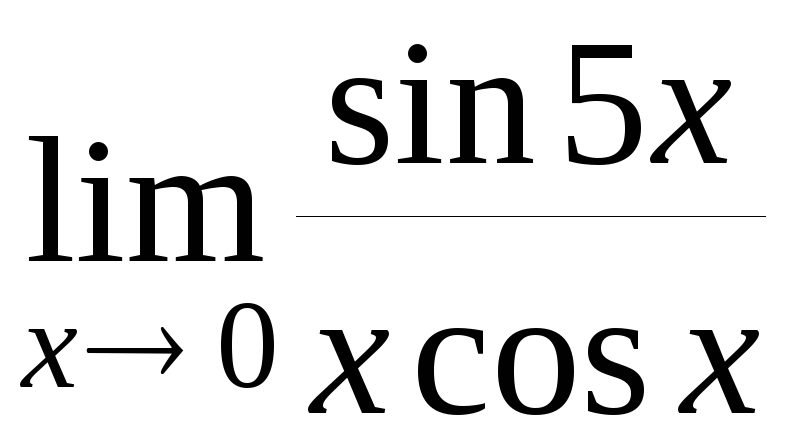 .
.
Розв’язання.
Помножимо
чисельник і знаменник дробу на
![]() .
.

§2. Похідна функції
Нехай
маємо функцію
![]() .
Дамо аргументу х
приріст
х.
Одержимо
нове значення аргументу х+х.
Відповідні
цим значенням аргументу значення функції
можна записати у вигляді:
.
Дамо аргументу х
приріст
х.
Одержимо
нове значення аргументу х+х.
Відповідні
цим значенням аргументу значення функції
можна записати у вигляді:
![]() і
і
![]() .
.
Різниця
значень функції
![]() (або
(або
![]() )
називаєтьсяприростом
функції
на відрізку
х; х+х
(дивись рис. 13).
)
називаєтьсяприростом
функції
на відрізку
х; х+х
(дивись рис. 13).
П охідною
від функції
охідною
від функції
![]() по
аргументу х
називається границя відношення приросту
функції до приросту аргументу, коли
приріст аргументу прямує до нуля:
по
аргументу х
називається границя відношення приросту
функції до приросту аргументу, коли
приріст аргументу прямує до нуля:
![]() або
або
![]() . (4)
. (4)
Похідна
позначається також
![]() .
.
Геометрична інтерпретація похідної функції в точці.
З образимо
графік довільної функції
образимо
графік довільної функції
![]() (дивись рис. 14).
На осі Ox
візьмемо
точку х0.
Знайдемо
значення функції
в
цій точці:
(дивись рис. 14).
На осі Ox
візьмемо
точку х0.
Знайдемо
значення функції
в
цій точці:
![]() .Дамо
аргументу приріст х
і
одержимо
точку х0+х.
Відповідно,
функція прийме значення:
.Дамо
аргументу приріст х
і
одержимо
точку х0+х.
Відповідно,
функція прийме значення:
![]() .Позначимо
точки
.Позначимо
точки
![]() і
і![]() .
.
Проведемо
через ці точки січну пряму
![]() .
Вона нахилена до додатного напрямку
осіОх
під
кутом
.
Вона нахилена до додатного напрямку
осіОх
під
кутом
![]() .
Через точкуМ
проведемо
пряму, паралельну осі Ох.
Позначимо
точку перетину цієї прямої з перпендикуляром
із точки
.
Через точкуМ
проведемо
пряму, паралельну осі Ох.
Позначимо
точку перетину цієї прямої з перпендикуляром
із точки
![]() як точкуN.
Зі
співвідношення в прямокутному трикутнику
як точкуN.
Зі
співвідношення в прямокутному трикутнику
![]() маємо:
маємо:![]() .
Коли
.
Коли![]() точкаМ’
переміщається уздовж кривої, наближаючись
до точки
М. Січна
повертається навколо точки М
і в граничному положенні січна збіжиться
з дотичною.
точкаМ’
переміщається уздовж кривої, наближаючись
до точки
М. Січна
повертається навколо точки М
і в граничному положенні січна збіжиться
з дотичною.
Кутовий
коефіцієнт дотичної дорівнює
![]() .
Таким чином, при
.
Таким чином, при![]() кут
кут![]() наближається до кута
наближається до кута![]() і
і
![]() (5)
(5)
Геометрична
інтерпретація
полягає
в тому, що похідна функції в точці х0
являє
собою кутовий коефіцієнт дотичної до
графіка функції у=f(х)
у точці х0,
тобто
![]() (дивись рис. 15).
(дивись рис. 15).

Фізична інтерпретація похідної.
Нехай
тіло рухається прямолінійно за відомим
законом
![]() .
Середня швидкість за час
.
Середня швидкість за час![]() визначається за формулою:
визначається за формулою:
![]() . (6)
. (6)
Миттєва швидкість прямолінійного руху дорівнює границі цього співвідношення, тобто похідній шляху за часом руху.
![]() . (7)
. (7)
Знаходження похідної називається диференціюванням.
Правила диференціювання.
Якщо
![]() ,
,![]() - функції, залежні від
- функції, залежні від![]() ,
і можуть бути диференційовані, тоді:
,
і можуть бути диференційовані, тоді:
 ; (8)
; (8) ; (9)
; (9) . (10)
. (10)Таблиця знаходження похідних елементарних функцій.
|
1.
|
10.
|
|
2.
|
11.
|
|
3.
|
12.
|
|
4.
|
13.
|
|
5.
|
14.
|
|
6.
|
15.
|
|
7.
|
16.
|
|
8.
|
17.
|
|
9.
|
18.
|
Приклади.
№1.
Знайти
приріст функції![]() ,
при
,
при![]() .
.
Розв’язання.
![]() .
.
Відкриємо дужки і приведемо подібні доданки:
![]()
Якщо
підставити значення
![]() та
та![]() в останній вираз, то отримаємо:
в останній вираз, то отримаємо:
![]() .
.
№2.
Знайти
похідну функції
![]() .
.
Розв’язання.
![]() .
.
№3.
Знайти
похідну функції
![]() .
.
Розв’язання.
![]() =
=
![]() .
.
