21

ФЕДЕРАЛЬНОЕ АГЕНСТВО ПО ОБРАЗОВАНИЮ

ГОУ ВПО «Тульский Государственный Университет»

Кафедра «Инструментальные и метрологические системы»

МЕТРОЛОГИЯ, СТАНДАРТИЗАЦИЯ И СЕРТИФИКАЦИЯ

Лабораторная работа № М-2

ОЦЕНКА РЕЗУЛЬТАТОВ НЕСКОЛЬКИХ СЕРИЙ ИЗМЕРЕНИЙ

Тула 2005 г.

Разработали: Сотова Б.И., к.т.н., доц.

Мелай А.М., к.т.н., доц.

Соловьев С.И., к.т.н., доц.

Анисимова М.А., к.т.н., доц.

Рассмотрено на заседании каф. ИМС 17.11.04

Зав. каф. О.И.Борискин

1. Цель работы

получение практических навыков выполнения измерений;

• ознакомление с вероятностным подходом к оценке результатов измерений;

• получение навыков обработки результатов нескольких серий измерений;

2. Теоретические положения

2.1. Оценка результатов измерений как случайных величин

При проведении с одинаковой тщательностью и в одинаковых условиях повторных измерений одной и той же неизменяющейся величины мы получаем результаты, некоторые из которых отличаются друг от друга, а некоторые совпадают. Такие результаты говорят о наличии в них случайных погрешностей, то есть погрешностей, изменяющихся хаотически, непредсказуемо.

Рассмотрение случайных погрешностей (и, соответственно, результатов однократных измерений) как случайных событий дает основание использовать математический аппарат теории вероятностей и математической статистики для оценки случайных погрешностей и нахождения значения измеряемой величины, более близкого к истинному значению, чем результат одного измерения.

Теория вероятностей называет случайным такое событие, которое может произойти или не произойти. Применительно к измерениям можно сказать, что при повторных измерениях в одинаковых условиях каждая из множества возможных незначительных причин случайных изменений результатов может или появиться, или не появиться. Количественная оценка объективной возможности появления события называется его вероятностью. Вероятность достоверного события равна 1, а вероятность невозможного события - 0. Эти события неслучайные; для случайных событий вероятности их появления больше нуля и меньше единицы.

Наиболее универсальным способом описания случайных величин (в том числе результатов измерений и случайных погрешностей) являются законы распределения вероятности. Законом распределения вероятности случайной величины называется всякое соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями.

Если на процесс измерения действуют несколько влияющих факторов, а вклад каждого из факторов незначителен по сравнению с их суммарным воздействием, то, согласно центральной предельной теореме теории вероятностей, результат измерения физической величины X подчиняется нормальному закону, или закону Гаусса.

На рис. 1 показаны кривые плотности вероятности, или дифференциальной функции нормального распределения. Аналитически эта функция описывается выражением

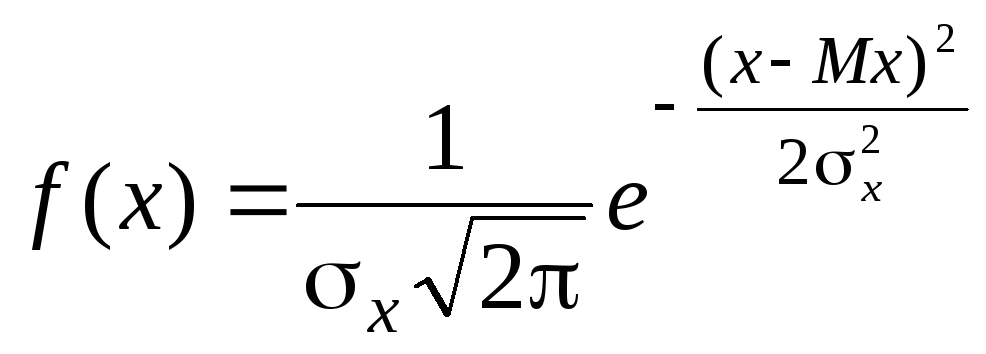, (1)

где Мх - математическое ожидание случайной величины Х

_x - среднее квадратическое отклонение (СКО) случайной величины

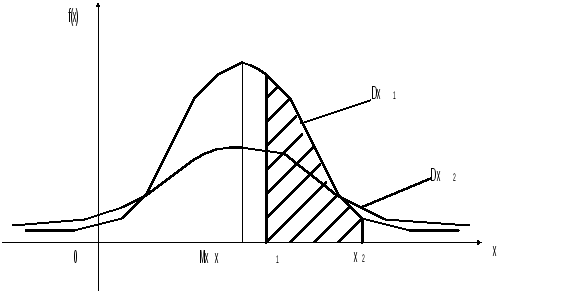
Рисунок 1 – Кривые функций нормального распределения

Математическим ожиданием (Мх) случайной величины Х называется такое её значение, вокруг которого группируются результаты отдельных наблюдений; при нормальном распределении математическому ожиданию соответствует наибольшая плотность вероятности.

Для непрерывной случайной величины

(2)

Для дискретной случайной величины

, (3)

где р_i - вероятность значения величины Х_i.

Следует отметить, что для случайных погрешностей _сл математическое ожидание (среднее значение) равно нулю, и дифференциальная функция закона распределения принимает вид

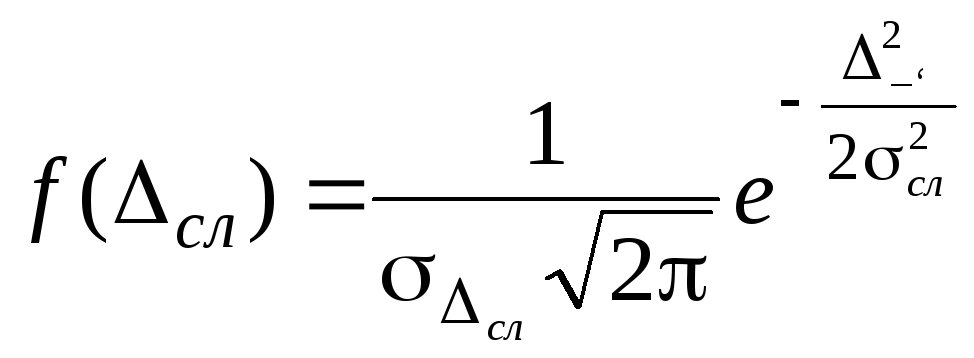(4)

Статистической оценкой математического ожидания для ряда однородных результатов является среднее арифметическое:

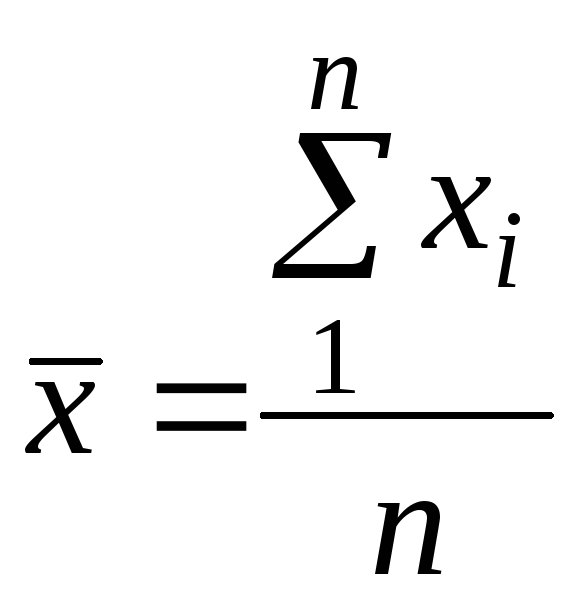(5)

Среднее квадратическое отклонение _x случайной величины представляет собой меру рассеивания значений случайной величины относительно её математического ожидания.

,

где D_x - дисперсия случайной величины:

Чем больше дисперсия (или среднее квадратическое отклонение), тем значительнее рассеивание. На рис. 1 Dx₂  Dx₁

Статистической оценкой СКО является так называемое стандартное отклонение:

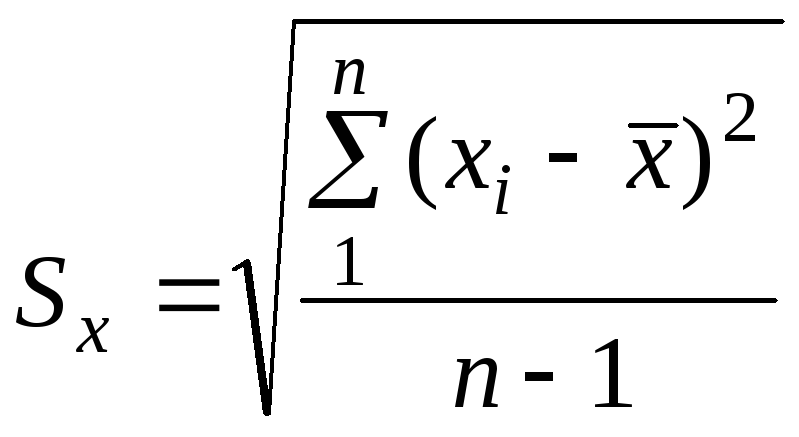, (6)

где n - число наблюдений (измерений).

Вероятность попадания случайной величины в интервал (х₁, х₂) равна:

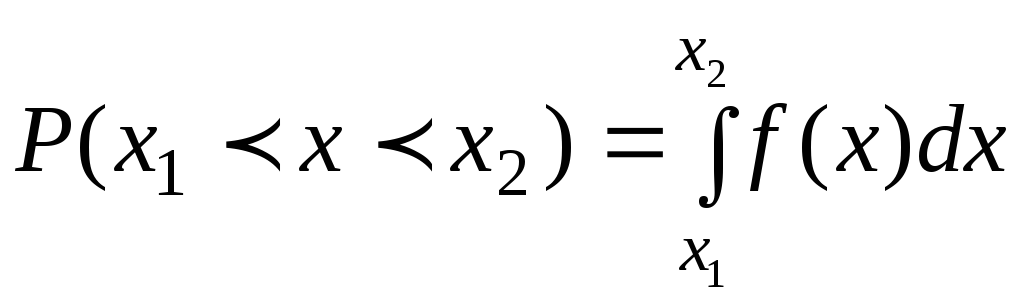(7)

что соответствует площади под кривой распределения на этом участке (рис.1)

Интервал , который с заданной вероятностью Р покрывает истинное значение случайной величины, называется доверительным интервалом, а вероятность Р - доверительной вероятностью. Отношение доверительного интервала к среднему квадратическому отклонению - это относительный доверительный интервал:

(8)

При достаточно большом число наблюдений (измерений) вычисленное стандартное отклонение близко к действительному значению среднего квадратического отклонения. Если при этом установлено, что закон распределения вероятности результатов измерения - нормальный, то для нахождения относительного доверительного интервала по доверительной вероятности (и наоборот, доверительной вероятности по относительному доверительному интервалу) используются математические таблицы специальной функции Лапласа. Аргументом функции Лапласа является относительный доверительный интервал, рассчитываемый по формуле:

(9)

Однако действия с функцией Лапласа оказываются тем менее надежными, чем меньше число наблюдений. В подобных случаях следует определять доверительную вероятность или доверительный интервал по таблицам распределения Стьюдента, в зависимости от числа набдюдений.

2.2. Обработка результатов многократных измерений

Многократные измерения одной и той же величины постоянного размера производится при повышенных требованиях к точности измерений. Результат многократных измерений описывается выражением:

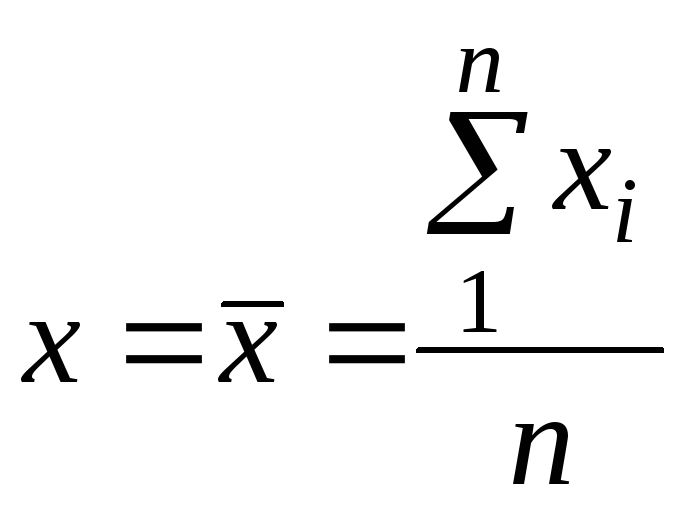(10)

Как и результат однократного измерения, он является случайным значением измеряемой величины, но его дисперсия в n раз меньше дисперсии результата однократного измерения:

, соответственно (11)

То есть точность определения значения измеряемой величины повышается в раз.

Результат многократных измерений записывается в форме доверительного интервала

(12)

где величина t находится в зависимости от заданной доверительной вероятности.

При проведении многократных измерений некоторые результаты могут содержать грубые погрешности, то есть погрешности, явно превышающие по своему значению погрешности, оправданные условиями проведения эксперимента (измерения). Очевидно, что наиболее подозрительными являются минимальное и максимальное показания. Вопрос о том, содержит ли данный результат грубую погрешность, решается общими методами проверки статистических гипотез.

Проверяемая гипотеза состоит в утверждении, что результат х_i не содержит грубой погрешности. Для проверки этой гипотезы используют распределения следующих величин:

(13)

(14)

Эти функции совпадают между собой, и для нормального распределения результатов измерения они протабулированы. По таблице 1 (Приложение стр. 22) по заданной доверительной вероятности Р и количестве измерений в серии n находят табличное (предельно допустимое) значение _т; его сравнивают с расчетным значением _р. Если выполняется условие _р  _т , то гипотеза об отсутствии грубой погрешности принимается с вероятностью Р.

Иногда грубые погрешности исключаются с помощью правила «трех сигм». Если известно, что закон распределения - нормальный, и его числовые характеристики (их оценки) равны Мх и _х, то с доверительной вероятностью 0,9973 грубыми промахами являются те результаты измерения, которые выходят за границы интервала Мх _х.

После того, как грубые погрешности (промахи) исключены из результатов измерения, необходимо снова определить оценки числовых характеристик и убедиться в отсутствии грубых погрешностей.

2.3. Равноточные и неравноточные измерения. Серии измерений.

Если изменением измеряемой величины во времени можно пренебречь, то все значения отсчета при многократных измерениях получает один оператор с помощью одного и того же средства измерений. При этом все значения отсчета будут распределены с одинаковой дисперсией; такие значения отсчета называются равноточными (равнорассеянными).

Если за время измерения может произойти существенное изменение измеряемой величины, то последнюю измеряют несколькими средствами измерений, каждое из которых дает одно из независимых значений отсчета. Так как средства измерений могут отличаться по точности, то случайные значения отсчета (результаты однократных измерений) могут иметь разную дисперсию; такие значения отсчета называются неравноточными (неравнорассеянными).

Часто измерительная процедура бывает организована таким образом, что с помощью каждого средства измерений получают ряд значений отсчета - серию измерений. При этом могут получаться как однородные, так и неоднородные серии.

Однородными сериями измерений называются такие, у которых вероятности результатов измерений подчиняются одному закону. На практике однородными считают такие серии измерений, у которых числовые характеристики законов распределения вероятности (ЗРВ) и отличаются случайным образом. Если хотя бы одна из этих числовых характеристик отличается от характеристик других серий неслучайно, то эти серии считаются неоднородными.

При неслучайном различии средних результаты серий измерений не подлежат совместной обработке, так как результаты измерений не сходятся.

При неслучайном различии дисперсий серии измерений являются неравноточными (неравнорассеянными).

Результаты равноточных и неравноточных серий измерений подлежат совместной обработке, но по различным методикам. Поэтому перед тем, как приступить к обработке результатов нескольких серий измерений, необходимо произвести проверку их однородности. Для этого проверяют равенство их средних арифметических и дисперсий.

Средние арифметические и двух серий измерений считаются равными, если их разность равна нулю:

Однако точно это равенство не выполняется из-за случайного характера величин и , поэтому средние считаются одинаковыми, если их разность меньше погрешности, с которой эту разность можно определить:

, (15)

где t - относительная ширина доверительного интервала,

- стандартное отклонение разности средних

Относительная ширина доверительного интервала (t) выбирается из распределения Стьюдента по таблице 2 (Приложение, стр. 23) в зависимости от заданной доверительной вероятности и от числа степеней свободы k. Для случая, когда одним и тем же прибором производят m серий измерений, число степеней свободы определяется по формуле

k = N – m,

где N –суммарное число измерений во всех сериях.

Поскольку при выполнении лабораторной работы осуществляется сравнение двух серий измерений, то m = 2

Стандартное отклонение разности средних () определяется по формуле:

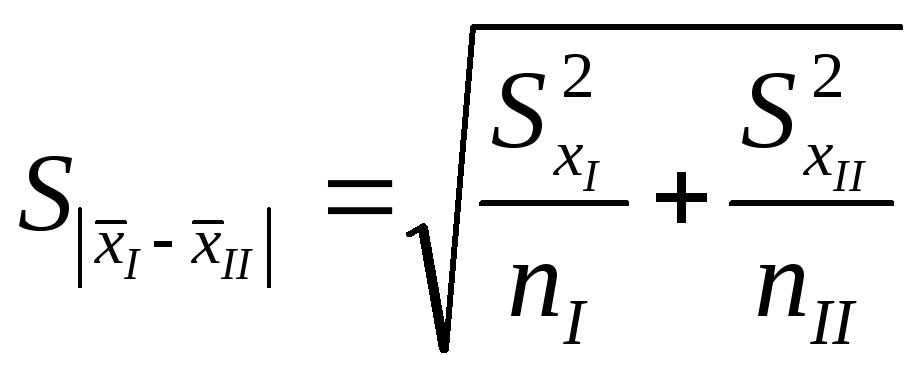, (16)

где n_I и n_II - число измерений в сериях I и II соответственно.

Если число серий больше двух, то необходимо провести попарное сравнение всех средних.

Что касается дисперсий, то уместнее говорить не об их равенстве, а об однородности, то есть о случайном (незначимом) различии. Как указывалось ранее, проверка неоднородности дисперсий позволяет определить методику дальнейшей обработки результатов измерений. Если дисперсии однородны, то обработка результатов ведется по схеме равноточных серий измерений, если же дисперсии неоднородны, то обработка результатов ведется по схеме неравноточных серий измерений.

Чаще всего для проверки однородности дисперсий используют критерий Фишера.

Критерий Фишера определяется по формуле:

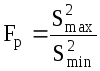, (17)

где F_р - расчетное значение критерия Фишера,

- наибольшая и наименьшая дисперсии из всех серий.

Если выполняется условие

, (18)

то дисперсии - однородны. Следовательно, остальные дисперсии однородны тем более.

Критическое (табличное) значение F-критерия F_т выбирается по таблице 3 (Приложение, стр. 24) в зависимости от доверительной вероятности Р и числа степеней свободы k₁ = n₁ - 1, k₂ = n₂ – 1, где k₁ и k₂ - числа степеней свободы для наибольшей и наименьшей дисперсий соответственно.

2.4. Обработка результатов нескольких серий измерений.

Если на основании проверок средних значений и дисперсий установлено, что серии измерений - однородные, то их можно объединить в единый массив и обрабатывать как результаты многократных равноточных измерений (п.2).

Если серии измерений признаны неравноточными, то каждую группу результатов наблюдений, относящихся к одинаковым условиям (каждую серию), необходимо оценить с точки зрения степени доверия, определить их «вес» в общей совокупности всех результатов, подлежащих обработке, для получения значения измеряемой величины, наиболее близкого к истинному.

Понятие «вес» отражает степень доверия к результату измерения. Чем больше степень доверия к результату, тем больше его вес, тем больше число, выражающее этот вес.

Весовые коэффициенты g_j оценивают вклад каждой серии в общий результат измерения. К ним предъявляются следующие требования:

1) ; m - число серий измерений

2) коэффициенты обратно пропорциональны дисперсиям

Значение весового коэффициента g_j можно определить по следующей формуле:

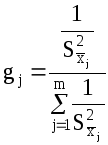(19)

Среднее значение для таких серий измерений определится как среднее взвешенное:

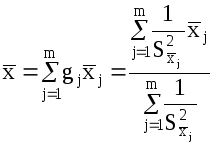(20)

Оценка дисперсии рассчитывается по формуле:

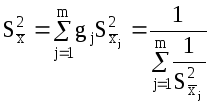(21)

Окончательный результат записывается в принятой форме доверительного интервала согласно выражению (12).

2.5. Описание измерительного прибора, используемого в работе.

Рычажные скобы предназначены для точных измерений наружных линейных размеров. Измерение осуществляется путем сравнения размера контролируемого изделия с размером концевой меры длины, по которой предварительно настраивается прибор.

Рычажная скоба (рис.2) снабжена тремя контактами - двумя неподвижными 1 и 2 и одним подвижным 3. Подвижный контакт, перемещаясь внутри корпуса 7, надавливает на короткое плечо рычага 4. Длинное плечо этого рычага заканчивается зубчатым сектором; сектор сцепляется с шестеренкой 5, сидящей на одной оси со стрелкой.

Таким образом, перемещение подвижного контакта вызывает поворот стрелки относительно шкалы. Спиральная пружина 6 служит для создания измерительного усилия между контактом и измеряемой деталью.

Для того, чтобы облегчить установку скобы относительно объекта и уменьшить износ контактов, предусмотрено специальное устройство - арретир, состоящее из штифта 8 и второго рычага 9. При нажатии на штифт 8 рычаг поворачивается по часовой стрелке, надавливает на контакт 3 и отводит его от поверхности измеряемого объекта.

Настройку скобы на номинальное значение измеряемого размера осуществляют перемещением контакта 1. Для этого следует отвинтить (не снимая) колпачок 10 и вращать накатную гайку 11. Сменный контакт 2 служит для облегчения установки прибора по диаметру измеряемых изделий цилиндрической формы.

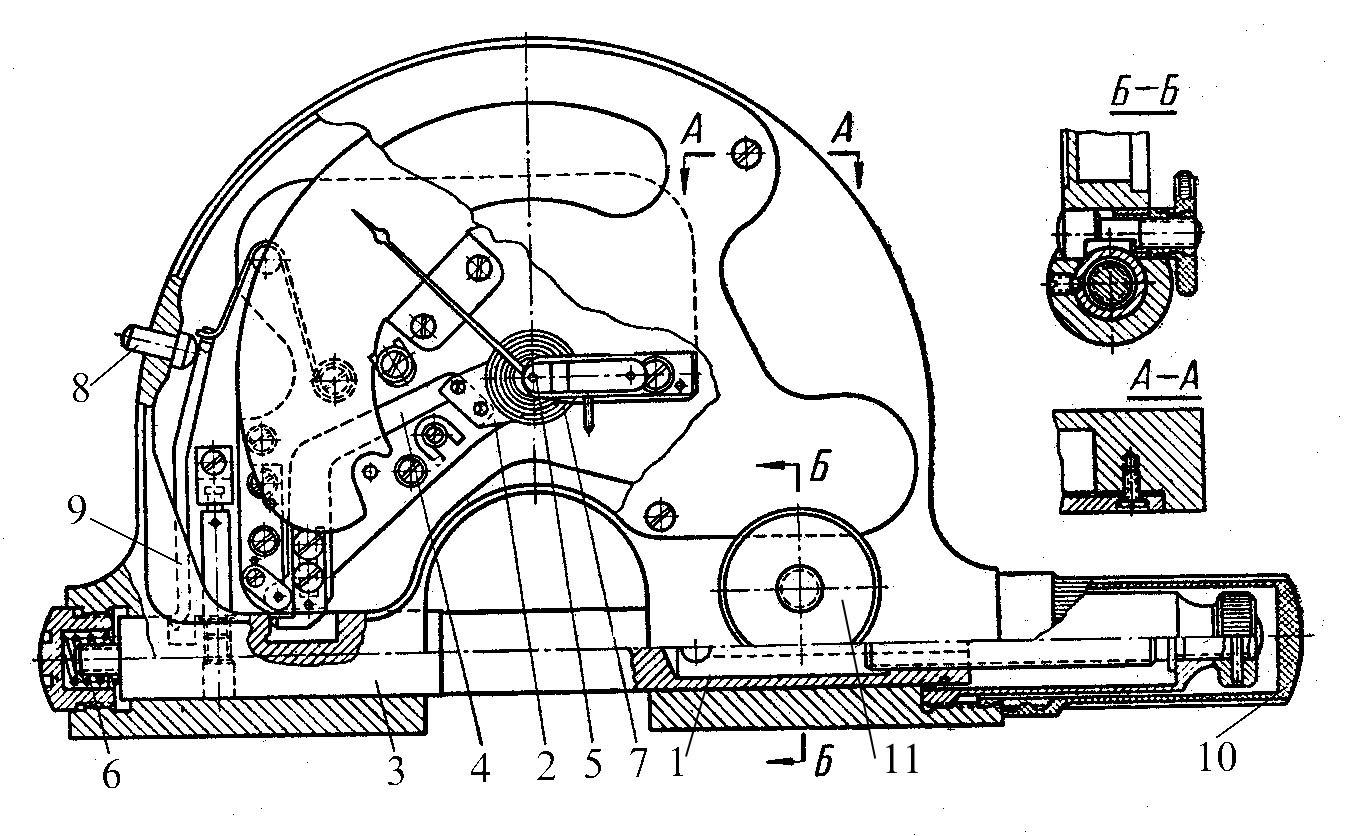
Рисунок 2 – Схема рычажной скобы