Работа № 8 изучение эффекта холла в полупроводниках Краткая теория

В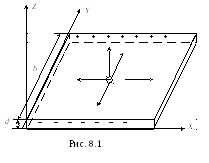1879 г. американский физик Эдвин Герберт Холл (E.H. Hall, 1855-1938) обнаружил, что при помещении тонкой пластины с токомI в магнитное поле, перпендикулярное плоскости пластины, в ней возникает поперечная разность потенциалов, которую назвали напряжением Холла. Проведённые измерения показали, что холловское напряжение U прямо пропорционально индукции В магнитного поля и силе тока I и обратно пропорционально толщине d пластины:

,

(8.1)

где R – коэффициент пропорциональности (коэффициент Холла), его величина и знак зависят от заряда и концентрации носителей тока.

Рассмотрим элементарную теорию эффекта Холла. Пусть носителями тока являются электроны (например, в металлах и в полупроводниках n-типа). При протекании в образце тока плотностью j электроны имеют скорость направленного движения  (скорость дрейфа), направленную против направления тока (рис. 8.1). Если проводник с током помещен в магнитное поле, то на электроны действует сила Лоренца:

FЛ = ,

(8.2)

направленная перпендикулярно их скорости (см. рис. 8.1). Электроны будут отклоняться к одной из граней, оставляя на противоположной стороне пластины не скомпенсированный положительный заряд. В результате вдоль оси Y появится поперечное электрическое поле, действующее на электрон с силой

,

(8.3)

которая направлена противоположно силе Лоренца. Накопление зарядов будет продолжаться до тех пор, пока возникшее электрическое поле не скомпенсирует отклоняющее действие магнитного поля. При равенстве модулей сил

eE = eB

(8.4)

установится стационарное состояние, то есть постоянное поперечное электрическое поле Холла, напряжённость которого

E = B,

(8.5)

если магнитное поле перпендикулярно скорости дрейфа электронов.

Полагая поле Холла однородным, найдём разность потенциалов между противоположными гранями пластины (напряжение Холла)

(8.6)

где b – ширина пластины, или размер образца вдоль направления поля Холла.

Скорость  электронов можно выразить через силу тока:

; j = en;  ,

(8.7)

где n – концентрация носителей тока в пластине.

Подставив скорость (8.7) в равенство (8.6), получим напряжение Холла

.

(8.8)

Сравнивая выражения (8.1) и (8.8), получаем коэффициент Холла

.

(8.9)

Из этой формулы следует, что знак коэффициента Холла определяется знаком заряда носителей тока. Для металлов и полупроводников n-типа R < 0, а для полупроводников с дырочной проводимостью (р-типа) R > 0.

Способ определения коэффициента Холла

Напряжение Холла, согласно формуле (8.1), линейно зависит от магнитной индукции В и от тока I, протекающего в датчике. Установка позволяет получить зависимость U(В) и по угловому коэффициенту экспериментальной прямой определить постоянную Холла R.

Величина индукции В магнитного поля в зазоре электромагнита зависит от силы тока I_ЭМ в его обмотке, числа витков N и от величины зазора h:

.

(8.10)

Для корректного измерения напряжения Холла нужно учесть, что при проведении эксперимента в пластинке имеется не только поле ХоллаЕ_у (рис. 8.2)., но и электрическое поле Е_х, обеспечивающее протекание тока I в датчике. Это продольное поле создаёт разность потенциалов между точками, расположенными на разных расстояниях от начала датчика. Если контакты, с которых снимается напряжение Холла, смещены относительно эквипотенциальной поверхности, которая перпендикулярна полю Е_х, то и без магнитного поля между ними будет разность потенциалов

,

(8.11)

где х – расстояние между контактами по координате х (рис. 8.2).

Измеряемая разность потенциалов _А – _В будет равна алгебраической сумме напряжений U + и может быть как меньше (при разных знаках), так и больше напряжения Холла. Для исключения этой систематической ошибки нужно измерять поперечную разность потенциалов U₁ = U + и U₂ = U – при двух противоположных направлениях магнитного поля и затем находить среднее значение

.(8.12)Практически для реализации этого приёма изменяют направление тока в обмотке электромагнита. Как следует из рис. 8.2, при этом изменяется и полярность напряжения Холла. Для получения правильного результата напряжения U₁ и U₂ в формуле (8.12) нужно брать без учёта знака.