Discrete math with computers_3

Definition 43. Let A be a set and let R :: A × A be a relation defined over A. The nth power of R, denoted Rn, is defined as follows:

R0 = {(a, a) | a A}

Rn+1 = Rn; R

Example 55. Using the formal definition, we calculate R4, where

R = {(2, 3), (3, 2), (3, 3)}.

R0 is just the identity (equality) relation, which contains a reflexive loop for every node. By the definition, R1 = R0; R = R, because the identity relation composed with R just gives R. The first nontrivial calculation is to find R2 = R1; R = R; R. We have to take each pair (a, b) in R, and see whether there is a pair (b, c); if so, we need to put the pair (a, c) into R2. The result of this calculation is R2 = {(2, 2), (2, 3), (3, 2), (3, 3)}.

Now we have to calculate R3 = R2; R. We compose

{(2, 2), (2, 3), (3, 2), (3, 3)}

with

{(2, 3), (3, 2), (3, 3)},

which yields

{(2, 2), (2, 3), (3, 2), (3, 3)}.

At this point, it’s helpful to notice that R3 = R2. In other words, composing R2 with R just gives R2 back, and we can do this any number of times. This means that any further powers will be the same as R2—so we have found R4 without needing to do lots of calculations with ordered pairs.

Relational composition is associative. This causes the powers of a relation to follow algebraic laws that are similar to the corresponding laws for powers on numbers. For example, R(a+b) = Ra; Rb.

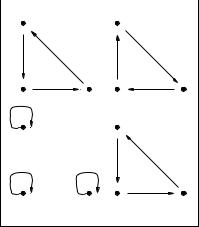
A relation whose domain is {x0, . . . , xn−1} is cyclic if it contains a cycle of ordered pairs of the form (x0, x1), (x1, x2), (x2, x3), (x3, x4), . . . , (xn−1, x0). That is, the relation is cyclic if there is a cycle comprising all the elements of its domain.

Consider what happens to a cyclic relation as we calculate its powers. The relation is defined as

R = {(a, b), (b, c), (c, a)}.

The first power R1 is just R. The second power R2 is calculated by working out the ordered pairs in R; R; the result is

R2 = {(a, b), (b, c), (c, a)}; {(a, b), (b, c), (c, a)}

= {(a, c), (b, a), (c, b)}.

a

Figure 10.14: Four Powers of a Cyclic Relation

This contains only paths between the start and end points of all the paths of length two in the original relation. Now the third power is

This result contains only arcs connecting the origin and destination points of paths of length three in the original relation. What will happen next?

Just what we might have expected: each of these arcs represents a path of length 4, so we have started round the cycle again. What can we now say about the powers of this relation? They repeat in a cycle. R4 = R1, R5 = R2 and in general Rn+3 = Rn (Figure 10.14).

The software tools file defines the following function, which takes a set and returns the equality relation on that set.

equalityRelation ::

(Eq a, Show a) => Set a -> Relation a

There is also a function that calculates the power of a relation:

relationalPower ::

(Eq a, Show a) => Digraph a -> Int -> Relation a

Exercise 15. Work out the values of these expressions, and then evaluate them using the computer:

equalityRelation [1,2,3] equalityRelation ([]::[Int])

Exercise 16. Calculate the following relational powers by hand, and then evaluate them using the computer.

relationalPower ([1,2,3,4],[(1,2),(2,3),(3,4)]) 1 relationalPower ([1,2,3,4],[(1,2),(2,3),(3,4)]) 2 relationalPower ([1,2,3,4],[(1,2),(2,3),(3,4)]) 3 relationalPower ([1,2,3,4],[(1,2),(2,3),(3,4)]) 4

Exercise 17. Why do we not need to check the ordered pairs in R while calculating R0; R ?

Exercise 18. Why can we stop calculating powers after finding that two successive powers are the same relation?

Exercise 19. What is R4 where R is {(2, 2), (4, 4)}?

Exercise 20. What is the relationship between adding new ordered pairs to make a relation transitive and taking the power of a relation?

Exercise 21. Suppose a set A contains n elements. How many possible relations with type R :: A × A are there?

Exercise 22. Given the relation {(a, b), (b, c), (c, d), (d, e)}, how many times would we have to compose this relation with itself before the empty relation is produced?

Exercise 23. Given the set A = {1, 2, 3} and the relation R :: A × A where

R= {(3, 1), (1, 2), (2, 3)}, what is the value of R2? R3?

10.7Closure Properties of Relations

In computing applications, we normally want to keep the specification of a relation as small and readable as possible, so that it can be defined and maintained accurately. On the other hand, some computations may require the relation to have some special properties (for example, symmetric or transitive). These special properties would require adding a large number of ordered pairs to the relation, making it harder to maintain. There is a standard technique used in such situations—we define two relations:

1.A basic relation, containing just the essential information, is specified;

2.A larger relation is derived from the basic one by adding the ordered pairs required to give it the special properties that are needed.

When circumstances change, only the basic relation is edited by hand. The derived relation is recalculated using a computer.

Example 56. An airline keeps a set of all the flights they o er. This is represented by a relation Flight, where (a, b) Flight if the airline has a direct flight from a to b. However, when a customer asks a question like ‘Do you fly from Glasgow to Seattle?’, the airline needs a transitive relation: if (Glasgow, New York) Flight and also (New York, Seattle) Flight, the answer should be yes. Thus the airline’s flight-planning sta define the basic relation Flight, but the sales sta work with a derived relation that is similar to Flight, but which is transitive.

A relation derived in this way is called the closure of the basic relation:

Definition 44. The closure of a relation R with respect to a given property is the smallest possible relation that contains R and has that property.

Closure is suitable for adding properties that require the presence of certain ordered pairs. For example, you can take the symmetric closure of a relation by checking every existing pair (x, y), and adding the pair (y, x) if it isn’t already present. However, closure is not suitable for properties that require the absence of certain ordered pairs. For example, the relation R = {(1, 1), (1, 2), (2, 3)} does not have an irreflexive closure, as that would need to contain (1, 1) (because the closure must contain the basic relation), yet it must not contain (1, 1) (in order to be irreflexive).

You can give a relation a property such as reflexivity, or transitivity, by creating its reflexive or transitive closure. Notice, however, that the new relation may no longer have all of the properties of the original relation. For example, suppose that a relation is irreflexive, as in {(1, 2), (2, 1)}. The smallest possible transitive relation containing this one also has the arcs (1,1) and (2,2), which means that it is no longer irreflexive.

10.7.1Reflexive Closure

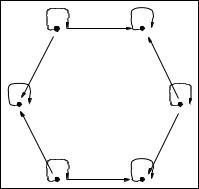
The reflexive closure of a relation contains all of the arcs in the relation together with an arc from each node to itself. For example, consider the set

{Red, Orange, Yellow, Green, Blue, Violet}.

The relation ContainsPrimaryColour is given in Figure 10.15 by the solid arcs. It is not reflexive, because the colours that are not primary colours do not contain reflexive arcs. However, the relation ContainsColour is reflexive (given by all the arcs in Figure 10.15), and is in fact the reflexive closure of ContainsPrimaryColour.

The formal definition that follows defines the reflexive closure of a relation R as the smallest reflexive relation containing the arcs of R.

Figure 10.15: The ContainsColour and ContainsPrimaryColour Relations

Definition 45. Let A be a set, and let R :: A × A be a binary relation over A. The reflexive closure of R is the relation R such that R is reflexive, R is a superset of R, and for any reflexive relation R , if R is a superset of R, then R is a superset of R . The notation r(R) denotes the reflexive closure of R.

Example 57. The reflexive closure of the relation {(1, 2), (2, 3)} over the set {1, 2, 3} is {(1, 1), (2, 2), (3, 3), (1, 2), (2, 3)}.

Example 58. The relation {(1, 1), (1, 2), (3, 3), (2, 3)} is not the reflexive closure of {(1, 2), (2, 3)}, because it is missing the reflexive arc (2, 2).

The following theorem provides a straightforward method for calculating the reflexive closure of a relation:

Theorem 73. Let A be a set, let E be the equality relation on A, and let R be a binary relation defined over A. Then r(R) = R E.

All we have to do to calculate the reflexive closure R :: A × A is to add self-loops (x, x) for all of the nodes x in the set A over which the relation R is defined.

The software tools file provides the following function, which automates the calculation of reflexive closures:

reflexiveClosure ::

(Eq a, Show a) => Digraph a -> Digraph a

Exercise 24. Work out the following reflexive closures by hand, and then check your results using the computer:

reflexiveClosure ([1,2,3],[(1,2),(2,3)]) reflexiveClosure ([1,2],[(1,2),(2,1)])

Exercise 25. What is the reflexive closure of the relation R; R, where R is defined as {(1, 2), (2, 1)}?

Figure 10.16: The Symmetric Closure of {(1, 2)}

symmetricClosure ::

(Eq a, Show a) => Digraph a -> Digraph a

Exercise 26. Work out the following symmetric closures by hand, and then calculate them using the computer window:

symmetricClosure ([1,2],[(1,1),(1,2)]) symmetricClosure ([1,2,3],[(1,2),(2,3)])

Exercise 27. What is the symmetric reflexive closure of the relation

{(a, b), (b, c)}?

Hint: take the reflexive closure first, followed by the symmetric closure of the result.

Exercise 28. Find the reflexive symmetric closure of the relation {(a, c)}.

10.7.3Transitive Closure

The transitive closure is one of the most important operations on relations. You can define a relation that describes one step; the transitive closure of the relation then describes the e ect of taking n steps, for any n.

Example 61. Suppose that Flight is the relation where (a, b) Flight if there is a direct flight from city a to city b. Then the transitive closure of Flight is the relation consisting of pairs (a, b) where b is reachable by air from a.

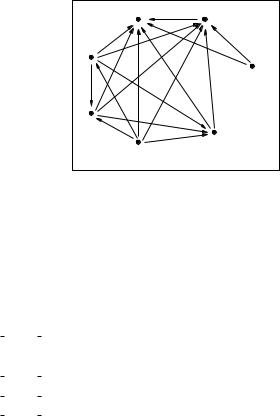
Consider now how to calculate the transitive closure of a relation. As an example, suppose that you need to define the IsDescendantOf relation in a database of people. The database contains records for Zoe, Bruce, Gina, Annabel, Dirk, Kay, and Don. We start with the IsChildOf relation, defined as follows:

{(Zoe, Bruce), (Gina, Zoe),

(Bruce, Annabel ), (Dirk , Kay),

(Kay, Don), (Annabel , Kay)}

Observe that the relation IsDescendantOf should have all these arcs, and many more. For example, Gina is a descendant of Bruce.

Figure 10.17: The IsDescendantOf Relation

How many more arcs need to be added? There should be an arc between the origin and destination points of each path of length 2 or more in the IsChildOf relation. In other words, we need the transitive closure of IsChildOf.

The powers of the IsChildOf relation are as follows:

The IsDescendantOf relation contains the union of all of these powers (Figure 10.17):

IsDescendantOf =

{(Zoe, Bruce), (Gina, Zoe), (Bruce, Annabel), (Dirk, Kay),

(Kay, Don), (Annabel, Kay), (Zoe, Annabel), (Gina, Bruce),

(Bruce, Kay), (Dirk, Don), (Annabel, Don), (Zoe, Kay),

(Gina, Annabel), (Bruce, Don), (Zoe, Don), (Gina, Kay),

(Gina, Don)}

The calculations we have just gone through suggest an algorithm for calculating the transitive closure of any relation: calculate all the powers R1, R2, and so on, up to Rn, and take their union. There are n nodes in the digraph, so the longest possible path (ignoring cycles) must be no more than n−1 elements long. The transitive closure must provide a short cut for each path, which is why we must include a power of the relation for each possible path length. This leads also to a way to define the transitive closure formally:

Definition 48. Let A be a set of n elements, and let R :: A × A be a binary relation over A. The transitive closure of R is defined as

n

t(R) = Ri.

i=1

For example, if a set A has four elements, then the transitive closure of a relation R :: A × A would be

R1 R2 R3 R4.

The IsDescendantOf relation is the union of as many powers of the IsChildOf relation as there are people in the IsChildOf relation’s domain.

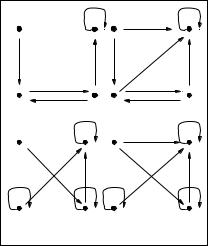
Example 62. Using the definition, we calculate the transitive closure of R = {(1, 2), (2, 3), (3, 2), (3, 4), (4, 4)}. There are four elements in the set over which the relation is defined (we haven’t specified otherwise), so we shall need to calculate the union of the relations R, R2, R3, and R4 (Figure 10.18). First, we calculate:

The union of all of these relations is the transitive closure of R:

{(1, 2), (1, 3), (1, 4), (2, 2), (2, 3), (2, 4), (3, 2), (3, 3), (3, 4), (4, 4)}

The following function calculates the transitive closure of a relation, using the definition:

transitiveClosure ::

(Eq a, Show a) => Digraph a -> Digraph a

Exercise 29. Work out the following transitive closures by hand, and then evaluate them using the computer:

transitiveClosure ([1,2,3],[(1,2),(2,3)]) transitiveClosure ([1,2,3],[(1,2),(2,1)])

Exercise 30. Given a digraph ({1, 2, 3, 4}, {(1, 2)}), what can we do to speed up the transitive closure algorithm, which requires that we take as many powers of this relation as there are nodes in the digraph?

Exercise 31. Find the transitive symmetric closure and the symmetric transitive closure of the following relations:

(a){(a, b), (a, c)}

(b){(a, b)}

(c){(1, 1), (1, 2), (1, 3), (2, 3)}

(d){(1, 2), (2, 1), (1, 3)}

Figure 10.18: The Powers of {(1, 2), (2, 3), (3, 2), (3, 4), (4, 4)}

10.8Order Relations

An order relation specifies an ordering that can be used to create a sequence from the elements of its domain. Order relations are extremely important in computing, because data values often need to be placed in a well-defined sequence for processing. The standard mathematical relations less-than (<) and less-than-or-equal (≤) are examples of order relations, but there are many more.

One of the most fundamental properties of an order relation is transitivity: if a precedes b in the ordering, and b precedes c, then we surely want a also to precede c. However, some of the other properties of relations may be present or absent, so there are several di erent kinds of order relation. We will examine these in turn, starting with partial orders.

10.8.1Partial Order

A partial order puts at least some of the elements in its domain into sequence, but not necessarily all of them. There could also be several sequences within a partial order, without any ordering between elements belonging to di erent subsequences.

Example 63. Suppose that a database of people contains records that specify the breed of dog owned—for those people who have a dog. The records of dog owners could be ordered alphabetically using the breed name, producing a sequence of dog owners. However, this ordering would not include the people