Discrete math with computers_3

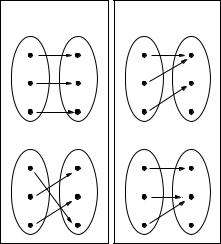
Figure 11.9: Two Injective Functions and Two That Are Not Injective

Definition 72. The function f :: A → B is injective if

a, a A. a = a → f a = f a

Example 121. Let A = {1, 2} and B = {3, 4, 5}. Define f :: A → B as {(1, 3), (2, 5)}. Then f is injective, because 3 appears in only one ordered pair, (1, 3), and 5 appears in only one ordered pair, (2, 5).

Example 122. Let A = {1, 2, 3} and B = {4, 5}. Define g :: A → B as {(1, 4), (2, 5), (3, 5)}. Then g is not injective because it contains the ordered pairs (2, 5) and (3, 5), which have di erent argument values but the same result value.

Example 123. Figure 11.9 shows four functions, two of which are injective.

Example 124. The following Haskell functions are injective:

(/\) True :: Bool -> Bool increment :: Int -> Int id :: a -> a

times_two :: Int -> Int

Example 125. The following Haskell functions are not injective. The length function is not injective, because it will map both [1,2,3] and [3,2,1] to the same number, 3. There are infinitely many other examples that would su ce to show that length is not injective, but you only have to give one. The function take n is not injective because it will map both [a1, a2, . . . , an, x] and [a1, a2, . . . , an, y] to the same result [a1, a2, . . . , an], even if x = y.

length :: [a] -> Int take n :: [a] -> [a]

The software tools file defines the following function, which determines whether a function (specified by its graph) is injective. The first argument is the function’s domain, represented as a set; the second argument is its result type, also represented as a set; and the third argument is its graph.

isInjective

:: (Eq a, Show a, Eq b, Show b)

=> Set a -> Set b -> Set (a, FunVals b) -> Bool

Example 126. Let A = {1, 2, 3} and B = {4, 5, 6}. Define three functions as follows:

We can use the software tools to explore the properties of various compositions of these functions. First we need to represent the function graphs in Haskell:

fun_domain = [1,2,3] fun_codomain = [4,5,6]

fun1 = [(1, Value 4), (2, Value 6), (3, Value 5)] fun2 = [(1, Value 4), (2, Value 4), (3, Value 5)] fun3 = [(1, Value 4), (2, Undefined), (3, Value 5)]

Now we can try various experiments:

isInjective fun_domain fun_codomain (functionalComposition fun1 fun2) isInjective fun_domain fun_codomain (functionalComposition fun1 fun3) isInjective fun_domain fun_codomain (functionalComposition fun2 fun3)

Exercise 12. Determine whether the functions in these examples are injective, and check your conclusions using the computer:

(a)isInjective [1,2,3] [2,4]

[(1,Value 2),(2,Value 4),(3,Value 2)]

(b)isInjective [1,2,3] [2,3,4]

[(1,Value 2),(2,Value 4),(3,Undefined)]

Exercise 13. Which of the following functions are injective?

(a)f :: A → B, where A = {1, 2}, B = {1, 2, 3} and f = {(1, 2), (2, 3)}.

(b)g :: C → D, where C = {1, 2, 3}, D = {1, 2} and g = {(1, 1), (2, 2)}.

Exercise 14. Suppose that f :: A → B and A has more elements than B. Can f be injective?

11.6.3The Pigeonhole Principle

The Pigeonhole Principle encapsulates a common sense form of reasoning about the relationship between two finite sets. It says that if A and B are finite sets, where |A| > |B| then no injection exists from A to B. In other words, since each element of the domain must be assigned a pigeonhole in the image, and the domain is bigger than the image, then there must be an element left over, because at most one pigeon fits in a pigeonhole. This principle is frequently used in set theory proofs, especially proofs of theorems about functions. There are a variety of ways in which to state the pigeonhole principle formally.

Theorem 78 (Pigeonhole Principle). Let A and B be finite sets, such that |A| > |B| and |A| > 1. Let f :: A → B. Then

a1, a2 A. (a1 = a2) (f a1 = f a2).

11.7Bijective Functions

Definition 73. A function is bijective if it is both surjective and injective. An alternative name for ‘bijective’ is one-to-one and onto. A bijective function is sometimes called a one-to-one correspondence.

Example 127. Figure 11.10 shows some bijective functions and some that are not bijective.

The domain and image of a bijective function must have the same number of elements. This is stated formally in the following theorem:

Theorem 79. Let f :: A → B be a bijective function. Then |domain f | = |image f |.

Proof. Suppose that the domain A is larger than the image B. Then f cannot be injective, by the Pigeonhole Principle. Now suppose that B is larger than A. Then not every element of B can be paired with an element of A: there are too many of them, so f cannot be surjective. Thus a function is bijective only when its domain and image are the same size.

A bijective function must have a domain and image that are the same size, and it must also be surjective and injective. As before, we assume that

Figure 11.10: Two Bijective Functions and Two That Are Not Bijective

these functions are finite. The following function, defined in the software tools file, takes a domain, codomain, and a function, and it determines whether the function is bijective.

isBijective

:: (Eq a, Show a, Eq b, Show b) => Set a -> Set b

-> Set (a,FunVals b) -> Bool

Exercise 15. Determine whether the following functions are bijective, and check your conclusions using the computer:

isBijective [1,2] [3,4] [(1,Value 3),(2,Value 4)] isBijective [1,2] [3,4] [(1,Value 3),(2,Value 3)]

11.7.1Permutations

Definition 74. A permutation is a bijective function f :: A → A; i.e., it must have the same domain and image.

Example 128. The identity function is a permutation.

The only thing a permutation function can do is to shu e its input; it cannot produce any results that do not appear in its input.

Example 129. Let A = {1, 2, 3} and let f :: A → A be defined by the graph {(1, 2), (2, 3), (3, 1)}. Then f is a permutation.

Example 130. Let X = [x1, x2, . . . , xn] be an array of values, and let Y = [y1, y2, . . . , yn] be the result of sorting X into ascending order. Define A = {1, 2, . . . , n} to be the set of indices of the arrays X and Y . We can define a function f :: A → A that takes the index of a data value in X and returns the location of that same data value in Y . Then f is a permutation.

Sometimes it is convenient to think of a permutation as a function that reorders the elements of a list; this is often simpler and more direct than defining a function on the indices. For example, it is natural to say that a sorting function has type [a] → [a]. Technically, the function f used in Example 130 is a permutation. The following definition provides a convenient way to represent a permutation as a function that reorders the elements of a list:

Definition 75. A list permutation function is a function f :: [a] → [a] that takes a list of values and rearranges them using a permutation g, such that

xs !! i = (f xs) !! (g i).

Example 131. The functions sort and reverse are list permutation functions.

If you rearrange a list of values and then rearrange them again, you simply end up with a new rearrangement of the original list, and that could be described directly as a permutation. This idea is stated formally as follows:

Theorem 80. Let f, g :: A → A be permutations. Then their composition f ◦ g is also a permutation.

The following function, defined in the software tools file, determines whether a function is a permutation. The first two arguments are the domain and result type, which must be finite sets with equality, and the third argument is the function graph.

isPermutation

:: (Eq a, Show a) => Set a -> Set a

-> Set (a,FunVals a) -> Bool

Exercise 16. Let A = {1, 2, 3} and f :: A → A, where

f = {(1, 3), (2, 1), (3, 2)}. Is f bijective? Is it a permutation?

Exercise 17. Determine whether the following functions are permutations, and check using the computer:

isPermutation [1,2,3] [1,2,3]

[(1,Value 2),(2, Value 3),(3, Undefined)] isPermutation

[1,2,3] [1,2,3]

[(1,Value 2),(2, Value 3),(3, Value 1)]

Exercise 18. Is f, defined below, a permutation?

f :: Integer -> Integer f x = x+1

Exercise 19. Suppose we know that the composition f ◦ g of the functions f and g is surjective. Show that f is surjective.

11.7.2Inverse Functions

A function f :: A → B takes an argument x :: A and gives the result (f x) :: B. The inverse of the function goes the opposite direction: given a result y :: B, it produces the argument x :: A, which would cause f to yield the result y.

Not all functions have an inverse. For example, if both (1, 5) and (2, 5) are in the graph of a function, then there is no unique argument that yields 5. Therefore the definition of inverse requires the function to be a bijection.

Definition 76. Let f :: A → B be a bijection. Then the inverse of f , denoted f −1, has type f −1 :: B → A, and its graph is

(y, x) | x, y. (x, y) f .

Example 132. Let A = {1, 2, 3}, B = {4, 5, 6} and let f :: A → A have the graph

{(1, 4), (2, 5), (3, 6)}. Then its inverse is f −1 = {(4, 1), (5, 2), (6, 3)}.

Example 133. The Haskell function decrement is the inverse of increment. Similarly, increment is the inverse of decrement.

increment, decrement :: Integer -> Integer increment x = x+1

decrement x = x-1

Exercise 20. Suppose that f :: A → A is a permutation. What can you say about f −1?

11.8Cardinality of Sets

One of the most fundamental properties of a set is its size, and this must be defined carefully because of the subtleties of infinite sets. Bijections are a crucial tool for reasoning about the sizes of sets.

A bijection is often called a one-to-one correspondence, which is a good description: if there is a bijection f :: A → B, then it is possible to associate each element of A with exactly one element of B, and vice versa. This is really what you are doing when you count a set of objects: you associate 1 with one of them, 2 with the second, and so on. When you have associated all the objects with a number, then the number n associated with the last one is the

number of objects. Thus the number of objects in S is n, if there is a bijection f :: {1, 2, . . . , n} → S. This idea is used formally to define the size of a set, which is called its cardinality:

Definition 77. A set S is finite if and only if there is a natural number n such that there is a bijection mapping the natural numbers {0, 1, . . . , n − 1} to S. The cardinality of S is n, and it is written as |S|.

In other words, if S is finite then it can be counted, and the result of the count is its cardinality (i.e., the number of elements it contains).

We would also like to define what it means to say that a set is infinite. It would be meaningless to say ‘a set is infinite if the number of elements is infinity’, because infinity is not a natural number. We need to find a more fundamental property that distinguishes infinite sets from finite ones.

A relevant observation is that we can make a one-to-one correspondence between the set N of natural numbers and the set E of even numbers, and yet there are natural numbers that are not even.

Now, we can calculate the ith element of the second row by applying f to the ith element of the first row, where f :: N → E is defined by f x = 2 × x. Furthermore, f is an injective function, and E is a proper subset of N . It would certainly be impossible to find an f with these properties for a finite set. This suggests a method for defining infinite sets:

Definition 78. A set A is infinite if there exists an injective function f :: A → B such that B is a proper subset of A.

We can use the properties of a function over a finite domain A and result type B to determine their relative cardinalities:

•If f is a surjection then |A| ≥ |B|.

•If f is an injection then |A| ≤ |B|.

•If f is a bijection then |A| = |B|.

Earlier we discussed counting the elements of a finite set, placing its elements in a one-to-one correspondence with the elements of {1, 2, . . . , n}. Even though there is no natural number n which is the size of an infinite set, we can use a similar idea to define what it means to say that two sets have the same size, even if they are infinite:

Definition 79. Two sets A and B have the same cardinality if there is a bijection f :: A → B.

Example 134. Let A = {1, 2, 3} and B = {cat, mouse, rabbit}. Define f ::

A → B as

f = {(1, cat), (2, mouse), (3, rabbit)}.

Now f is surjective and injective (you should check this), so it is a bijection. Hence the cardinality of B is

|B| = 3.

The previous example may look unduly complicated, but the point is that exactly the same technique can be used to investigate the sizes of infinite sets.

Example 135. We can place the set I of integers into one-to-one correspondence with the set N of natural numbers:

Now f is a bijection (you should check that it is), so I has the same cardinality as N .

We have already established that the cardinality of the set of even numbers is the same as the cardinality of N , so this is also the same as the cardinality of I. The size of the set of integers is the same as the size of the set of integers that are non-negative and even!

Definition 80. A set S is countable if and only if there is a bijection f :: N → S.

A set is countable if it has the same cardinality as the set of natural numbers. In daily life, we use the word counting to describe the process of enumerating a set with 1, 2, 3, . . . , so it is natural to call a set countable if it can be enumerated—even if the set is infinite.

Exercise 21. Explain why there cannot be a finite set that satisfies Definition 78.

Exercise 22. Suppose that your manager gave you the task of writing a program that determined whether an arbitrary set was finite or infinite. Would you accept it? Explain why or why not.

Exercise 23. Suppose that your manager asked you to write a program that decided whether a function was a bijection. How would you respond?

11.8.1The Rational Numbers Are Countable

It turns out that some infinite sets are countable and others are not, as we will see shortly. In computer science applications, it is particularly important to know whether an infinite set is countable, since a computer performs a sequence of operations that is countable. It is often possible for a computer to print out the elements of a countable set; it will never finish printing the entire set, but any specific element will eventually be printed. However, if a set is not countable, then the computer will not even be able to ensure that a given element will eventually be printed.

A rational number is a fraction of the form x/y, where x and y are integers. We can represent a ratio as a pair of integers, the first being the numerator and the second the denominator.

Now suppose that we want to enumerate all of these ratios: we need to put them into one-to-one correspondence with N . Our goal is to create a series of columns, each of which has an index n indicating its place in the series. A column gives all possible fractions with n as the numerator.

Every line in this sequence is finite, so it can be printed completely before the next line is started. Each time a line is printed, progress is made on all of the columns and a new one is added. Every ratio will eventually appear in the enumeration. Thus the set Q of rational numbers can be placed in one-to-one correspondence with N , and Q is countable.

Exercise 24. The software tools file contains a definition of a list named rationals, which uses the enumeration illustrated above. Try evaluating the following expressions with the computer:

take 3 rationals take 15 rationals

11.8.2The Real Numbers Are Uncountable

Obviously, if A B we cannot say that set B is larger than set A, since they might be equal. Surprisingly, even if we know that A is a proper subset of B, A B, we still cannot say that B has more elements: as the previous section demonstrated, it is possible that both are infinite but countable. For example, the set of even numbers is a proper subset of the set of natural numbers, yet both sets have the same cardinality!

It turns out that some infinite sets are not countable. Such a set is so much bigger than the set of natural numbers that there is no possible way to make a one-to-one correspondence between it and the naturals. The set of real numbers has this property. In this section we will explain why, and introduce a technique called diagonalisation which is useful for showing that one infinite set has a larger cardinality than another.

We will not give a formal definition of the set of real numbers, but will simply consider a real number to be a string of digits. Consider just the real numbers x such that 0 ≤ x < 1; these can be written in the form .d0d1d2d3 . . ..

There is no limit to the length of this string of digits.

Now, suppose that there is some clever way to place the set of real numbers into a one-to-one correspondence with the set of natural numbers (that is, suppose the set of reals is countable). Then we can make a table, where the ith row contains the ith real number xi, and it contains the list of digits comprising xi. Let us name the digits in that list di,0di,1di,2 . . .. Thus di,j means the jth digit in the decimal representation of the ith real number xi. Here, then, is the table which—it is alleged—contains a complete enumeration of the set of real numbers:

Now we are going to show that this list is incomplete by constructing a new real number y which is definitely not in the list. This number y also has a decimal representation, which we will call .dy0dy1dy2 . . .. Now we have to ensure that y is di erent from x0, and it is su cient to make the 0th digit of y (i.e., dy0) di erent from the corresponding digit of x0 (i.e., d00). We can do this by defining a function di erent :: Digit → Digit. There are many ways to define this function; here is one:

0, if x = 0

di erent x =

1, if x = 0

It doesn’t matter exactly how di erent is defined, as long as it returns a digit that is di erent from its argument.

We need to ensure that y is di erent from xi for every i N , not just for x0. This is straightforward: just make the ith digit of y di erent from the ith digit of xi:

dyi = di erent xii.

Now we have defined a new number y; it is real, since it is defined by a sequence of digits, and it is di erent from xi for any i. Furthermore, our construction of y did not depend on knowing how the enumeration of xi worked: for any alleged enumeration whatsoever of the real numbers, our construction will give a new real number that is not in that list. The conclusion, therefore,