2.6.1 Строго универсальное хеширование на основе ортогональных массивов

Определение 1.7 []. Пусть ,являются множествами изиэлементов, соответственно, иесть множество функций осуществляющих отображение.Ортогональным массивом называется массив элементов, со столбцами соответствующими элементам множестваи строками, определяемыми элементами множествав котором для любой выборки изэлементовизсуществует толькофункцийдля которых справедливо,.

Основная конструкция массивов определена следующим образом.

Пусть простое число,- целые числа,,. Зафиксируем сьюрективное- линейное отображение. Для каждогонабора, где,,, определим отображение:, вида

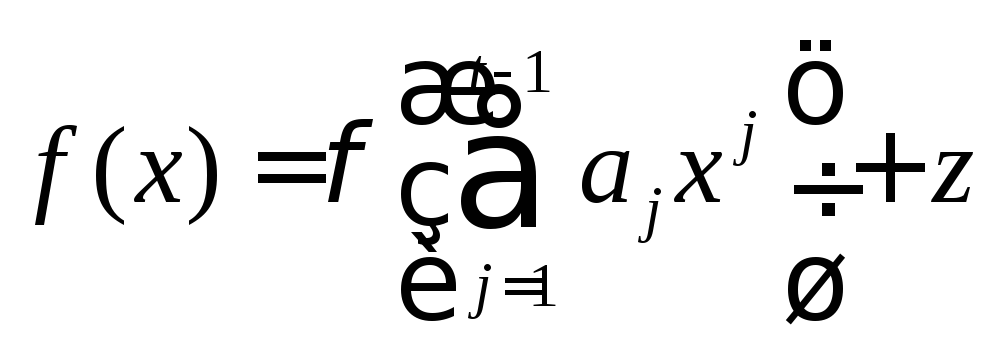. (1.12)

Массив, составленный из отображений вида (1.12) является ортогональным с параметрами .

Пусть простое число,,. Тогданазывается простым, каждая строка повторяется только (точно) один раз и определяется линейным отображениемс функцией, где.

Метод ортогональных массивов можно применить для построения строго универсальных хеш функций. Основной результат для отображения с функциейопределяется теоремой 2.1 [50].

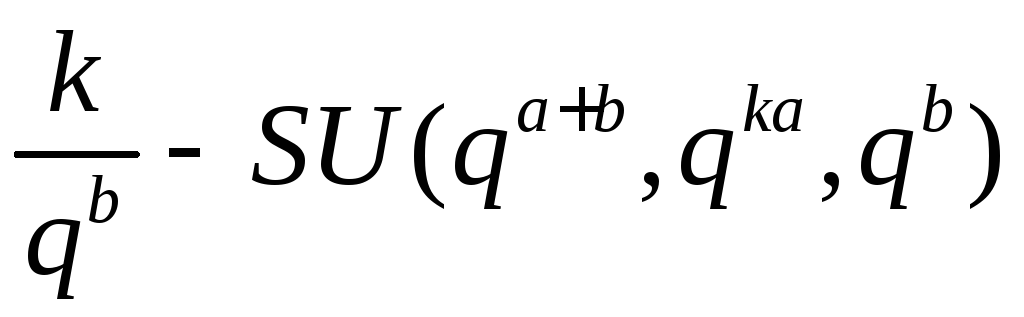Теорема 2.1. Пусть - простое число,,,целые числа,. Тогда существуетсемейство хеш-функций.

Замечание 2.6.

1. Если имеем строго универсальный класс хеш-функций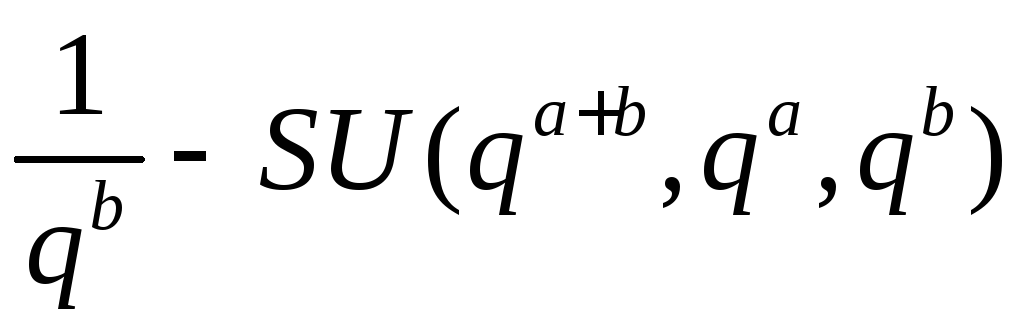. Размер ключевых данныхопределяется произведением пространства аутентификаторов и пространства сообщений, что уточняет ранее полученную границу из утверждения 1.5.

2. Для почти строго универсального хеширования снижаются требования к размеру ключевых данных, которое ограничивается размерами поля вычислений и.

2.6.2 Строго универсальное хеширование на основе почти независимых массивов

Почти независимые массивы (almost independent arrays) были рассмотрены Стинсоном [].Теория почти независимых массивов снимает ограничение на равновероятное распределение наборов хешей по столбцам массива. Почти независимые массивы являются обобщением ортогональных массивов.

Пусть -массив, содержащийстрок,столбцов и записи из набораэлементов. Длячастотапоявления значенияв столбцах массива удовлетворяет условию и для любых пар столбцов , частота появления в столбцах значений и удовлетворяет условию . Тогда-массив есть семейство хеш функций и .

Замечание 2.7.

1. Параметр определяется условной вероятностью появления любых записейдля различных столбцов, при равновероятном выборе строкии характеризует отклонение от равномерного распределения совместных вероятностей появления кодовых комбинаций впроизвольных столбцах случайно выбранной строкимассива.

2. Значение параметра зависимости определяет вероятность коллизии МАС кодов и в общем случае, как показано в [56], коллизионные свойстваt - кратных кодов аутентификации.

Практическое построение почти независимых массивов является проблематичным, так как нужны методы, которые позволяют формировать массивы хешей с заданными распределениями по столбцам. В этом отношении для построения строго универсальных хеш функций более продуктивным является применение слабо смещенных массивов.

2.6.3 Строго универсальное хеширование на основе слабосмещенных массивов.

Слабо смещённые массивы впервые были рассмотрены в работах [] для массивов дискретных значений большой размерности с распределением незначительно отличающимся от равномерного. Слабо смещённые массивы определяют свойства распределений хешей в столбцах массива [].

Пусть -массив, содержащийстрок,столбцов и записи из набораэлементов и. Массивявляется-смещённым (-biased), если любая нетривиальная линейная комбинация столбцов имеет смещение . Смещение вектораопределяется как

,

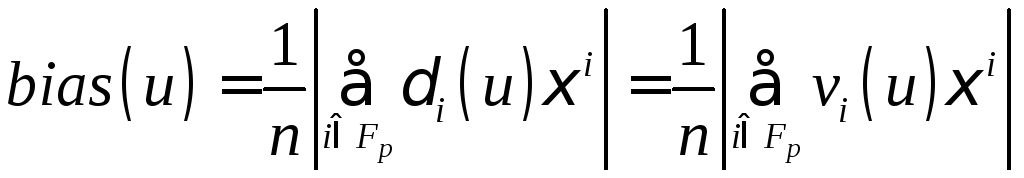где есть частота появления элементав последовательности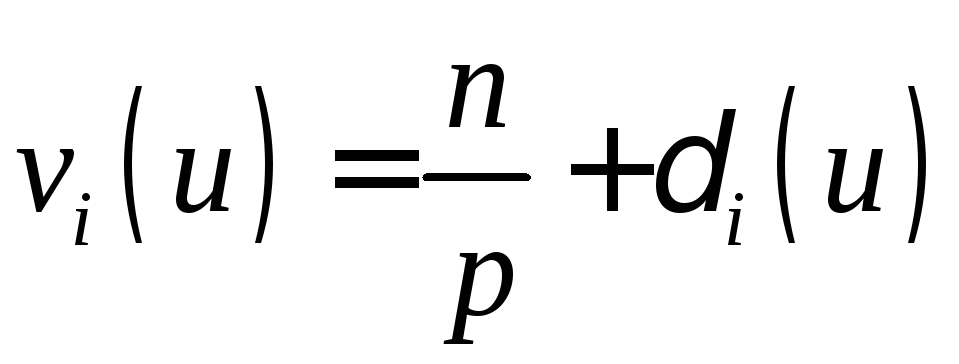_, ,- есть отклонение частотыот среднего значения и,комплексный корень- степени из единицы

Замечание 2.8.

1. Смещение массива является свойством - линейного кода, построенного с помощью столбцов порождающей матрицы.

2. Для двоичных массивов параметр смещения прямо связывается с вероятностями появления 0 и 1 в столбцах массива.

3. Для строго универсального класса, массив хеш значений определяется массивом со смещением равным нулю [55].

Практическим методам построения слабосмещенных массивов является метод сумм экспонент Вейля- Карлитца- Ушиямы (ВКУ).

Метод сумм экспонент ВКУ определяет массив со смещением , с записями вида , где - базис поля│,ине кратно,- след элемента.

Массив аутентификаторов является почти строго универсальным , если каждый столбец имеет смещение 0 и для двух записейодной строки в любых столбцахусловнаявероятность и равномерном распределении номера строка[54]. Строка массива определяется значением ключа, столбец - сообщением источника и значение записи является аутентификационным тегом.

Замечание 2.9.

1. Универсальное хеширование определяется через слабосмещённые массивы, является обобщением конструкций линейных кодов, ВКУ массивов.

2. Построение аутентификации определяется тем, что используется специальное индексирование строк массива аутентификаторов и записей, что увеличивает пространство ключей и записей, и приводит к лучшим оценкам параметров аутентификации.