
1.4. Устойчивость рыночного равновесия в концепции л. Вальраса и а. Маршалла.
В состоянии равновесия цена и объем товара заданы уравнениями спроса и предложения, точкой пересечения кривых спроса и предложения. При изучении устойчивости равновесия процессы рассматриваются в динамике.
На рынке установилась цена, обеспечивающая равновесие, и при ней поглощается все предложение товара. Любое возмущение (использование запасов как производителями, так и покупателями; запаздывание со стороны спроса или предложения и т.п.) приводит к тому, что на рынке устанавливается другая цена. Возникает вопрос, будет ли движение цены во времени после возмущения направлено к исходному положению равновесия или к другому равновесию, и сколь быстро будет происходить процесс приспособления. Так, слишком большое начальное возмущение может качнуть всю систему из одного положения равновесия к другому, может существовать несколько цен равновесия.
Возникающие возмущения по разному влияют на динамику экономической системы, поэтому проблема устойчивости разрешается не единственным образом. Равновесие может быть устойчивым в одних динамических условиях, и неустойчивым – в других.
Рассмотрим
лишь небольшие отклонения от положения
равновесия. Поэтому спрос и предложение
являются линейными функциями. Таким
образом,
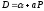 ;
;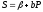 ,
,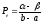 ,
,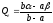 .
Постоянные
.
Постоянные и
и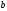 характеризуют наклоны кривых спроса и
предложения в точке равновесия:
характеризуют наклоны кривых спроса и
предложения в точке равновесия: величина
величина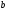 может быть положительной и отрицательной.
может быть положительной и отрицательной.
Концепция
устойчивости равновесия по Л. Вальрасу
состоит в
следующем. Цена установилась слишком
низкой, спрос больше предложения и цена
повышается до тех пор, пока не будет
достигнуто равновесие. Допустим, что
скорость повышения цены пропорциональна
размерам дефицита. Чем больше спрос
превосходит предложение, тем быстрее
растет цена. Уменьшение запасов на
стороне предложения будет вести систему
к состоянию равновесия. Поэтому
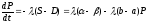 .
Под
.
Под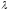 понимается скорость реакции цены на
дефицит. Чем больше
понимается скорость реакции цены на
дефицит. Чем больше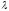 ,
тем быстрее цена реагирует на дефицит
предложения.
,
тем быстрее цена реагирует на дефицит
предложения.
Используем
решение, полученное в модели 3:
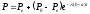 .
Цена
.
Цена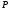 равномерно и монотонно стремится к
равномерно и монотонно стремится к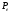 ,
если
,
если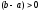 положительно (множитель
положительно (множитель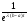 стремится
стремится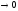 при
при ).
В таком случае равновесие устойчиво и
).
В таком случае равновесие устойчиво и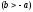 .
Цена
.
Цена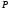 монотонно удаляется от
монотонно удаляется от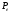 ,
если
,
если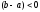 ,
т.е.
,
т.е.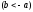 и тогда равновесие неустойчиво.
и тогда равновесие неустойчиво.
Концепция
устойчивости равновесия по А. Маршаллу.
Если в
какой-то момент времени объем предложения
отличается от равновесного уровня
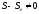 ,
то ожидаемые цены, которые готовы
заплатить покупатели, отличаются от
цен, приемлемых для продавца. Построим
динамическую модель, в которой объем
предложения увеличивается, если цены
продавцов ниже тех, которые предлагают
покупатели. Исходные условия:
,
то ожидаемые цены, которые готовы
заплатить покупатели, отличаются от
цен, приемлемых для продавца. Построим
динамическую модель, в которой объем
предложения увеличивается, если цены
продавцов ниже тех, которые предлагают
покупатели. Исходные условия: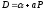 ,
,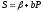 ,
цена спроса
,
цена спроса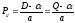 ,
цена предложения
,
цена предложения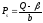 .
Скорость увеличения предложения
пропорциональна разности – цена продавца
минус цена покупателя
.
Скорость увеличения предложения
пропорциональна разности – цена продавца
минус цена покупателя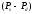 .
Тогда
.
Тогда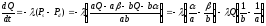 .
Следовательно, для любой точки имеет
место равенство:
.
Следовательно, для любой точки имеет
место равенство:
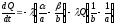 .
(1.9)
.
(1.9)
Для точки равновесия
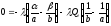 (1.10)
(1.10)
Из (1.9) вычитаем (1.10), получим:
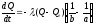 .
(1.11)
.
(1.11)
Обозначим
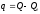 .
Тогда
.
Тогда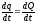 .
Уравнение (1.11) приобретает вид:
.
Уравнение (1.11) приобретает вид: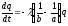 ,
или
,
или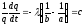 .
Отсюда
.
Отсюда .
Решение дифференциального уравнения:
.
Решение дифференциального уравнения: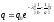 .
Возвращаясь к исходным обозначениям,
решение имеет вид:
.
Возвращаясь к исходным обозначениям,
решение имеет вид:
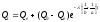 .
(1.12)
.
(1.12)
Решение (1.12) позволяет сделать следующие выводы:
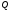 монотонно
стремится к
монотонно
стремится к
 ,
если
,
если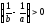 и равновесие устойчиво;
и равновесие устойчиво;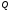 монотонно удаляется от
монотонно удаляется от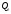 ,
если
,
если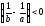 и равновесие неустойчиво.
и равновесие неустойчиво.
Таким образом, в зависимости от наклона кривых спроса и предложения имеются возможности:
Если
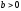 ,
,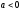 ,
то
,
то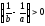 ,
,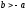 и равновесие устойчиво.
и равновесие устойчиво.Если
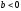 ,
,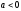 ,
то если
,
то если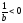 ,
,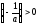 ,
разность
,
разность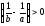 и при
и при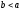 равновесие устойчиво.
равновесие устойчиво.Если
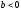 ,
,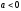 ,
разность
,
разность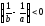 ,
,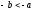 ,
равновесие неустойчиво
,
равновесие неустойчиво
Таким
образом, при
 ,
,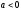 равновесие устойчиво и по Л. Вальрасу
и по А. Маршаллу, если
равновесие устойчиво и по Л. Вальрасу
и по А. Маршаллу, если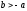 .
.
Заключение по разделу
В разделе построена паутинообразная модель рынка одного товара, проанализированная в дискретном и непрерывном анализе;
выведена зависимость цены от определяющих ее параметров, позволяющая определить ее величину в любой отрезок (момент) времени;
исследованы условия достижения на рынке состояния равновесия;
рассмотрены процессы достижения равновесия на рынке, равномерные колебания, взрывное колебание;
построена модель, учитывающая наличие запасов на рынке;
проанализированы условия устойчивого и неустойчивого равновесия в концепции Л. Вальраса и А. Маршалла.
Проектное задание: на основе лекции преподавателя и рекомендуемой литературы изучить паутинообразную модель рынка одного товара в дискретном и непрерывном анализе, модель в включением запасов, а также устойчивость равновесия. Применить полученные знания в решении задач рубежного контроля.
Контрольные вопросы
1. Проиллюстрируйте графически паутинообразную модель рынка одного товара в случае отставания предложения от спроса.
2. Представьте графически движение рынка к точке равновесия в редком случае, когда линейные функции спроса и предложения имеют одинаковый наклон – положительный и отрицательный.
3. Используя линейные функции спроса и предложения, покажите, как изменяется цена в любой период времени.
4. Объясните, при каком условии рынок приходит в состояние равновесия.
5. Что собой представляет взрывное колебание цены и какой параметр его вызывает?
Поясните смысл устойчивости равновесия на примере паутинообразной модели.
Какое практическое применение имеет паутинообразная модель рынка одного товара для производителя?
Поясните различие в концепции устойчивости равновесия у Л. Вальраса и А. Маршалла и объясните, почему устойчивость достигается при одном и том же условии в концепциях обоих экономистов.
Задания рубежного контроля
1.
Используя функции спроса и предложения
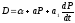 ;
;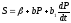 ,
сделайте обобщение - определите цену и
объем производства в паутинообразной
модели рынка одного товара.
,
сделайте обобщение - определите цену и
объем производства в паутинообразной
модели рынка одного товара.
2.
В дискретной модели выразить
 и
и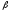 через
через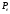 и
и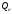 .
Каков экономический смысл параметров
.
Каков экономический смысл параметров и
и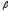 в этой модели? Если
в этой модели? Если
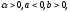 то каковы пределы изменения величины?
то каковы пределы изменения величины?
3.
В паутинообразной модели выразить
 и
и
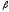 через равновесные значения цены
через равновесные значения цены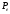 и
объема
и
объема
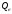 .
Каков
экономический смысл параметров
.
Каков
экономический смысл параметров
 и
и
 ?
Если
?
Если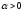 ,
,
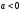 ,
,
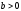 ,
то
каковы будут пределы изменения величины
,
то
каковы будут пределы изменения величины
 ?
?
4.
Равновесие на рынке описывается следующей
паутинообразной моделью:
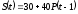 ,
,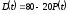 ,
где
,
где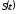 -
предложение,
-
предложение,
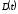 - спрос,
- спрос,
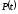 -
цена равновесия,
-
цена равновесия,
 -
период
времени. Определить, насколько процентов
изменилась равновесная цена за последнее
колебание, если
-
период
времени. Определить, насколько процентов
изменилась равновесная цена за последнее
колебание, если
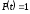 .
.
5.
Показать, что если
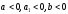 ,
то в непрерывной паутинообразной модели
существуют две возможности для
,
то в непрерывной паутинообразной модели
существуют две возможности для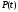 :
:
-
если
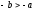 ,
то
,
то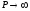 монотонно,
монотонно,
-
если
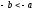 ,
то
,
то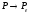 .
Дать графическую интерпретацию
полученному результату.
.
Дать графическую интерпретацию
полученному результату.
6.
Регулярные линейные сдвиги во времени
кривых спроса и предложения характеризуются
уравнениями:
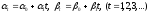 .
Существуют ли для цены решение типа
.
Существуют ли для цены решение типа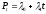 ,
т.е. регулярный прямолинейный рост во
времени?
,
т.е. регулярный прямолинейный рост во
времени?
7.
Построить динамическую модель 3,
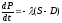 ,
для функций спроса
,
для функций спроса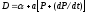 и предложения
и предложения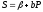 .
.
Литература
1. Аллен Р. Математическая экономия. М.: ИЛ. 1963. Гл. 1
2. Гальперин В.М., Игнатьев С.М., Моргунов В.И. Микроэкономика. С-Пб. Экономическая школа. Т.1. 1998. Гл. 2. С. 63
3. Баумоль У. Экономическая теория и исследование операций. М.: Прогресс, 1965. Гл. 8.
Воркуев Б.Л. Модели микроэкономики. М.: ТЕИС, 2002. Гл. 1.
5. Германова О.Е., Черкасова Т.П. Математические модели в экономике. Учебное пособие. Ростов н/Д. Изд-во СКАГС. 2007.
Вэриан Хэл Р. Микроэкономика. Промежуточный уровень. Современный подход. М.: ЮНИТИ, 1997. Гл.1.
Гребенников П.И., Леусский А.И., Тарасевич Л.С. Микроэкономика. СПб.: Из-во СПб университета экономики и финансов, 1997. Введение. Гл. 3.
Иванилов Ю.П., Лотов А.В. Математические модели в экономике. М: Наука, 1979. С. 19-28.
Ланге О. Введение в эконометрику. М.: Прогресс, 1964. Гл. 2.
Чеканский А.Н., Фролова Н.Л. Микроэкономика. Промежуточный уровень: Учебник. М.: ИНФРА-М, 2005. Разд. 1. Гл. 6.
