Модуль 1	Предпочтения и выбор потребителя
Тема 2	Оптимальное положение потребителя в экономике
2.1	Необходимое и достаточное условия решения неоклассической задачи потребления
2.2	Экономико-математическая модель выбора потребителя. Основное уравнение теории ценности.
2.3	Предельная полезность по доходу и предельная полезность по цене продукта (тождество Роя)
2.4	Предельный расход по полезности и предельный расход по цене продукта (лемма Шепарда)

Тема 1. Оптимальное положение потребителя в экономике

2.1. Необходимое и достаточное условия решения неоклассической задачи потребления

Одним из субъектов в рыночной экономике является домашнее хозяйство, распределяющее свой доход на покупку товаров и услуг. Рациональное ведение хозяйства сводится к решению задачи, какое количество товаров и услуг необходимо приобрести при данном доходе и уровне цен для наиболее полного удовлетворения потребностей.

В экономике производится товаров,

и потребитель приобретает набор

,

в котором - количествого блага, приобретаемого потребителем,

В анализе поведения потребителя используются следующие аксиомы. Товары обладают свойством делимости и их объем может изменяться на бесконечно малую величину. Выбор потребителя в определенной мере завит от вкусов потребителя. Товары для потребителя или равноценны и безразличны или существует строгое предпочтение одного товара другому. Транзитивность характеризует непротиворечивость предпочтений потребителя, их рефлексивность и симметричность. Отношение предпочтения непрерывно. Это означает, что существует непрерывная действительная функция полезности . Если известна функция полезности, то ею является любая монотонно строго возрастающая функция, построенная на основе известной функции:, и другие.

Аксиома ненасыщения утверждает, что если функция полезности дифференцируема, то все первые частные производные функции – предельные полезности товаров положительны () >0. При увеличении потребления одного из товаров при неизменном потреблении всех остальных товаров, полезность набора увеличивается.

Аксиома строгой выпуклости (кривой безразличия) означает, что если наборы _͂ безразличны для потребителя, то при набор

_͂ . Если последнее условие выполняется для любых двух наборов, то кривая безразличия является строго выпуклой относительно начала координат.

Если функция полезности является дважды дифференцируемой и имеет непрерывные вторые частные производные , то их отрицательные значения отражают тот факт, что предельная полезность любого товара уменьшается по мере того, как увеличивается его потребление. Матрица Гессе, состоящая из вторых частных производных функции полезности по всем переменным отрицательно определена.

В неоклассической задаче потребитель выбирает набор товаров и услуг из допустимого множества наборов, который является наиболее предпочтительным при заданной функции полезности и бюджетном ограничении. Доход потребителя и цены товаровявляются заданными положительными параметрами. Денежные расходы на все товары и услуги не могут превышать денежные доходы потребителя. Условия задачи: дана функция полезности, бюджетное ограничение , , где Определить набор, имеющий максимальную полезность для потребителя.

Необходимым и достаточным условиями решения неоклассической задачи потребления являются условия Куна-Таккера для функции Лагранжа:

, (1.1)

где - множитель Лагранжа. Запишем условия Куна-Таккера:

. (1.2)

Предельная полезность товаров представлена величинойСистема уравнений имеет решение. Если, тогда . Поэтому для всех закупленных товаровмножитель Лагранжа положителен. Отношение предельной полезности товаров к их цене одинаково для всех товаров в наборе, а весь доход должен быть израсходован. Условия (1.2) принимают вид:

.

Условия (1.2) выполняются в точке и являются решением задачи потребления. Предельная полезность каждого товара равна нулю и, следовательно, общая полезность набора максимальна. Таким образом определяем спрос на товары как функции цен и доходаЭто функции спроса потребителя по Маршаллу (по Вальрасу). Функции спроса являются однородными нулевой степени, что следует из уравнения бюджетной линии.

Определить характер функциональной зависимости спроса потребителя на товары при изменении цен и дохода можно, проведя сравнительно-статистический анализ – сопоставив параметры оптимума потребителя до и после изменения одной из названных переменных. Так можно вывести зависимости «доход – потребление» и «цена – потребление».

Оптимальный множитель Лагранжа, равный отношению предельной полезности любого товара к его цене, интерпретируется как полезность, приходящаяся на денежную единицу, измеряет предельную полезность денежной единицы. Поскольку числитель выражения - предельная полезность единицы товара, а знаменатель его предельные издержки, то множитель Лагранжа можно представить как коэффициент «результат - затраты», который одинаков для всех товаров, входящих в набор, в оптимальной точке. Его можно рассматривать как меру степени, в которой изменение бюджетного ограничения влияет на значение функции полезности. При высокомдополнительная денежная единица в доходе потребителя существенно увеличивает общую полезность набора, при низком коэффициенте увеличивает незначительно.Согласно необходимым условиям максимума функции полезности в оптимальной точке каждый рубль, дополнительно затрачиваемый на покупку товара, должен приносить покупателю одинаковую «добавочную полезность» не зависимо от того, на какой товар он был потрачен. Множитель является функцией цен и доходаи представляет величину, на которую увеличится оптимальный уровень полезности набора при бесконечно малом приращении дохода.

Пропорциональное изменение цен всех товаров и дохода не изменяет содержание оптимального набора потребителя. Функции спроса являются однородными относительно всех цен и дохода. Поэтому спрос зависит от относительных цен и от отношения дохода к одной из цен.

В случае двух товаров функция Лагранжа имеет вид: (1.3)

решение должно удовлетворять системе уравнений: Решение системы уравнений определяет оптимальный набор, который отмечается точкой касания кривой безразличия и бюджетной линии. Точканазывается длинной точкой, точка без последней координаты, т.е.называется короткой точкой (рис. 1.1). Поскольку функция полезности обладает рядом свойств,_а то система уравнений имеет единственное решение.

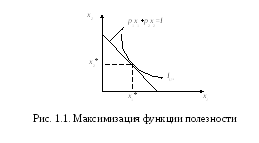
Наклон бюджетной линии равен . Поскольку во всех точках кривой безразличия полезность наборов одинакова, то наклон кривой безразличия в оптимальной точке находим из выраженияОтсюдаСледовательно наклоны бюджетной линии и кривой безразличия равны в оптимальной точке.

Функция называется косвенной (неявной) функцией параметроваесть максимум функции полезности. Максимальная полезность, достигаемая в точке оптимального набора, косвенно зависит от цен и дохода. Косвенная функция полезности обладает следующими свойствами.

Косвенная функция не возрастает по ценам. Если растут цены при постоянном доходе, то объемы спроса в оптимальном наборе уменьшаются. Если цена хотя бы одного товара строго возрастает, то общая полезность строго убывает. Данная функция строго возрастает по доходу при неизменных ценах. С ростом дохода увеличивается количество продуктов в оптимальном наборе потребителя. Функция является однородной функцией по всем одновременно изменяющимся переменным. Это означает, что если все переменные (цены всех товаров и доход потребителя) увеличиваются в илираз, то общая полезность приобретаемого набора не изменяется. Запишем это свойство для набора, состоящего из двух товаров: _. Для косвенная функция полезности является однородной нулевой степени. В отличие от кривых безразличия уровни косвенной функции полезности квазивыпуклы к началу координат. Поэтому, если при переходе от одной на другую более высокую кривую безразличия полезность набора увеличивается, то в случае косвенной функции полезности отображаемые ею уровни полезности нарастают в направлении не от начала координат, а в обратном направлении. Благодаря строгому изменению косвенной функции полезности по доходу (возрастанию или убыванию), она имеет обратную функцию - функцию расходов потребителя.

Так как цены товаров и доход потребителя положительны, то косвенная функция полезности непрерывна по всем переменным. Свойства косвенной функции полезности приводятся без доказательства.

Косвенная функция полезности применяется для изучения влияния налогов и субсидий на уровень полезности набора, приобретаемого потребителем. Ведь налоги уменьшают, а субсидии увеличивают доход потребителя.

Условия второго порядка или достаточные условия оптимизации состоят в следующем. Условие устойчивости или необходимое условие экстремума функции многих переменных имеет вид , так какТогда выполняется достаточное условие оптимальности: полный дифференциал второго порядка функции полезности Лагранжа отрицателенпри отрицательных значениях вторых частных производных функции полезности и

Следовательно, набор имеет максимальную общую полезность для потребителя.