Лабораторная работа № 8

ОПРЕДЕЛЕНИЕ ПОКАЗАТЕЛЯ ПРЕЛОМЛЕНИЯ И ДИСПЕРСИИ СТЕКЛЯННОЙ ПРИЗМЫ С ПОМОЩЬЮ СПЕКТРОСКОПА

Цель работы:Экспериментально определить величину дисперсии и коэффициент дисперсии стеклянной призмы; научиться работать со спектроскопом.

Оборудование:1. Спектроскоп двухтрубный.

2. Трубка заполненная водородом.

3. Катушка Румкорфа.

4. Выпрямитель ВС-4-12; РНШ; штатив.

Теория

Опыт показывает, что коэффициент преломления среды n зависит от длины световой волны λ, т.е. n есть функция λ

.

Явление зависимости коэффициента преломления n от λ называется дисперсией света, а функция ƒ(λ) характеризует дисперсионные свойства вещества. Следует подчеркнуть, что наличие дисперсии света явилось в свое время одним из фундаментальных затруднений первоначальной электромагнитной теории Максвелла.

Согласно теории Максвелла скорость света в веществе определяется соотношением

. (1)

А абсолютный показатель преломления среды:

. (2)

Сравнивая выражения (1) и (2) , получаем

. (3)

В теории Максвелла ε и μ, а следовательно, и n, рассматривались как постоянные величины, независящие от λ. Таким образом, явление дисперсии, т.е. факт зависимости n от λ, осталось неучтенным в теории Максвелла.

Эти затруднения электромагнитной теории Максвелла были устранены электронной теорией Лоренца, которая раскрыла микроскопический смысл макроскопических величин ε и μ и объяснила их зависимость от λ.

В 1666 году Ньютон впервые провел экспериментальные исследования дисперсии. Пропустив белый пучок света от щели через призму, преломляющее ребро которой параллельно щели и перпендикулярно плоскости рисунка, и проецируя изображение щели на экран, он получил изображение щели в виде цветной полосы (рис.1).

1 – источник света; 2 – конденсор; 3 – щель, расположенная перпенди-кулярно рисунку; 4 – объектив; 5 – призма, преломляющее ребро которой (А) параллельно щели; 6 – экран.

Если сравнивать спектры, полученные с помощью призм с равными преломляющими углами, но из разных веществ, можно заметить, что спектры не только отклонены на разные углы по отношению к белому изображению щели, но и растянуты на большую или меньшую ширину.

Количественной мерой дисперсии служит величина , котораяпоказывает, как быстро меняется коэффициент преломления n с изменением λ.

Для исследования дисперсионной способности призмы, т.е. функции, Ньютон в 1672 г. применил метод скрещенных призм (рис. 2.), который показал, что фиолетовые волны преломляются больше, чем красные.

Величина различна в разных областях спектра для одной и той же призмы. Она имеет большее значение для фиолетовых лучей (рис. 3), поэтому фиолетовая часть спектра более растянута. Различие в величинах дисперсии в разных частях спектра видно из различного наклона касательных к кривойк осиλ. Из рис. 3 следует, что

.

Такую зависимость показатель преломления n имеет для прозрачных сред (стекла, кварца) на всем протяжении видимого спектра (рис. 3). Эта зависимость называется нормальной дисперсией.

В 1862 году Леру наблюдал преломление в призме, наполненной парами йода, в котором при уменьшении длины волны λ уменьшался и показатель преломления паров йода n. Эту особенность Леру назвал ано-мальной дисперсией.

Систематические исследования Кундта, который использовал для этих наблюдений метод скрещенных призм, позволили установить закон, согласно которому явление аномальной дисперсии тесно связанно с поглощением света: все тела, дающие аномальную дисперсию в какой-либо области, сильно поглощают свет в этой области.

Опыт показывает, что все вещества поглощают свет в некоторой области спектра. Если эти области расположены в видимой части спектра, то вещество выглядит окрашенным. Излучение после поглощения имеет цвет окраски – дополнительный к поглощенному свету. Например, рубин поглощает в сине-зеленой области спектра. В то же время окраска рубина – красная. В области полосы поглощения функция имеет сущест-венно другой вид, чем вдали от этой полосы. Рассмотрим зависимости показателя преломления, представленные на рис. 4.

На участке (аb) показатель преломления уменьшается с ростом длины волны – нормальная дисперсия.

При приближении к области поглощения со стороны малых длин волн λпоказатель преломленияn с ростом длины волныλсначала очень быстро уменьшается (участокbс), достигая иногда значения меньше единицы. Затем, при переходе через полосу поглощения (участок сf), показатель преломления сильно возрастает, переходя через точкуO, и достигает максимального значения (точкаf). Вдали от полосы поглощения (участок fd), опять наблюдается нормальная дисперсия.

Поведение кривой вблизи полосы поглощения описывает явление аномальной дисперсии (на рис. 4 – участок сf), т.е. в этой области спектра показатель преломления растет с ростом длины волны.Аномальная дисперсия света в видимой области спектра наблюдается в тонких слоях сильных красителей (например, фуксин, цианин), а также в парах натрия и йода.

Надо отметить, что термин «аномальная дисперсия» не соответствует настоящему физическому смыслу и является неудачным. Он принят в силу исторических причин, так как впервые явление аномальной дисперсии было обнаружено только у одного вещества. В действительности аномальная дисперсия электромагнитных волн имеет место в любом веществе вблизи полосы поглощения, но эти полосы поглощения у прозрачных веществ лежат в невидимой для глаза области спектра. Например, у кварца – в инфракрасной, у стекла – в ультрафиолетовой.

В настоящей работе определение показателя преломления вещества основано на измерении угла наименьшего отклонения лучей призмой.

На рис. 5 показана преломляющая призма, где А – преломляющий угол призмы. Луч света идет по направлению В₁ВСС₁,δ – угол отклонения луча. Уголδбудет наименьшим, если

, (4)

поскольку луч внутри призмы идет параллельно основанию. Именно такой случай изображен на рис. 5.

По законам преломления получаем следующие равенства

, а .

Отсюда следует, что . (5)

Угол отклонения δ_min,являясь внешним углом треугольникаDBC, равен сумме двух внутренних углов, с ним не смежных:

.

Из соотношений (4) и (5) получаем

, (6)

. (7)

Здесь учтен тот факт, что рассматриваемые углы образованы взаимно перпендикулярными сторонами. С другой стороны, угол

, (8)

выглядит как и внешний угол треугольника ЕВС.

Из равенств (7) и (8) следует, что

.

Учитывая (5) получаем следующие равенства

; . (9)

Из равенств (6) и (9) получаем

или . (10)

Подставляя значения α₁ иβ₁из формул (9) и (10) в выражение

,

находим

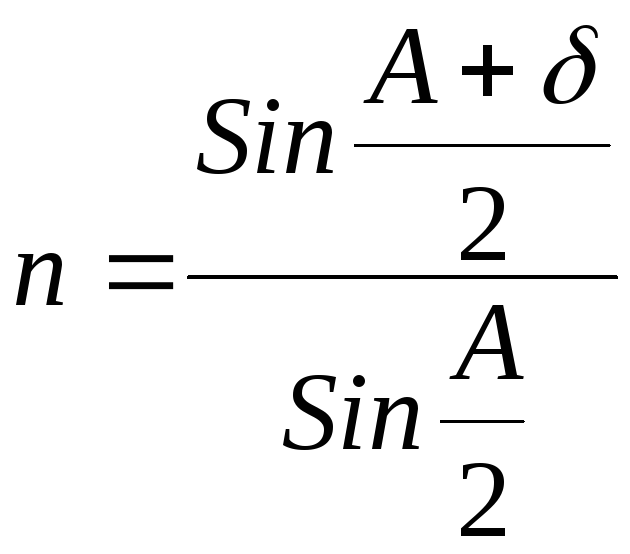. (11)

Из формулы (11) видим, что для определения показателя преломления вещества призмы нужно знать преломляющий угол призмы А и угол наименьшего отклонения .Именно этот вывод является теоретической основой выполнения данной работы.